Nous venons de voir qu'en fonction des systèmes optiques, l'image d'un point est soit exactement un point (tous les rayons issus d'un point convergent en un seul point image), ou soit une tache (tous les rayons ne convergent pas tous en un seul point, mais dans une petite zone).
 Stigmatisme
Stigmatisme
Lorsque, à travers un système optique, l'image de chaque point objet est un point, on dit que le système est rigoureusement stigmatique. On parle de stigmatisme approché si l'image d'un point est une petite tache. La notion de stigmatisme approché est assez subjective. Elle dépend également du récepteur utilisé pour voir l'image. On tolérera plus facilement un système avec un stigmatisme approché si le récepteur possède de gros pixels (surtout s'ils sont plus gros que la tache image) que s'il possède de petits pixels.
Poisson dans un aquarium : stigmatisme approché
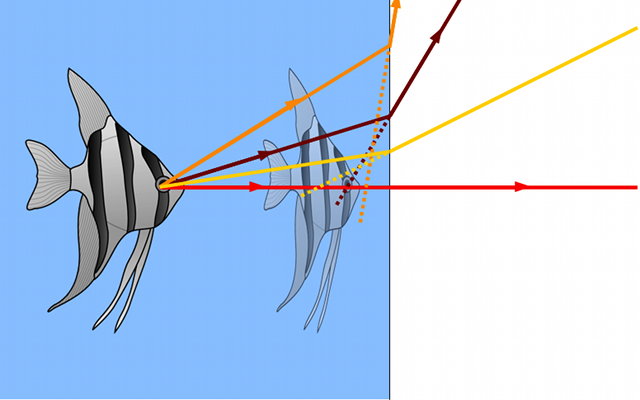
Si on trace plusieurs rayons issus d'un même point (l'oeil par exemple), tous ne convergent par au même point. L'image du poisson est floue ! Le stigmatisme ne peut être qu'approché.
Crédit :
ASM/B. Mollier
Bougie à travers un miroir : stigmatisme rigoureux
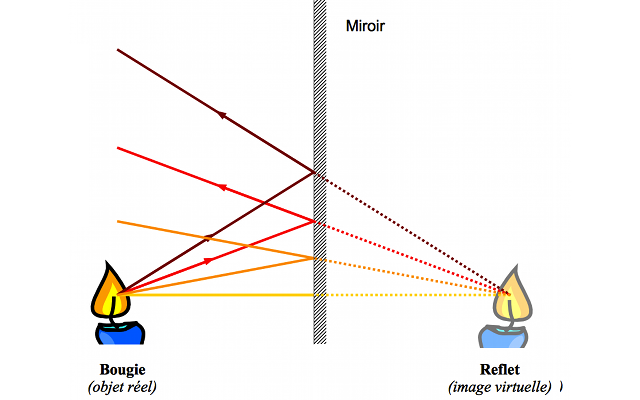
Dans le cas du miroir plan, tous les rayons issus d'un même point de l'objet convergent en un même point de l'image. Celle-ci sera nette. Le miroir plan est le seul système optique garantissant un stigmatisme rigoureux en tous points.
Crédit :
ASM/B. Mollier
Un système est dit aplanétique si l'image d'un objet perpendiculaire à l'axe optique (l'axe de symétrie du système) est elle aussi perpendiculaire à ce dernier.
Cette définition ne vous parle pas pour l'instant, mais elle prendra tout son sens au chapitre suivant.
Aplanétisme
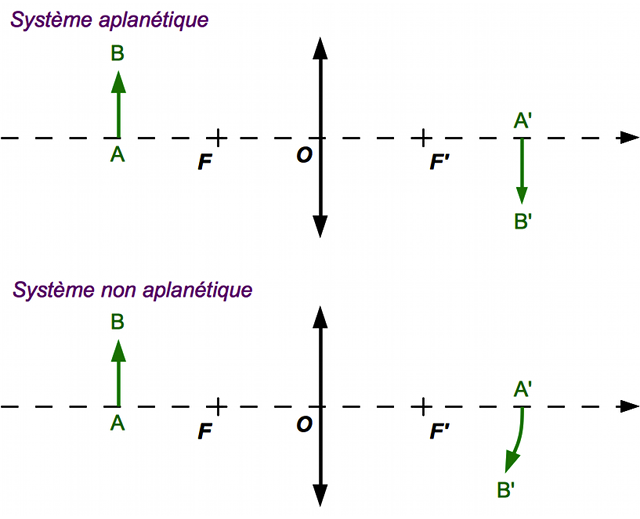
L'objet
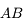
est perpendiculaire à l'axe optique. Dans le cas du haut, l'image
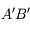
est elle aussi perpendiculaire à l'axe optique, le système est aplanétique. Dans le cas du bas, elle n'est pas perpendiculaire à l'axe, elle est tordue. Le système n'est pas aplanétique.
Crédit :
ASM/B. Mollier
 Mise en évidence
Mise en évidence
Soit un faisceau de lumière constitué de plusieurs rayons lumineux. Si on les fait traverser une lentille, on constate qu'ils convergent. Ils convergent, certes, mais pas tous au même point. Nous ne sommes pas en condition de stigmatisme rigoureux.
Si on diaphragme le faisceau lumineux, c'est-à-dire si on l'ampute de ses rayons extérieurs, on constate que la condition de stigmatisme est beaucoup mieux respectée.
Nous venons de mettre en évidence les conditions de Gauss.
 Conditions de Gauss
Conditions de Gauss
Les conditions de Gauss, ou l'approximation de Gauss, sont obtenues lorsque les rayons lumineux possèdent un angle d'incidence très faible par rapport à l'axe optique, et en sont peu éloignés. Ils sont dits paraxiaux.
Conditions de Gauss
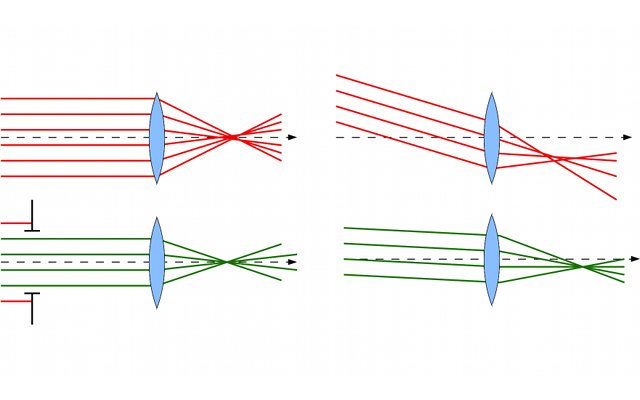
Dans les conditions de Gauss, les rayons sont proches de l'axe optique (en bas à gauche) et peu inclinés (en bas à droite).
Crédit :
ASM/B. Mollier
Dans ces conditions, les conditions de stigmatisme et d'aplanétisme sont en général respectées.
Pour les obtenir, il suffit en général de placer un fort diaphragme en entrée du système.
 Remarques
Remarques
Dans les chapitres suivants, nous nous placerons dans ces conditions.
Si ces conditions permettent d'obtenir un bon stigmatisme et aplanétisme, elles ne sont en général pas recherchées par les opticiens. Le grand inconvénient de ces conditions est qu'à cause du diaphragme, on obtient peu de lumière et un champ de vue très restreint. C'est le contraire que l'on recherche en astronomie et en photographie. Toute la difficulté consiste donc à corriger toutes les aberrations optiques pour retrouver du stigmatisme et de l'aplanétisme. C'est pour cela qu'il y a tant de lentilles (une dizaine) dans un simple objectif photo.
 Stigmatisme
Stigmatisme


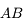 est perpendiculaire à l'axe optique. Dans le cas du haut, l'image
est perpendiculaire à l'axe optique. Dans le cas du haut, l'image 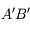 est elle aussi perpendiculaire à l'axe optique, le système est aplanétique. Dans le cas du bas, elle n'est pas perpendiculaire à l'axe, elle est tordue. Le système n'est pas aplanétique.
est elle aussi perpendiculaire à l'axe optique, le système est aplanétique. Dans le cas du bas, elle n'est pas perpendiculaire à l'axe, elle est tordue. Le système n'est pas aplanétique.
