Quelques notions d'optique de base sont rappelées, afin de comprendre dans les grandes lignes les principes instrumentaux les plus couramment mis en oeuvre pour acquérir une image en astronomie.

Quelques notions d'optique de base sont rappelées, afin de comprendre dans les grandes lignes les principes instrumentaux les plus couramment mis en oeuvre pour acquérir une image en astronomie.



Les images de grands champs stellaires sont typiquement obtenues par observation au foyer primaire d'un télescope, càd au foyer du miroir primaire collecteur de photons.
Pour en savoir plus : projet MEGACAM du télescope CFH
Optique géométrique : vocabulaire de l'optique géométrique, image d'un objet à l'infini.
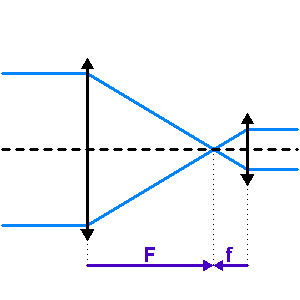
Formation d'image au foyer primaire d'un télescope.
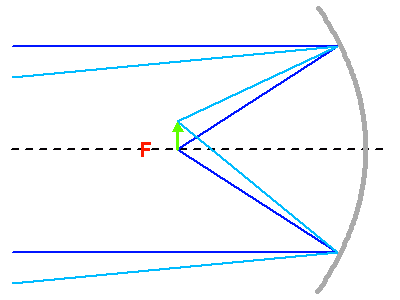
Le collecteur de photons le plus couramment utilisé est le miroir parabolique, qui convertit après réflection une onde plane en une onde sphérique convergente. Un miroir parabolique conjugue ainsi les sources de lumière situées à l'infini au foyer de la parabole. Un tel collecteur est équivalent à une lentille de diamètre et focale identique. Une lentille fonctionne en transmission et non en réflexion comme un miroir, mais le principe de fonctionnement est le même. Une lentille transforme une onde plane en onde sphérique, et concentre ainsi la lumière provenant d'une étoile lointaine située sur son axe optique en son foyer.
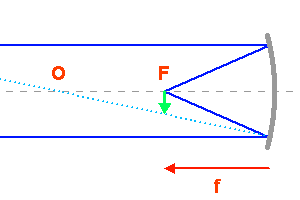
Un objet à l'infini, s'il est résolu, se caractérise par une taille angulaire
 . Au foyer du miroir primaire du télescope, cet objet donne une image de taille linéaire
. Au foyer du miroir primaire du télescope, cet objet donne une image de taille linéaire 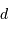 telle que
telle que 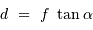 , avec
, avec 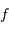 la focale du collecteur. L'angle
la focale du collecteur. L'angle 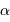 est le plus souvent très petit, et donc confondu avec sa tangente. On garde, avec
est le plus souvent très petit, et donc confondu avec sa tangente. On garde, avec 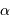 compté en radian :
compté en radian :
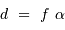
L'analogie avec une lentille est directe.
Tous les systèmes optiques donnant une image réelle d'un objet réel peuvent se résumer en un système comprenant une seule lentille, équivalant au système entier. Dans le cas de l'observation astronomique où, mis à part l'observation in situ apportée par les atterrisseurs des sondes planétaires, l'objet est à l'infini, l'observation a donc lieu au foyer image de cette lentille équivalente.

Localisation du foyer primaire, et donnée de quelques éléments d'un télescope en monture équatoriale.
La parabole a pour propriété de ramener l'ensemble des rayons lumineux en provenance d'une source située à l'infini sur son axe optique (l'onde incidente est alors plane) en un même point : son foyer. On parle alors de conjugaison optique entre le foyer de la parabole et l'infini.
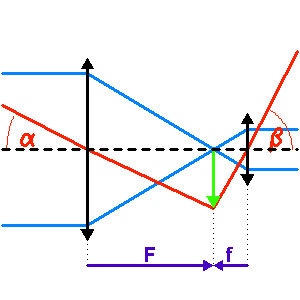
Ceci n'est en fait rigoureusement vrai que pour un rayon incident parallèle à l'axe de la parabole. Un faisceau de rayons parallèles inclinés sur l'axe optique ne va pas converger en un foyer unique, ce qui conduit à l'aberration de sphéricité : le plan focal est en fait incurvé.
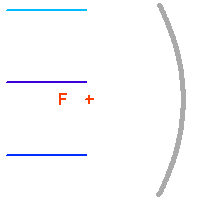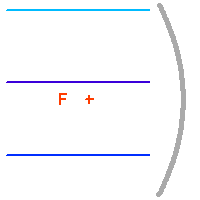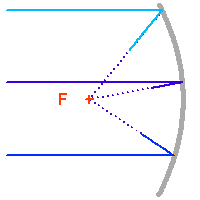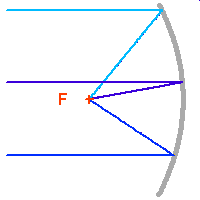

L'appliquette ci-jointe montre comment déterminer la lentille simple équivalente à un montage optique recueillant un faisceau provenant de l'infini. Elle se situe à l'intersection des rayons incidents d'une part, et convergeant vers le détecteur d'autre part.

L'appliquette ci-jointe rappelle, si besoin est, les règles pour localiser l'image par une lentille d'un objet à distance finie.
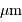 , au foyer d'un télescope de 12 m de focale ?
, au foyer d'un télescope de 12 m de focale ?
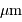 couvre sur le ciel un champ de 0.1". En déduire la focale du collecteur
couvre sur le ciel un champ de 0.1". En déduire la focale du collecteur
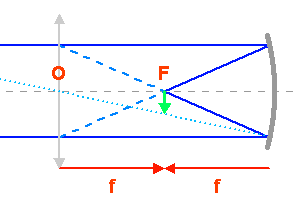
Image d'un objet à l'infini, image d'un objet au foyer.
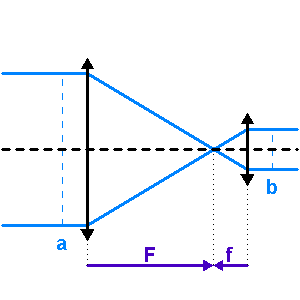
L'étude d'un montage optique particulièrement utile en astronomie, le montage afocal, montre que la taille angulaire du champ sur le ciel (champ objet) et le diamètre du faisceau lumineux en sortie de l'instrument sont liés de façon simple au grossissement du système.
Que ce soit pour observer à l'oeil nu, ou pour alimenter un spectromètre, le collecteur a pour fonction de transformer un faisceau à l'infini en un autre faisceau à l'infini.
L'objectif (la lentille ou le miroir côté objet) forme de l'objet à l'infini une image au foyer. L'oculaire (si le détecteur est l'oeil) ou l'optique de chambre permet de regarder cet objet à l'infini.
L'association de 2 optiques, l'objectif (côté objet) et l'oculaire (côté oeil) de foyer commun, transforme un faisceau parallèle en un autre faisceau parallèle.
Les focales équivalentes de l'objectif et de l'oculaire étant respectivement 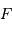 et
et 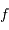 , le grossissement du faisceau, égal au rapport des tailles angulaires des image et objet
, le grossissement du faisceau, égal au rapport des tailles angulaires des image et objet 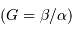 , vaut en valeur absolue :
, vaut en valeur absolue :
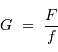
En effet, l'image intermédiaire au foyer commun a pour taille linéaire 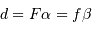 .
.
Les focales équivalentes de l'objectif et de l'oculaire étant respectivement 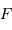 et
et 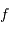 , le rapport des tailles du faisceau en entrée et en sortie vaut, en valeur absolue :
, le rapport des tailles du faisceau en entrée et en sortie vaut, en valeur absolue :
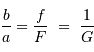
En effet, l'inclinaison du faisceau entre les foyers s'écrit, dans l'hypothèse des petits angles (pour laquelle 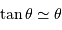 ) :
) : 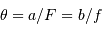 .
.
Le diamètre du faisceau en sortie est d'autant plus important que le champ objet est grand.
De ce qui précède, on déduit qu'en sortie d'un montage afocal, une instrumentation de taille réduite (dimensionnée par 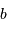 ) va nécessiter un grossissement élevé, et donc ne pourra porter que sur un champ objet de taille restreinte.
) va nécessiter un grossissement élevé, et donc ne pourra porter que sur un champ objet de taille restreinte.
La notion d'étendue de faisceau généralise cette idée.
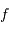 du secondaire est courte, plus le
grossissement est :
du secondaire est courte, plus le
grossissement est :



Viser un objet, c'est arriver à positionner précisément un collecteur et son instrument d'analyse. Ensuite, selon les objectifs scientifiques, on s'intéresse à un champ plus ou moins grand. La taille du champ est reliée aux propriétés du collecteur et de l'instrumentation.

L'angle d'ouverture d'un collecteur de lumière mesure le rapport entre le diamètre du collecteur et la focale résultante. Les instruments anciens et les lunettes présentent des angles d'ouverture fermés : le tube focal, de longueur très voisine de la focale résultante, est long et grand devant le diamètre collecteur. Les collecteurs récents et/ou de grand diamètre présentent de grands angles d'ouverture, pour limiter leur longueur. Il en est de même des antennes submillimétriques.

L'observation sur un grand champ nécessite un grand détecteur. Ceci est aujourd'hui réalisé par la juxtaposition de plusieurs détecteurs bidimensionnels de lumière comme les CCD ou les CMOS.
Optique géométrique
Former une image dans de 'bonnes' conditions nécessite de bien dimensionner une optique ; le champ est l'une des grandeurs importantes à considérer. Il dépend des propriétés d'ouverture du collecteur.
Un télescope se caractérise par sa focale résultante 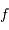 et par le diamètre
et par le diamètre 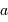 du collecteur.
du collecteur.
L'angle d'ouverture d'un instrument est le rapport entre le diamètre et la focale résultante, soit, avec les notations proposées, 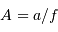 .
.
Le nombre d'ouverture d'un télescope est le rapport inverse.
Comme en photographie, on parle d'un instrument ouvert à 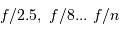 avec respectivement les nombres d'ouverture
avec respectivement les nombres d'ouverture 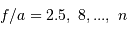 .
.
Exemples typiques d'ouverture : de 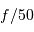 à
à 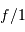 .
.
Plus le nombre d'ouverture est petit, plus le télescope est ouvert (grand angle d'ouverture) et admet des rayons de grande inclinaison. Un petit nombre d'ouverture correspond à une courte focale, ou à un grand diamètre.
Les télescopes les plus récents (télescopes optiques, radiotélescopes), de par leur grand diamètre collecteur, sont en général très ouverts, afin de limiter la longueur de leur focale, et donc leur encombrement.
Le champ objet est la région du ciel effectivement observée dans de bonnes conditions (stigmatisme suffisant pour la qualité d'image requise ; éclairement du champ uniforme, sans vignetage). Son extension dépend du collecteur, et de l'instrumentation et de son grossissement.
Avec 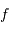 la focale résultante d'un collecteur et
la focale résultante d'un collecteur et 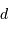 la taille du détecteur effectivement éclairée, le champ objet
la taille du détecteur effectivement éclairée, le champ objet 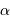 s'écrit simplement (dans l'approximation des petits angles) :
s'écrit simplement (dans l'approximation des petits angles) :
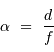
Comme l'angle d'ouverture, le champ objet décroît si la focale 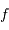 du télescope augmente.
du télescope augmente.
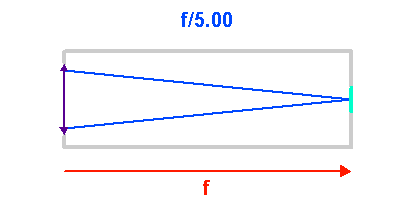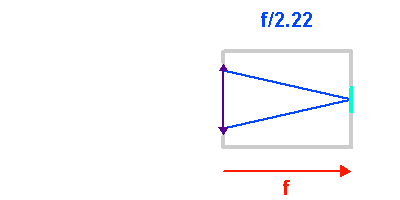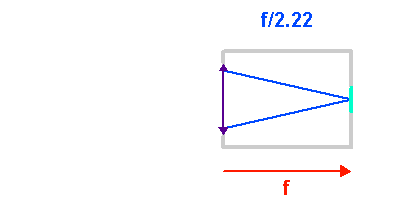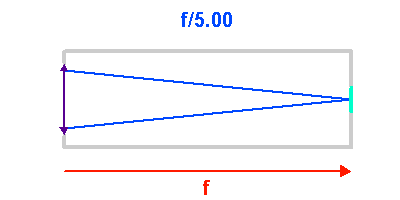
L'animation illustre comment l'ouverture géométrique d'un télescope varie avec la focale d'un collecteur. Plus le télescope est ouvert, plus l'inclinaison des rayons dans le télescope est importante.
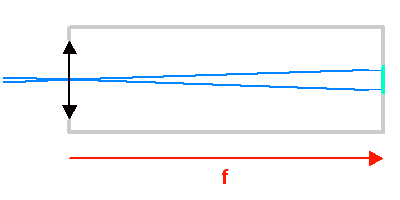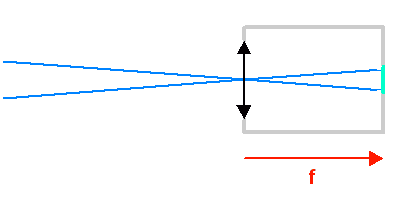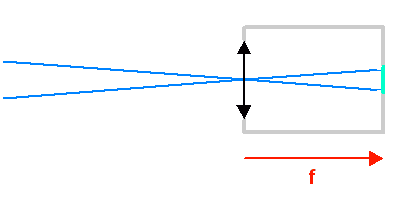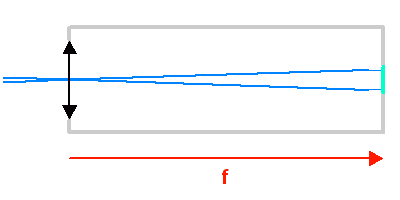
L'animation illustre comment la taille du champ objet varie avec la focale du collecteur.
Les données de l'appliquette ci-jointe reportent les mesures effectuées par un groupe d'étudiants observant au télescope de 60 cm du campus de Meudon de l'Observatoire de Paris. Le but de l'observation, premier contact avec le télescope, consiste à prendre conscience que le champ accessible au pointage est restreint, et qu'il est nécessaire pour pouvoir pointer un objet de garantir une précision angulaire, exprimée en seconde de temps et non d'angle, meilleure que 30 s.
Traversée du champ 
L'entraînement du télescope étant arrêté, les étoiles défilent dans le champ : les durées T1 et T2 mesurent la traversée du diamètre du champ par des étoiles brillantes, pour deux grossissements différents.
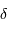 est proportionnelle à
est proportionnelle à 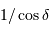
Difficulté : ☆ Temps : 10 min
Déterminer la focale équivalente d'un télescope de diamètre
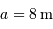 ouvert à f/3.75.
ouvert à f/3.75.
L'image est formée sur une matrice CCD de 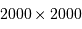 pixels, avec des pixels carrés de côté
pixels, avec des pixels carrés de côté 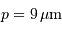 .
Quel champ voit un pixel ? Déterminer le champ de vue total dans
le ciel.
.
Quel champ voit un pixel ? Déterminer le champ de vue total dans
le ciel.
Difficulté : ☆ Temps : 20 min
Le télescope T60, installé sur la table équatoriale du campus de
Meudon de l'Observatoire de Paris, présente un miroir primaire de
diamètre 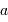 =60 cm.
=60 cm.
Déterminer son nombre d'ouverture, sachant que sa focale résultante vaut F = 9 m.
Quel grossissement est obtenu avec des oculaires de distance focale 45 ou 30 mm ?
L'ouverture du faisceau image étant de toutes façons inférieure au champ de vision de l'oeil (environ 60 degrés), déterminer le diamètre maximal du champ objet pour un oculaire de focale 45 ou 30 mm.
Difficulté : ☆☆ Temps : 30 min
Cet exercice s'appuie sur les données de l'appliquette "mesure du champ". Il est préférable d'avoir auparavant traité la section Systèmes de coordonnées .
Montrer par un schéma qu'une étoile de déclinaison 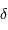 possède, du fait de la rotation diurne, une vitesse angulaire proportionnelle à
possède, du fait de la rotation diurne, une vitesse angulaire proportionnelle à 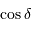 .
.
[2 points]
L'étoile traverse le champ de l'instrument, de diamètre angulaire 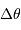 en une durée
en une durée 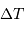 . Montrer que l'on a :
. Montrer que l'on a :
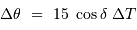
si le champ est mesuré en seconde d'arc et la durée en seconde de temps.
[2 points]
Vérifier la relation précédente avec les données de l'appliquette (pour tracer la fonction 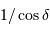 : sélectionner la 1ère ligne de la 3ème colonne (C1), et demander le calcul : = 1./15./cos(pi * B1 / 180.))
: sélectionner la 1ère ligne de la 3ème colonne (C1), et demander le calcul : = 1./15./cos(pi * B1 / 180.))
[1 points]
Avec les données de l'appliquette, déterminer dans les 2 cas (avec des grossissements différents) le diamètre angulaire du champ objet.
[1 points]
Les grossissements, dépendants de l'oculaire utilisé, valent respectivement 140 et 300. Montrer que les champs images ont une taille analogue au champ de vue de l'oeil humain, de l'ordre de 60 degrés.
[1 points]
pages_foyer-primaire/foyer-primaire-sexercer.html
pages_afocal/afocal-sexercer.html
pages_champ-ouverture/champ-ouverture-sexercer.html
pages_optiquegeo/champ-ouverture-sexercer.html
Application de la définition de l'ouverture d'un télescope.
Par définition, la focale 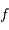 d'un télescope muni d'un miroir primaire de diamètre
d'un télescope muni d'un miroir primaire de diamètre 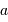 ouvert à
ouvert à 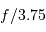 vaut :
vaut :
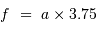
et donc 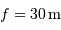
Faire un schéma de l'image au foyer d'un faisceau incliné d'un angle 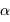 .
.
Un pixel voit un champ 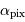 vérifiant :
vérifiant :
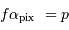
L'application numérique donne :
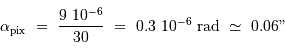
Le champ total, 2000 px, couvre une largeur de 120", soit 2'.
pages_optiquegeo/champ-ouverture-sexercer.html
Application directe de la définition de l'ouverture.
L'ouverture est f/15, car 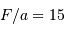 .
.
Si l'on parle d'oculaire, c'est pour observer à l'oeil, ceci conditionne le montage optique.
Le montage doit être afocal.
Le montage étant afocal, le grossissement est simplement :
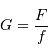
avec 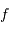 le focale de l'oculaire.
le focale de l'oculaire.
L'application numérique donne 200 et 300 respectivement, pour les oculaires de focale 45 et 30 mm.
Revoir l'expression du grossissement.
Dans le montage afocal, avec un angle du champ image 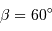 , l'angle du champ objet vérifie :
, l'angle du champ objet vérifie :
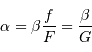
Les applications numériques donnent :
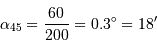
et
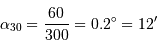
Ceci représente respectivement un peu plus ou un peu moins de la moitié du diamètre lunaire.