Les alignements d'objet, au-delà de leur côté parfois spectaculaires, apportent des mesures inédites, précieuses pour l'astrométrie.
Cette section traite ainsi des éclipses, occultations et transits, dans l'optique (réductrice) de faire le lien entre ces phénomènes et diverses mesures de distances, de longueur ou de position.

A partir du moment où les prédictions de transits et d'occultations furent possibles, elles ont motivé de lointains voyages, nécessaires pour rejoindre les régions où le phénomène est observable.
Crédit :
Bibliothèque de l'Observatoire de Paris
Bande de totalité
Une éclipse totale de soleil est un événement très ponctuel géographiquement et temporellement, donc exceptionnel.
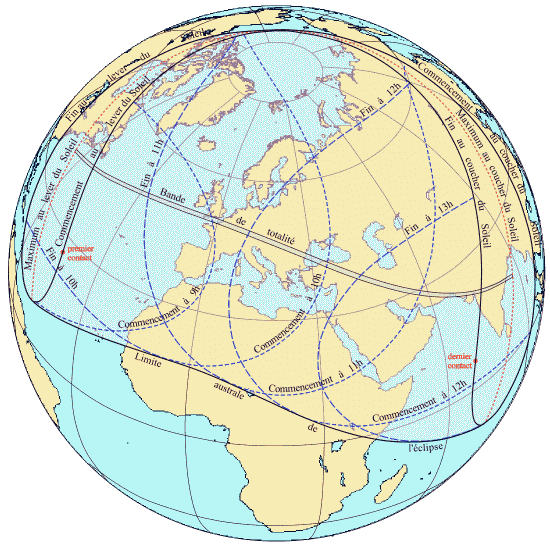
Conditions d'observation et bande de totalité de l'éclipse du 11 août 1999 (dernière éclipse totale visible en France)
Crédit :
IMCCE
Où et quand ?
La prédiction précise des éclipses est un exercice difficile, maîtrisé par un nombre restreint d'instituts dans le monde, qui relève de la métrologie du temps et de l'espace la plus poussée.
Voir les pages de l'IMCCE.
 Dis-moi comment tu tournes...
Dis-moi comment tu tournes...
Difficulté : ☆
Temps : 30
Question 1)
La durée de la rotation de la Terre est très proche de 86400 secondes (24 heures), mais sa valeur exacte est variable dans le temps. Le frottement provoqué par des effets de marées est à l'orgine d'un très lent ralentissement (de l'ordre de quelques millisecondes par siècle). Cela paraît peu, mais cumulé sur une période longue, il en resulte un décalage important.
Un des meilleurs moyens de mesurer cette variation consiste en l'étude d'observations historiques d'éclipses. Le décalage temporel (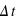 ) du moment précis d'une éclipse dû au ralentissement de la rotation de la Terre peut atteindre plusieurs heures! On trouve la relation mathématique suivante :
) du moment précis d'une éclipse dû au ralentissement de la rotation de la Terre peut atteindre plusieurs heures! On trouve la relation mathématique suivante :
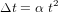 .
Ici,
.
Ici,  est la date de l'événement (compté en siècles avant 1820), et
est la date de l'événement (compté en siècles avant 1820), et  est mesuré en s par siecle2.
est mesuré en s par siecle2.
Un texte babylonien conservé au British Museum à Londres décrit une éclipse solaire totale, observée à Babylone le 15 avril de l'an 136 avant notre ère. En comparant l'heure de début et de fin décrits dans ce texte à un calcul des positions de la Terre et du Soleil, on trouve pour
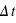 une valeur entre 11200 et 12150 secondes. Déduisez-en la valeur de la constante
une valeur entre 11200 et 12150 secondes. Déduisez-en la valeur de la constante 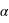 ainsi que son incertitude!
ainsi que son incertitude!
[
points]
136+1820-1 ans = 20 siècles
Question 2)
Un autre texte décrit une observation d'une éclipse totale, en Mésopotamie, il y a 40 siècles. A priori, l'observation état plus ancienne ( plus élevé), on pourrait espérer avoir une mesure plus précise de la valeur de
plus élevé), on pourrait espérer avoir une mesure plus précise de la valeur de 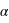 et du coup de mieux caractériser la rotation de la Terre.
et du coup de mieux caractériser la rotation de la Terre.
Le problème est que, dans ce cas, le texte ne mentionne pas le lieu d'observation. L'incertitude spatiale est de l'ordre de 1000 km le long de la bande de totalité, quasiment parallèle au parallèle de latitude 35 deg. Traduire l'incertitude spatiale en incertitude temporelle. Calculez aussi l'incertitude sur 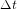 qui résulte de l'incertitude sur
qui résulte de l'incertitude sur  calculée à l'exercice précédent (1 s/siècle2).
calculée à l'exercice précédent (1 s/siècle2).
Calculer la longueur du parallèle 35 deg.
Question 3)
La date précise de l'éclipse est connue, par la mécanique céleste, plus précisement que la rotation de la Terre.
Cette éclipse permet-elle de préciser la rotation de la Terre ?
Occultation par un objet entouré d'une atmosphère
Lorsque qu'un objet du système solaire entouré d'une atmosphère occulte une étoile, la haute atmosphère joue le rôle de lentille.
La phase d'extinction présente des fluctuations d'intensité, reliées à la stratification des couches atmosphériques.

Crédit :
Observatoire de Paris/ASM
Observations multisites
L'observation de l'occultation sur plusieurs sites permet de déterminer les positions et longueurs des diverses cordes correspondant aux conditions locales d'observation de l'occultation. On en déduit la taille et la forme de l'objet occultant.
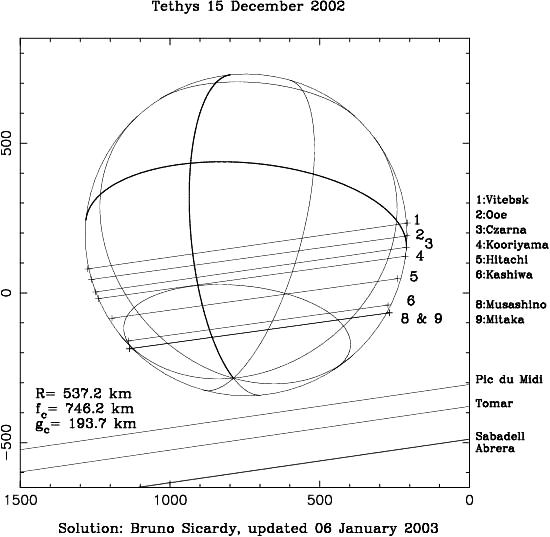
Reconstitution de la figure (=profil) de Tethys, satellite de Saturne, suite aux multiples observations de l'occultation du 15 décembre 2002.
Crédit :
Observatoire de Paris
 Objectifs
Objectifs
Montrer comment une occultation conduit, entre autres, à des mesures inaccessibles par ailleurs : taille et forme de l'objet occultant, sondage de son atmosphère...
Les occultations
Les occultations stellaires sont des phénomènes rares qui mettent en jeu
le passage d'une planète ou d'un satellite devant une étoile. Pendant
quelques minutes, il est alors possible de sonder avec une très grande
précision l'atmosphère du corps, s'il en possède une, de détecter ses
anneaux éventuels, ou de mesurer sa taille avec une précision kilométrique.
L'ombre et la pénombre
Une occultation, comme une éclipse, se caractérise par une ombre et une pénombre. La durée de l'ombre dépend essentiellement de la taille de l'objet du système solaire.
La durée de la pénombre dépend du diamètre stellaire (voir en exercice le principe de la mesure, et les échelles de temps associées). Il s'agit là d'une mesure très simple d'une grandeur par ailleurs inaccessible sans interférométrie.
Ombre et pénombre
La taille finie, non nulle, de l'étoile occultée implique une phase de pénombre, durant laquelle le disque stellaire disparaît ou réapparaît peu à peu.

Principe d'une occultation. La durée de la pénombre dépend du diamètre stellaire. La courbe de lumière de l'étoile (en bleu) mesure son flux en fonction du temps.
Crédit :
ASM
 Pénombre
Pénombre
Difficulté : ☆
Temps : 45 min
On cherche à estimer le diamètre angulaire d'une étoile occultée par un astéroïde.
On note 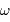 la vitesse angulaire de déplacement sur le ciel de l'objet du système solaire,
la vitesse angulaire de déplacement sur le ciel de l'objet du système solaire, 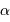 son diamètre angulaire,
son diamètre angulaire, 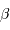 celui de l'étoile. On suppose l'occultation centrale (l'étoile, l'objet occultant et la Terre parfaitement alignés au centre de l'occultation).
celui de l'étoile. On suppose l'occultation centrale (l'étoile, l'objet occultant et la Terre parfaitement alignés au centre de l'occultation).
Question 1)
Dans une 1er temps, on fait l'hypothèse que le diamètre angulaire de l'étoile est négligeable. Déterminer la durée 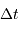 de l'occultation.
de l'occultation.
N'a-t-on pas 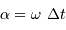 , par définition des variables ?
, par définition des variables ?
Question 2)
On ne suppose plus 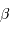 nul. Déterminer la durée des phases d'ombres et de pénombre. Déterminer les dates
nul. Déterminer la durée des phases d'ombres et de pénombre. Déterminer les dates 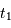 ...
... 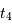 des premier contact, début puis fin de la totalité, dernier contact, en les repérant par rapport à la centralité.
des premier contact, début puis fin de la totalité, dernier contact, en les repérant par rapport à la centralité.
A quoi correspond la phase de pénombre ?
Quelle distance angulaire le satellite a-t-il parcouru durant l'occultation ?
Question 3)
Tracer l'allure de la courbe d'occultation.
Question 4)
A quelle condition peut-on mesurer les diamètres angulaire et linéaire de l'objet, de l'étoile ?
Déterminer les inconnues et les observables : vitesse angulaire, distances...
Question 5)
Les objets du système solaire ont typiquement une vitesse angulaire, notée en "/h, de 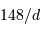 , avec
, avec 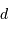 leur distance au soleil exprimée en UA.
La distance
leur distance au soleil exprimée en UA.
La distance 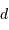 a été mesurée à 9.6 UA ; en déduire le rayon de l'objet pour un transit de durée moyenne (repérée par la mi-occultation) de T=12 s.
a été mesurée à 9.6 UA ; en déduire le rayon de l'objet pour un transit de durée moyenne (repérée par la mi-occultation) de T=12 s.
Il suffit de procéder dans l'ordre, et de calculer la vitesse angulaire, le rayon angulaire... ou de simplifier les calculs en prenant garde aux unités !
Question 6)
Chaque phase de pénombre a duré 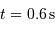 . En déduire le diamètre stellaire, l'étoile étant à
. En déduire le diamètre stellaire, l'étoile étant à 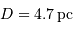 . Comparer le rayon stellaire calculé au rayon solaire.
. Comparer le rayon stellaire calculé au rayon solaire.
Obtenir d'abord le diamètre angulaire de l'étoile.
Pour passer du diamètre angulaire de l'étoile à son diamètre linéaire, appliquer directement la définition du parsec.
Un peu d'histoire
Les transits sont des phénomènes rares et localisés. Les observer a longtemps relevé du défi scientifique.
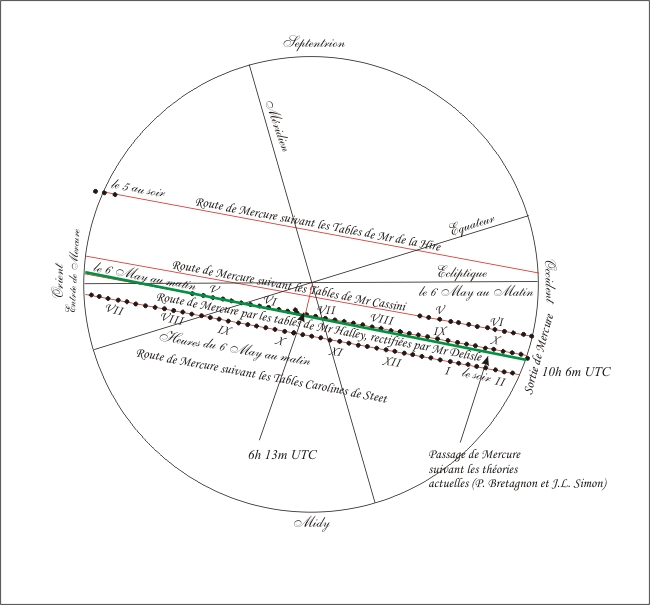
Transit de Mercure du 6 mai 1753 : diverses prédictions.
Crédit :
IMCCE
Transits de Mercure
Un transit apparaît simplement comme une ombre chinoise.

Aperçu du disque solaire, avec superposition de Mercure (à droite, proche du bord du Soleil), observé le 9 mai 2016 à Meudon. Remarquer l'assombrissement entre le centre et le bord du Soleil, puis la tâche solaire proche du centre du disque solaire.
Crédit :
Observatoire de Paris
La superposition de plusieurs clichés trace la trajectoire - une corde - du transit.

Le passage de Mercure devant le Soleil, en 1999, vu en lumière ultra-violette par le satellite Trace.
Crédit :
NASA
Les dernièrs transits de Mercure visible de la Terre ont eu lieu en mai 2016 et en novembre 2019. Les suivants auront lieu en 2032 et 2039.
Transits de Vénus
Vénus étant plus grande et plus proche de la Terre, son ombre apparaît bien plus importante sur le Soleil. L'inclinaison des orbites de Vénus et de la Terre conduit à un nombre très limité de transits. Les derniers transits de Venus ont eu lieu en 2004 et 2012. Pour les prochains, il faudra être patient : ce ne sera que en 2117 et 2125!

Aperçu du disque solaire, avec superposition de Vénus en ombre chinoise, et d'un avion qui passait par là, le 8 juin 2004.
Crédit :
Observatoire de Paris
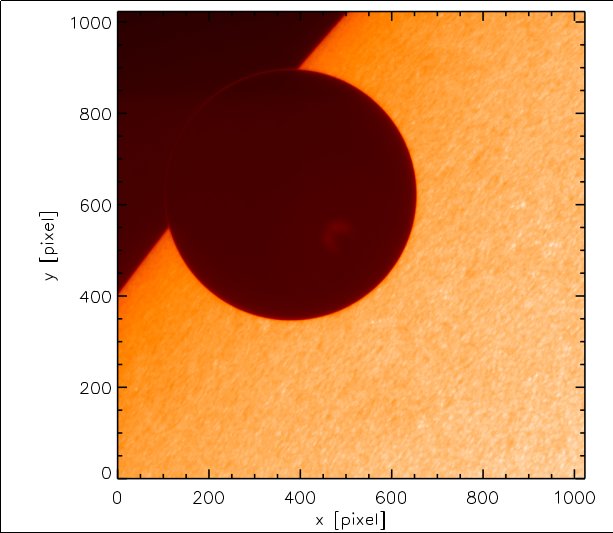
Passage de Venus devant le disque solaire le 5 juin 2012, observé par un spectro-polarimètre à bord du satellite Hinode.
L'auréole de Venus faiblement visible à gauche en haut (au bord de Venus, sur la partie qui ne se trouve pas devant le disque solaire)
est due à la lumière du Soleil refracté dans l'atmosphère de Venus.
Crédit :
Chiavassa et al., A&A 2015.
 Objectifs
Objectifs
On parle de transits lorsque Mercure ou Vénus passent devant le disque du soleil. Ces événements sont, comme les éclipses, rares mais instructifs.
Historiquement, les transits de Mercure et Vénus ont permis la mesure de l'unité astronomique.
Géométrie
La trace du disque planétaire sur le disque solaire est une simple projection. Il s'ensuit que différents observateurs verront des traces différentes, mais parallèles entre elles, évoluant à la même vitesse angulaire.
La différence entre les dates des premier et dernier contacts est proportionnelle à la longueur de la corde parcourue sur le disque.
La détermination de l'unité astronomique
Les transits ont permis la mesure de l'unité astronomique, comme l'a proposé l'astronome Halley. En effet, si la 3e loi de Kepler permet de figer le rapport entre les demi-grands axes de Vénus et de la Terre, elle ne permet pas d'en donner une mesure absolue.
Plutôt que de longs calculs, une animation montre le principe de la mesure.
Triangulation
Le point de vue de 2 observateurs différents permet de mettre en oeuvre le principe de mesure de distance par triangulation .

Transit : principe. Les échelles n'ont pas du tout été respectées (la Terre est un peu grande !)
Crédit :
ASM
La mesure de l'unité astronomique
La valeur de l'UA a pu être déterminée à partir de différentes observations d'un même transit. Les observables indépendantes sont :
- Le rapport des demi-grands axes planétaires (3e loi de Kepler)
- La dimension angulaire du soleil
L'écartement des cordes tracées par les ombres est d'autant plus grand que la distance terre-soleil est petite. La mesure de cet écartement (repéré par les dates des début et fin de transit à une époque où la photographie n'existait pas) permet de mesurer l'unité astronomique.
Lorsque la distance Terre-Soleil, inconnue a priori, notée A, croît :
- le diamètre angulaire du disque solaire étant fixé, le diamètre linéaire croît avec A.
- la distance relative de Vénus (ou Mercure) en unité A, fixée par la 3e loi de Kepler, croît également avec A, et la parallaxe planétaire décroît.
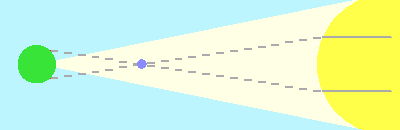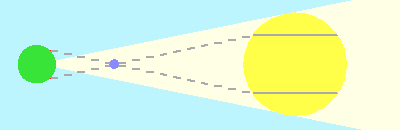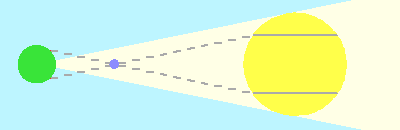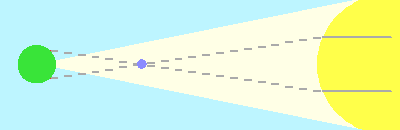
L'écartement entre les cordes est fonction de la distance Soleil-Terre. Cette dernière est ici variable, la distance relative du Soleil à Vénus étant elle fixée par la 3ème loi de Kepler. La mesure des cordes et leur comparaison permet donc la mesure de l'unité astronomique.
Crédit :
ASM
 Parallaxe
Parallaxe
Difficulté : ☆☆
Temps : 30
Question 1)
Déterminer la période de révolution synodique de Vénus. En déduire sa vitesse angulaire synodique autour du Soleil, puis sa vitesse linéaire synodique 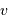 .
.
[3 points]
Question 2)
Quelle distance 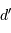 Vénus doit-elle parcourir sur son orbite pour un transit total le long du diamètre solaire
Vénus doit-elle parcourir sur son orbite pour un transit total le long du diamètre solaire 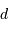 . En déduire la durée maximale d'un transit.
. En déduire la durée maximale d'un transit.
[2 points]
Question 3)
Estimer l'ordre de grandeur de la différence angulaire entre les traces de Vénus lors du transit du 8 juin 2004, pour 2 observateurs (l'un à Lille, l'autre à Perpignan, villes séparées de 1000 km).
[2 points]
Question 4)
Le transit dure 5h24min28s à Lille, et 5h24min58s à Perpignan.
Situer schématiquement l'allure des cordes correspondant au transit vues de Lille ou Perpignan : passent-elles proche d'un pôle (lequel ?) ou plutôt par l'équateur.
[2 points]
Au-delà de l'aspect événementiel, éclipses, occultations et transits sont des phénomènes scientifiques utiles et utilisés en astrophysiques. Ils permettent, comme on l'a vu, des mesures astrométriques extrêmement précises.
Ouverture sur ce sujet : l'observation et l'étude des phénomènes mutuels de Jupiter et Saturne, menées à l'IMCCE.
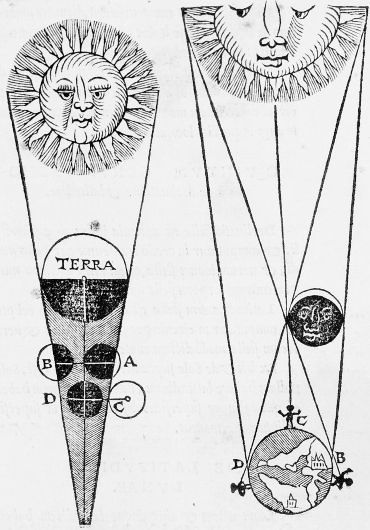
Jeux de Lune et Soleil. En quoi cette illustration reste-t-elle très moderne ?
Crédit :
Bibliothèque de l'Observatoire de Paris
- Question 1
Aide :
136+1820-1 ans = 20 siècles
Solution :
Pour 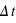 =11200 s, on trouve
=11200 s, on trouve  =28 s/siecle2.
Pour
=28 s/siecle2.
Pour 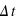 =12150 s, on trouve
=12150 s, on trouve  =30 s/siecle2.
Résultat:
=30 s/siecle2.
Résultat: 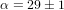 s/siecle2.
s/siecle2.
- Question 2
Aide :
Calculer la longueur du parallèle 35 deg.
Solution :
Incertitude de localisation : L'équateur mesurant 40 000 km, le parallèle à 35 deg mesure lui 32 700 km.
Une bande de longueur 1000 km est parcourue par la rotation de la Terre en
24 / 32.7 = 0.73 h, soit 44 min.
Incertitude de la rotation de la Terre : 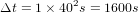 . Au bout de 40 siècles, l'incertitude est de l'ordre de 1600 s (un peu moins d'une demi-heure).
. Au bout de 40 siècles, l'incertitude est de l'ordre de 1600 s (un peu moins d'une demi-heure).
- Question 3
Solution :
La comparaison des 2 résultats précédents montre que
l'incertitude sur la localisation géographique, supérieure à l'incertitude temporelle sur la rotation de la Terre, ne permet pas de situer la Terre précisément par rapport à l'éclipse.
- Question 1
Aide :
N'a-t-on pas 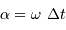 , par définition des variables ?
, par définition des variables ?
Solution :
La relation entre vitesse angulaire et angle conduit à
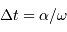 .
.
- Question 2
Aide :
A quoi correspond la phase de pénombre ?
Aide :
Quelle distance angulaire le satellite a-t-il parcouru durant l'occultation ?
Solution :
La phase de pénombre débute au 1er contact entre les 2 objets, jusqu'à ce que l'étoile soit totalement occultée. Cette phase de 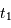 à
à 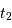 dure
dure 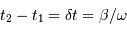 . Par symétrie,
. Par symétrie, 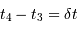 .
.
Lors de la phase de totalité, le satellite parcourt son diamètre moins celui de l'étoile. On a donc : 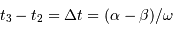 .
.
On en déduit, par rapport à la centralité 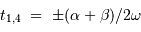 et
et 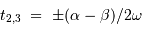 .
.
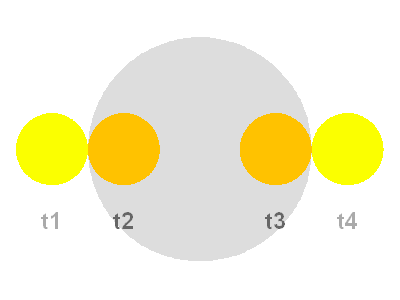
Crédit :
ASM
- Question 3
Solution :
Courbe de lumière de l'occultation. La flèche grise mesure la durée moyenne.
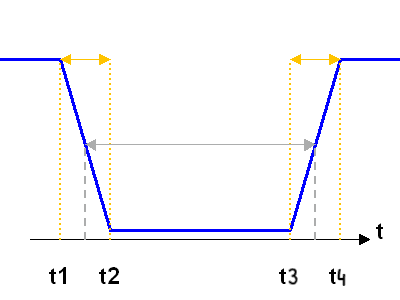
Crédit :
ASM
- Question 4
Aide :
Déterminer les inconnues et les observables : vitesse angulaire, distances...
Solution :
La vitesse angulaire 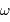 de l'objet est mesurable : les diamètres angulaires
de l'objet est mesurable : les diamètres angulaires 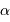 et
et 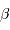 sont alors déterminés par les mesures de
sont alors déterminés par les mesures de 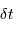 et
et 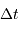 .
.
La distance au soleil de l'objet occultant peut être déduite, par application des lois de la gravitation, de son mouvement.
La mesure du diamètre linéaire de l'objet ou de l'étoile va dépendre de sa distance 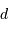 :
:
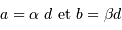
- Question 5
Aide :
Il suffit de procéder dans l'ordre, et de calculer la vitesse angulaire, le rayon angulaire... ou de simplifier les calculs en prenant garde aux unités !
Solution :
Avec une vitesse angulaire 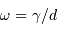 ,
, 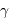 s'exprimant en UA."/h, le diamètre angulaire s'écrit
s'exprimant en UA."/h, le diamètre angulaire s'écrit
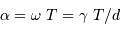 (AN : 0.05", en ayant pris soin d'exprimer le temps en heure, en accord avec l'unité de
(AN : 0.05", en ayant pris soin d'exprimer le temps en heure, en accord avec l'unité de 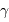 ).
).
Le diamètre linéaire 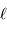 vérifie
vérifie 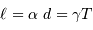 . L'application numérique donne
. L'application numérique donne 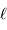 en UA."
en UA."
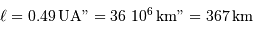 .
.
- Question 6
Aide :
Obtenir d'abord le diamètre angulaire de l'étoile.
Aide :
Pour passer du diamètre angulaire de l'étoile à son diamètre linéaire, appliquer directement la définition du parsec.
Solution :
Par règle de 3 entre les durées et les distances angulaires, le diamètre angulaire vaut :
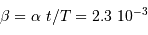 seconde d'arc.
seconde d'arc.
Passer du diamètre angulaire de l'étoile (donné en seconde d'arc) et de la distance (donnée en parsec) au diamètre linéaire de l'étoile par la définition du parsec donne le résultat simplement en UA.
A 4.7 pc, ce diamètre angulaire correspond à un diamètre linéaire 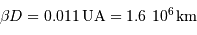 , très proche du diamètre du Soleil (1.4 millions de km).
, très proche du diamètre du Soleil (1.4 millions de km).
Remarquer que les durées à mesurer sont courtes.


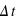 ) du moment précis d'une éclipse dû au ralentissement de la rotation de la Terre peut atteindre plusieurs heures! On trouve la relation mathématique suivante :
) du moment précis d'une éclipse dû au ralentissement de la rotation de la Terre peut atteindre plusieurs heures! On trouve la relation mathématique suivante :
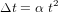 .
Ici,
.
Ici,  est la date de l'événement (compté en siècles avant 1820), et
est la date de l'événement (compté en siècles avant 1820), et  est mesuré en s par siecle2.
est mesuré en s par siecle2.
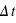 une valeur entre 11200 et 12150 secondes. Déduisez-en la valeur de la constante
une valeur entre 11200 et 12150 secondes. Déduisez-en la valeur de la constante 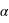 ainsi que son incertitude!
ainsi que son incertitude!
 plus élevé), on pourrait espérer avoir une mesure plus précise de la valeur de
plus élevé), on pourrait espérer avoir une mesure plus précise de la valeur de 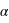 et du coup de mieux caractériser la rotation de la Terre.
et du coup de mieux caractériser la rotation de la Terre.
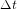 qui résulte de l'incertitude sur
qui résulte de l'incertitude sur  calculée à l'exercice précédent (1 s/siècle2).
calculée à l'exercice précédent (1 s/siècle2).



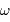 la vitesse angulaire de déplacement sur le ciel de l'objet du système solaire,
la vitesse angulaire de déplacement sur le ciel de l'objet du système solaire, 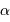 son diamètre angulaire,
son diamètre angulaire, 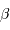 celui de l'étoile. On suppose l'occultation centrale (l'étoile, l'objet occultant et la Terre parfaitement alignés au centre de l'occultation).
celui de l'étoile. On suppose l'occultation centrale (l'étoile, l'objet occultant et la Terre parfaitement alignés au centre de l'occultation).
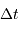 de l'occultation.
de l'occultation.
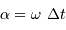 , par définition des variables ?
, par définition des variables ?
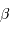 nul. Déterminer la durée des phases d'ombres et de pénombre. Déterminer les dates
nul. Déterminer la durée des phases d'ombres et de pénombre. Déterminer les dates 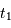 ...
... 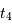 des premier contact, début puis fin de la totalité, dernier contact, en les repérant par rapport à la centralité.
des premier contact, début puis fin de la totalité, dernier contact, en les repérant par rapport à la centralité.
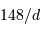 , avec
, avec 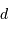 leur distance au soleil exprimée en UA.
La distance
leur distance au soleil exprimée en UA.
La distance 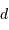 a été mesurée à 9.6 UA ; en déduire le rayon de l'objet pour un transit de durée moyenne (repérée par la mi-occultation) de T=12 s.
a été mesurée à 9.6 UA ; en déduire le rayon de l'objet pour un transit de durée moyenne (repérée par la mi-occultation) de T=12 s.
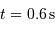 . En déduire le diamètre stellaire, l'étoile étant à
. En déduire le diamètre stellaire, l'étoile étant à 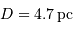 . Comparer le rayon stellaire calculé au rayon solaire.
. Comparer le rayon stellaire calculé au rayon solaire.







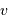 .
.
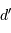 Vénus doit-elle parcourir sur son orbite pour un transit total le long du diamètre solaire
Vénus doit-elle parcourir sur son orbite pour un transit total le long du diamètre solaire 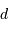 . En déduire la durée maximale d'un transit.
. En déduire la durée maximale d'un transit.

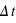 =11200 s, on trouve
=11200 s, on trouve  =28 s/siecle2.
Pour
=28 s/siecle2.
Pour 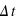 =12150 s, on trouve
=12150 s, on trouve  =30 s/siecle2.
Résultat:
=30 s/siecle2.
Résultat: 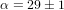 s/siecle2.
s/siecle2.
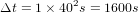 . Au bout de 40 siècles, l'incertitude est de l'ordre de 1600 s (un peu moins d'une demi-heure).
. Au bout de 40 siècles, l'incertitude est de l'ordre de 1600 s (un peu moins d'une demi-heure).
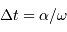 .
.
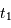 à
à 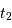 dure
dure 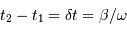 . Par symétrie,
. Par symétrie, 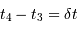 .
.
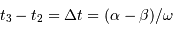 .
.
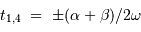 et
et 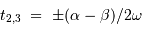 .
.


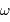 de l'objet est mesurable : les diamètres angulaires
de l'objet est mesurable : les diamètres angulaires 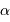 et
et 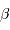 sont alors déterminés par les mesures de
sont alors déterminés par les mesures de 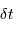 et
et 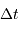 .
.
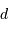 :
:
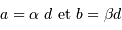
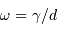 ,
, 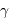 s'exprimant en UA."/h, le diamètre angulaire s'écrit
s'exprimant en UA."/h, le diamètre angulaire s'écrit
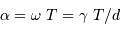 (AN : 0.05", en ayant pris soin d'exprimer le temps en heure, en accord avec l'unité de
(AN : 0.05", en ayant pris soin d'exprimer le temps en heure, en accord avec l'unité de 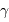 ).
).
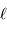 vérifie
vérifie 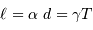 . L'application numérique donne
. L'application numérique donne 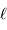 en UA."
en UA."
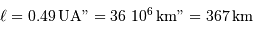 .
.
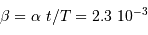 seconde d'arc.
seconde d'arc.
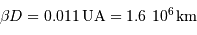 , très proche du diamètre du Soleil (1.4 millions de km).
, très proche du diamètre du Soleil (1.4 millions de km).