Les outils de modélisation et les équations à prendre en compte

Auteur: M. Turbet

Modèle 1D vs Modèle 3D, l'exemple

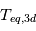Cas d'une planète en rotation synchrone, sans atmosphère, en tout point à l'équilibre thermique, et avec un albédo de surface constant A. On fait l'hypothèse très simpliste qu'une face reçoit en tout point un flux solaire constant alors qu'une autre ne reçoit pas du tout de flux. Pour ce cas particulier, on montre que $T_{eq,3d}$ ~ 0.59

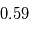
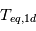$T_{eq,1d}$ .

Crédit : M. Turbet

Les processus physiques qui entrent en jeu dans l'évolution du climat d'une planète sont nombreux. En voici une liste non-exhaustive :

Equations de l'hydrodynamique (Navier Stokes) : Mouvement des parcelles d'air.
Equations de la thermodynamique : Condensation, Evaporation, Solidification des constituants de la planète.
Equations du transfert radiatif : Absorption, Emission, Réflection et Diffusion du flux solaire et du rayonnement thermique.
Equations de microphysique : Physique des nuages.
Equations chimiques : Photochimie.

La manière la plus réaliste de tenir compte de tous ces phénomènes physiques est d'utiliser un modèle de climat. Pour plus d'informations, veuillez vous reporter au cours sur les Modèles de Climat.

Modèle "Radiatif-Convectif" VS GCM

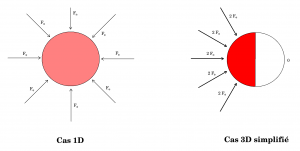
Dans un modèle Radiatif-Convectif, ou Modèle à 1 dimension, on représente la totalité de l'atmosphère d'une planète par une unique colonne composée d'un nombre discret de couches atmosphériques. Dans un GCM (Global Climate Model), ou Modèle à 3 dimensions, l'atmosphère est discrétisée selon les trois dimensions de l'espace.

Les modèles 3D ont l'avantage d'être plus complets et réalistes. Ils ont cependant le défaut d'être rapidement limités (par comparaison aux modèles 1D) par la puissance de calcul requis.

1D VS 3D : L'exemple de la température d'équilibre

Les modèles 1D comme celui-là ( accessible aussi là) sont plutôt fiables lorsqu'il s'agît de modéliser des planètes où la température de surface varie peu d'un point à un autre. C'est le cas des planètes avec une atmosphère très dense et/ou ayant une rotation suffisamment rapide. Dans le cas où il existe un contraste de température marqué entre deux points d'une même planète, le modèle 1D n'est plus représentatif de la planète. C'est notamment le cas des planètes en rotation synchrone, qui sont irradiées d'un côté (haute température) et pas de l'autre (basse température).

Prenons le cas d'une planète en rotation synchrone, sans atmosphère, en tout point à l'équilibre thermique, et avec un albédo de surface constant A. Et faisons l'hypothèse très simpliste qu'une face reçoit en tout point un flux solaire constant alors qu'une autre ne reçoit pas du tout de flux. Soit 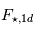$F_{\star,1d}$ le flux moyen reçu sur l'ensemble de la surface. Le bilan radiatif 1D donne : 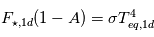$F_{\star,1d} (1-A) = \sigma T_{eq,1d}^4$ , soit 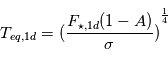$T_{eq,1d}= {(\frac{F_{\star,1d} (1-A)}{\sigma})}^{\frac{1}{4}}$ , avec 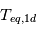$T_{eq,1d}$ la température moyenne d'équilibre de la planète (1D).

La planète est composée de deux faces d'aires égales : une éclairée et une autre non. Pour 50% de la planète, du côté de la face cachée, 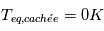$T_{eq,cach\'ee}=0 K$ . Pour les 50% restants, 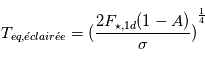$T_{eq,\'eclair\'ee}= {(\frac{2 F_{\star,1d} (1-A)}{\sigma})}^{\frac{1}{4}}$ car le côté éclairé de la planète reçoit un flux lumineux deux fois plus élevé que le flux moyen reçu sur l'ensemble de la surface, 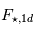$F_{\star,1d}$ . 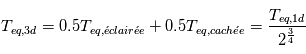La température moyenne d'équilibre de la planète (3D) vaut donc $T_{eq,3d}= 0.5 T_{eq,\'eclair\'ee} + 0.5 T_{eq,cach\'ee} = \frac{T_{eq,1d}}{2^{\frac{3}{4}}}$ .

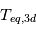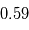
En bref, 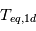$T_{eq,3d}$ ~ 0.59 $T_{eq,1d}$ ! Pour ce cas particulier, l'erreur est considérable. En fait, de manière plus générale, plus l'écart-type sur la température d'équilibre d'une planète est grand, plus l'erreur commise sur le calcul de sa température de surface par un modèle 1D sera grande.