
Etoiles de faible masse et synchronisation |
Plus une étoile a une faible masse, plus sa luminosité sera petite, et donc plus la Zone Habitable sera proche de cette étoile. Les Naines M, qui sont les étoiles les moins massives de la Séquence Principale (masse comprise entre 0,075 et 0,4 masse solaire) ont une Zone Habitable de 5 à 50 fois plus proche que celle autour du Soleil.
Plus une planète est proche de son étoile, plus les forces de marée exercées par son étoile sur elle vont s'accentuer.
Lorsqu'une planète orbite autour de son étoile, la force de gravité (qui diminue avec la distance) ressentie par la planète n'est pas la même en tout point. La partie de la planète la plus proche de son étoile est plus attirée par l'étoile que la partie lointaine. En conséquence, l'étoile déforme la planète et crée un renflement dans sa direction (et dans la direction opposée).
Si la planète tourne plus rapidement sur elle-même que sa révolution autour de son étoile, ce renflement va se décaler légèrement par rapport à l'axe Etoile-Planète. La planète étant un corps non-élastique, il faut en effet un laps de temps non-nul pour que le renflement revienne dans la direction de l'étoile.
En conséquence, il se crée un décalage angulaire 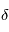 entre le renflement et la direction de l'étoile. Ceci a pour effet de créer un couple de rappel opposé au sens de rotation de la planète : la planète freine. Cet effet va durer tant que la vitesse de rotation de la planète est supérieure à sa vitesse de révolution. Dans cette situation, l'état d'équilibre le plus stable est la rotation synchrone.
entre le renflement et la direction de l'étoile. Ceci a pour effet de créer un couple de rappel opposé au sens de rotation de la planète : la planète freine. Cet effet va durer tant que la vitesse de rotation de la planète est supérieure à sa vitesse de révolution. Dans cette situation, l'état d'équilibre le plus stable est la rotation synchrone.
En fonction des propriétés de la planète et de son étoile, le temps qu'il faut pour qu'une planète se synchronise avec son étoile est très variable. On estime que 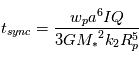 avec
avec 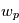 la vitesse de rotation initiale de la planète,
la vitesse de rotation initiale de la planète, 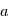 la distance Planète-Etoile,
la distance Planète-Etoile, 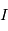 le moment d'inertie de la planète ( pour une sphère, on a par exemple
le moment d'inertie de la planète ( pour une sphère, on a par exemple 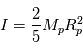 ),
), 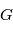 la constante gravitationnelle,
la constante gravitationnelle, 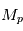 et
et 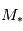 respectivement la masse de la planète et de l'étoile et
respectivement la masse de la planète et de l'étoile et 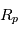 le rayon de la planète.
le rayon de la planète. 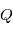 et
et 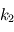 sont deux coefficients qui caractérisent la réponse de la planète aux forces de marée.
sont deux coefficients qui caractérisent la réponse de la planète aux forces de marée.
Finalement, on retiendra que 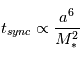 . On a
. On a 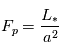 avec
avec 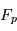 le flux reçu par la planète et
le flux reçu par la planète et 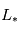 la luminosité de la planète. On choisit
la luminosité de la planète. On choisit 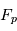 le flux moyen reçu par une planète habitable, indépendant de la planète et de l'étoile. Donc on a
le flux moyen reçu par une planète habitable, indépendant de la planète et de l'étoile. Donc on a 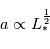 . Pour des étoiles de la Séquence Principale, on a de plus la relation Masse-Luminosité suivante :
. Pour des étoiles de la Séquence Principale, on a de plus la relation Masse-Luminosité suivante : 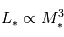 .
.
Bref, 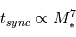 . Par exemple, en considérant ce mécanisme, une planète dans la Zone Habitable d'une Naine M de 0,2 masses solaires se synchronisera ~
. Par exemple, en considérant ce mécanisme, une planète dans la Zone Habitable d'une Naine M de 0,2 masses solaires se synchronisera ~ 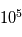 fois plus rapidement qu'une planète, comme la Terre, dans la Zone Habitable du Soleil.
fois plus rapidement qu'une planète, comme la Terre, dans la Zone Habitable du Soleil.
Note : Les forces de marée gravitationnelle peuvent être à l'origine de deux effets supplémentaires : 1. circulariser les orbites (les planètes en moyenne trop proches de leur étoile ont une excentricité qui diminue avec le temps) et 2. redresser l'obliquité (les planètes trop proches de leur étoile ont une obliquité qui tend vers 0).
En fait, lorsque la planête est entourée d'une atmosphère sufisamment épaisse, il existe une autre force de marée qui pourrait retarder voire empêcher la synchronisation d'une planète : la force de marée thermique.
Prenez une planète avec une atmosphère épaisse, comme Vénus par exemple. Lorsque le Soleil chauffe la zone subsolaire de cette planète, l'atmosphère s'y réchauffe et se dilate. La pression augmente en altitude. Pour équilibrer les forces de pression atmosphérique, une partie de la masse de l'atmosphère est redistribuée vers le coté nuit, créant cette fois-ci un renflement dans la direction perpendiculaire à la direction du Soleil.
Si la rotation d'une telle planète est plus rapide que sa révolution autour de son étoile , on aura un décalage angulaire 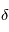 entre l'orientation du renflement et la perpendiculaire à la direction de l'étoile. Si
entre l'orientation du renflement et la perpendiculaire à la direction de l'étoile. Si 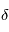 est inférieur à 180°, le renflement va provoquer un couple accélérateur du même sens que la rotation de la planète.
est inférieur à 180°, le renflement va provoquer un couple accélérateur du même sens que la rotation de la planète.
Si ce couple est suffisamment important, la période de rotation de la planète va converger vers un état d'équilibre différent de la rotation synchrone, où couples de marée gravitationnel et thermique se compensent. C'est par exemple ce qui est arrivé à Vénus.
Il y a finalement deux critères majeurs pour savoir si une planète habitable va finir en rotation synchrone ou non. Plus la masse de son étoile est faible, et moins son atmosphère est épaisse, plus les chances sont grandes pour que la planète entre (et rapidement) en rotation synchrone.