 Objectifs
Objectifs
Passer des coordonnées équatoriales, données par les catalogues, aux coordonnées azimutales, liées au lieu d'observation.
Hauteur d'un astre
En un lieu d'observation de latitude, 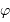 ,
les équations de passage des coordonnées équatoriales (ascension droite
,
les équations de passage des coordonnées équatoriales (ascension droite 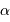 , déclinaison
, déclinaison 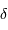 ) vers les coordonnées locales (azimut
) vers les coordonnées locales (azimut 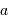 , hauteur
, hauteur 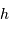 ) s'expriment par :
) s'expriment par :
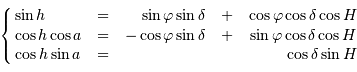
avec 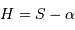 l'angle horaire,
l'angle horaire, 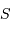 étant le temps sidéral.
étant le temps sidéral.
Conditions de visibilité
La visibilité d'un astre nécessite au moins 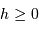 (astre au dessus de l'horizon), et en pratique
(astre au dessus de l'horizon), et en pratique 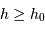 , la limite dépendant des contraintes d'observation.
, la limite dépendant des contraintes d'observation.
Les conditions posées sur l'angle horaire 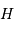 , et donc
, et donc 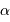 , sont estimées en exercice. Les équations précédentes montrent que le passage au méridien, l'altitude
, sont estimées en exercice. Les équations précédentes montrent que le passage au méridien, l'altitude 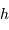 maximale, est atteint pour
maximale, est atteint pour 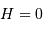 , càd
, càd 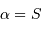 .
.
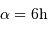 et déclinaison nulle à peu près toute la nuit (rappel :
et déclinaison nulle à peu près toute la nuit (rappel : 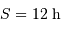 à l'équinoxe de printemps).
à l'équinoxe de printemps).
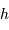 est positive, ce qui signifie :
est positive, ce qui signifie :
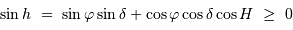
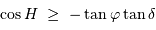
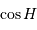 peut-il varier ?
peut-il varier ?
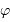 moyenne, un diagramme avec les étoiles circumpolaires (une étoile
moyenne, un diagramme avec les étoiles circumpolaires (une étoile 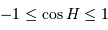 , l'inégalité précédente n'a pas de solution si
, l'inégalité précédente n'a pas de solution si 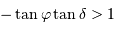 . Le cas limite est donc :
. Le cas limite est donc :
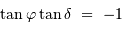
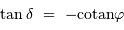
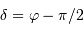 , et en tenant compte de l'inégalité, il n'y a aucune solution si
, et en tenant compte de l'inégalité, il n'y a aucune solution si
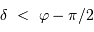
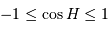 , l'inégalité précédente admet toujours une solution si
, l'inégalité précédente admet toujours une solution si 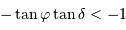 . Le cas limite est donc :
. Le cas limite est donc :
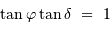
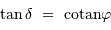
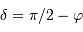 , et en tenant compte de l'inégalité, il y a toujours une solution si :
, et en tenant compte de l'inégalité, il y a toujours une solution si :
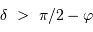
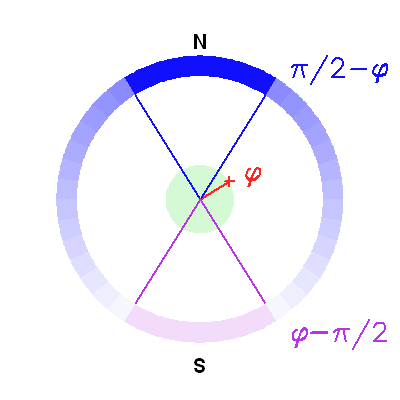
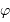 dans la région en violet.
dans la région en violet.