Introduction
Cette section est entièrement consacrée aux dates des saisons, elle aborde les notions d'année tropique, d'année sidérale et de calendriers solaires.
IntroductionCette section est entièrement consacrée aux dates des saisons, elle aborde les notions d'année tropique, d'année sidérale et de calendriers solaires.
La ligne des équinoxes n'est pas fixe. Elle est animée d'un mouvement de précession dans le sens rétrograde (50,288200" par an actuellement). Ce mouvement appelé précession des équinoxes est lié au mouvement de l'axe de rotation de la Terre qui décrit un cône dans le sens rétrograde en environ 26000 ans. L’année tropique moyenne ou révolution tropique est le temps que met la Terre pour faire une révolution autour du Soleil dans un repère tournant lié à la ligne des équinoxes, c’est donc la période liée à la différence entre la longitude moyenne du Soleil et la précession des équinoxes. Cette période est indépendante de l’origine choisie. Sa valeur moyenne pour l'époque J2000 est de 365,24219052 jours (soit 365 jours 5h 48m 45,26s). L'année tropique moyenne est différente du temps moyen que met la Terre pour aller d’un équinoxe de printemps à l’autre. En effet la vitesse de la Terre sur son orbite n’est pas uniforme, elle obéit, en première approximation, à la seconde loi de Kepler, donc le temps moyen mit pour aller d’un équinoxe de printemps à l’autre n’est pas égal au temps moyen qui sépare deux équinoxes d’automne et il en est de même pour les intervalles de temps séparant les solstices d’hiver et d’été. L'année tropique moyenne est est inférieure à l'année sidérale, qui correspond à l'intervalle de temps qui sépare deux passages de la Terre dans une même direction et qui est égale à 365,2563 jours (soit 365 jours 6h 9m 6s).
Cela est dû à notre calendrier, le calendrier grégorien, qui est construit de manière à avoir une longueur moyenne de l'année la plus proche possible de la révolution tropique de la Terre. Comme la révolution tropique n'a pas un nombre entier de jour, si on prend une année calendaire de 365 jours, il y a un décalage de 0,2422 jour d'une année à l'autre dans les dates des saisons et, au bout de quatre ans, ce décalage est presque de un jour. Pour compenser ce décalage on a, dans un premier temps, ajouté un jour à l'année tous les quatre ans (année bissextile de 366 jours). C'est ce que faisait le calendrier julien élaboré par Jules César en 46 avant J.-C. Mais si on ajoute un jour tous les quatre ans, la valeur moyenne de l'année calendaire est de 365,25 jours. Elle est donc un peu trop grande par rapport à l'année tropique. Donc si on se contente d'ajouter une année bissextile tous les quatre ans les saisons vont se décaler lentement par rapport au calendrier à raison de 0,0078 jour par an (11min 14s par an). Le calendrier julien suit donc mal les saisons. Il se décale d'environ 3 jours au bout de 400 ans. Pour avoir une meilleure concordance entre le calendrier et les saisons, il suffit de supprimer 3 jours sur une période de 400 ans.
C'est ce que l'on fait dans le calendrier grégorien. Comme dans le calendrier julien, on ajoute une année bissextile tous les quatre ans (ceux dont le millésime est multiple de quatre) sauf pour les années qui sont multiples de 100 sans l'être de 400. Ainsi 1600 et 2000 sont bissextiles, mais 1700, 1800, 1900 et 2100 ne sont pas bissextiles. Cette réforme du calendrier a été effectuée par le pape Grégoire XIII en 1582. De plus, pour supprimer le décalage accumulé entre les saisons et l'ancien calendrier (calendrier julien) et ramener la date de l'équinoxe de printemps au 21 mars, l'année 1582 a été raccourcie de 10 jours, le lendemain du jeudi 4 octobre 1582 devenant le vendredi 15 octobre 1582.
Année tropiqueNous avons vu que la période de révolution tropique moyenne de la Terre est de : 365,24219052 jours. Cette valeur est la combinaison du mouvement en longitude de la Terre dans un repère fixe et de la précession des équinoxes. La longitude moyenne de la Terre pour l'époque J2000 est donnée par la formule suivante :
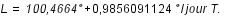
La précession des équinoxes en longitude dans le même repère est donnée par la formule :
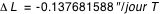
T est exprimé en jour. A partir de ces deux formules retrouver les périodes de révolutions sidérale et tropique de la Terre pour l'époque J2000.
Le programme de calcul des dates des saisons donne ces dates dans le calendrier julien pour les dates antérieures au 5 octobre 1582 et dans le calendrier grégorien pour les dates postérieures au 15 octobre 1582. Le calendrier julien a été prolongé pour les dates antérieures au début de l'ère chrétienne (calendrier proleptique). Dans l'affichage de ces dates on utilise la notation des astronomes et non pas la notation des historiens.
Comme nous l'avons vu dans un paragraphe précédent, les dates des saisons se décalent dans le calendrier julien d'environ 3 jours tous les 400 ans. On peut constater cette dérive à l'aide du programme de calcul des saisons.
| Année | Printemps | Eté | Automne | Hiver |
|---|---|---|---|---|
| 0 | 22 mars | 24 juin | 25 septembre | 22 décembre |
| -1000 | 30mars | 2 juillet | 2 octobre | 29 décembre |
| -2000 | 7 avril | 10 juillet | 9 octobre | 6 janvier |
| -3000 | 14 avril | 18 juillet | 15 octobre | 13 janvier |
| -4000 | 22 avril | 25 juillet | 22 octobre | 20 janvier |
Dérive de la date des saisons dans le calendrier julien
Nous l'avons vu, le calendrier grégorien est conçu pour éviter le décalage et la dérive des dates des saisons que nous avons constaté dans le calendrier julien. Les dates des saisons restent donc toujours au voisinage des mêmes dates dans le calendrier grégorien. L'utilisation des années bissextiles fait osciller l'instant des saisons sur trois et, exceptionnellement, quatre jours. Il ne faut pas confondre ces oscillations de la date des saisons autour de valeurs moyennes avec une dérive du calendrier.
Ces dates peuvent être vérifiées à l'aide du programme de calcul des saisons.
ConclusionLes dates des saisons sont fixes dans un calendrier, c'est-à-dire ne dérivent pas avec le temps, lorsque la durée moyenne de l'année calendaire est proche de la révolution tropique moyenne de la Terre. Ces calendriers portent le nom de calendrier solaire. Notre calendrier actuel, le calendrier grégorien est un calendrier solaire.