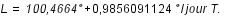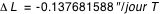Les saisons
Auteur: Patrick Rocher
- Introduction
- Définition des saisons astronomiques
- Introduction
- L'orbite de la Terre autour du Soleil
- La rotation de la Terre et l'équateur terrestre
- La ligne des équinoxes et la ligne des solstices
- Les équinoxes
- Exercice
- La durée des jours et des nuits
- Trajectoires apparentes du Soleil au début des différentes saisons
- Conclusion
- Les dates des saisons
- Introduction
- La révolution tropique
- Exercice
- Les dates des saisons dans les différents calendriers
- Les dates des quatre saisons
- Conclusion
- La durée des différentes saisons
- Introduction
- La longueur des saisons
- L'évolution de la longueur des saisons
- Conclusion
- Historique : saisons
- Introduction
- Historique: La précession des équinoxes et la longueur de l'année tropique
- Historique: La longueur des saisons
- Historique: Le nombre des saisons et le climat
- Historique: Trois saisons : en Égypte ancienne
- Historique: Quatre saisons décalées : en Chine
- Historique: Cinq saisons : en Australie
- Historique: Six saisons : en Inde
- Historique: Plus de six saisons
- Conclusion
- Conclusion
Introduction
 Prérequis
Prérequis
 Introduction
Introduction
Les climats terrestres dépendent de trois facteurs principaux : un facteur astronomique lié aux mouvements de la Terre autour du Soleil et à la rotation de la Terre sur elle-même; un facteur dynamique lié au déplacement saisonnier des masses d'air et un facteur thermique lié à la réflexion de la surface terrestre et au bilan radiatif. Nous traiterons principalement du premier facteur que l'on appelle les saisons astronomiques.
Nous allons définir les quatre saisons astronomiques qui sont en phase avec les hauteurs du Soleil et les durées du jour. Cela nous amènera à définir quelques termes parfois complexes mais qui permettent de mieux comprendre comment sont définies les dates et les durées des saisons. Nous comparerons enfin différents calendriers à différentes époques et en différents lieux sur Terre. Le facteur astronomique dominant est la hauteur du Soleil au-dessus de l'horizon. En effet plus le Soleil est haut, plus la quantité de chaleur reçue par mètre carré est importante, plus il fait chaud. La durée du jour n'est pas le phénomène prédominant, ainsi au pôle le jour dure plus de six mois mais il ne fait pas chaud car la hauteur du Soleil ne dépasse jamais 23°. Il n'y a donc pas de causalité entre la durée du jour et le climat, par contre la durée du jour peut intervenir dans les phénomènes météorologiques locaux (rosée, brises de mer). Les autres facteurs climatiques prennent souvent le pas sur l'échauffement dû à la hauteur du Soleil. Ainsi en France les journées les plus chaudes sont souvent celles du mois d'août alors que le Soleil est le plus haut dans le ciel au voisinage du solstice d'été (21 juin). La fraîcheur de mois de juin est due à un phénomène météorologique, une mini mousson produite par la présence de l'Atlantique.
Résumé
Les variations de hauteur du Soleil au cours du temps et les durées variables des jours sont dues à l'inclinaison de l'axe de rotation de la Terre sur l'orbite terrestre. Au cours de sa révolution autour du Soleil, la Terre passe par des positions particulières : les équinoxes et les solstices. Les dates et les longueurs des saisons ne sont pas toujours les mêmes mais on peut les calculer et les expliquer.
Définition des saisons astronomiques
Introduction
 Introduction
Introduction
Dans cette section nous allons décrire et définir le mouvement de la Terre autour du Soleil et sa rotation sur elle-même. Nous définirons ensuite la ligne des équinoxes et des solstices, puis nous étudierons les durées du jour et la trajectoire apparente du Soleil au début de chaque saison. Cette section donne de nombreuses définitions de termes astronomiques.
L'orbite de la Terre autour du Soleil
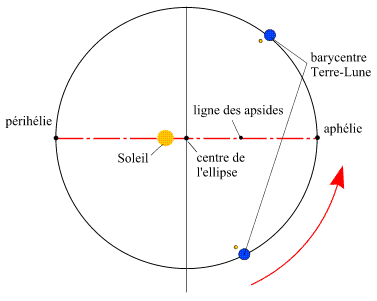
Orbite elliptique du barycentre Terre-Lune dans le plan de l'écliptique
Crédit : IMCCE/Patrick Rocher
En première approximation, le barycentre du système Terre-Lune parcourt, dans le sens direct (sens inverse des
aiguilles d'une montre), une orbite quasi elliptique et plane autour du Soleil (première loi de Kepler). Le plan de cette
orbite est appelé plan de l'écliptique. Le Soleil est situé à l'un des foyers de cette ellipse. L'excentricité de l'ellipse est tellement faible qu'elle est indécelable sur le tracé de l'orbite, le tracé ressemble à celui d'un cercle. Il est important de noter que le Soleil ne se trouve pas au centre de l'ellipse mais à l'un de ces foyers. La distance entre le barycentre Terre-Lune et le Soleil n'est donc pas constante. Il y a deux positions particulières correspondant aux valeurs extrêmes de cette distance : le périhélie (distance minimale) et l'aphélie (distance maximale). La ligne joignant ces deux positions s'appelle ligne des apsides.
La rotation de la Terre et l'équateur terrestre
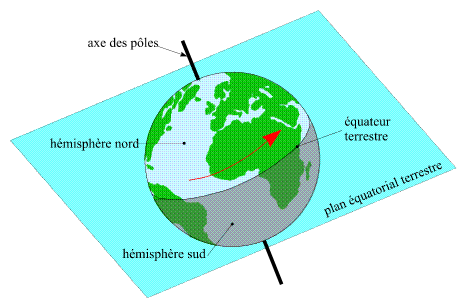
Rotation de la Terre : l'équateur terrestre
Crédit : IMCCE/Patrick Rocher
La Terre tourne sur elle-même, autour de l'axe des pôles, dans le sens direct (d'ouest en est). L'axe de rotation de la
Terre n'est pas normal au plan de l'orbite du barycentre Terre-Lune (plan de l'écliptique). Cette inclinaison, de 23° 26', est à l'origine des variations de la durée des jours et des nuits ainsi que des saisons. Le plan normal à l'axe de rotation
terrestre coupant en deux hémisphères la sphère terrestre s'appelle plan équatorial terrestre. L'intersection de ce plan
avec la Terre est l'équateur terrestre.
La ligne des équinoxes et la ligne des solstices
Comme l'axe de rotation de la Terre n'est pas normal au plan de l'écliptique, le plan équatorial terrestre n'est pas
parallèle au plan de l'écliptique. Il le coupe donc suivant une droite. Cette droite s'appelle la ligne des équinoxes.
Lorsque la direction du segment joignant le Soleil à la Terre est parallèle à celle ligne, la Terre se trouve aux équinoxes.
Il existe une autre ligne particulière, la ligne perpendiculaire, dans le plan de l'écliptique, à la ligne des équinoxes. Cette
ligne est la ligne des solstices. Lorsque la direction du segment joignant le Soleil à la Terre est parallèle à celle ligne, la Terre se trouve aux solstices.
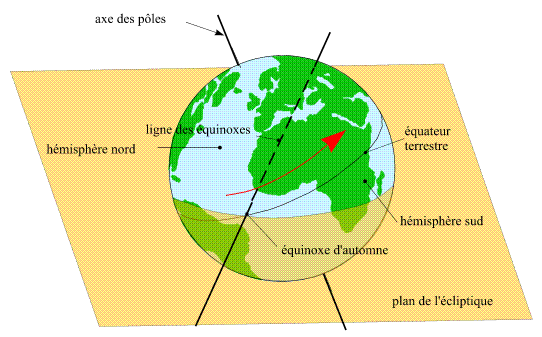
Ligne des équinoxes
Crédit : IMCCE/Patrick Rocher
Les équinoxes
Repère géocentrique équatorial
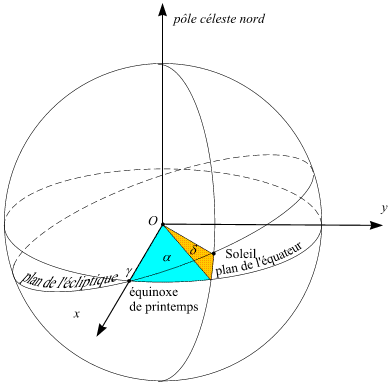
O : centre de la Terre, Oxy : plan de l'équateur, O
γ : direction de l'équinoxe de printemps, α : ascension droite, δ : déclinaison de l'astre
Crédit : IMCCE/Patrick Rocher
Vu de la Terre, dans le repère équatorial géocentrique, l'équinoxe correspondant au passage du Soleil des déclinaisons
négatives aux déclinaisons positives est appelé équinoxe de printemps (début du printemps dans l'hémisphère nord) ou
point vernal. Cette direction est, dans le plan de l'écliptique, l'origine des longitudes célestes et elle est également, dans
le plan de l'équateur, l'origine des ascensions droites.
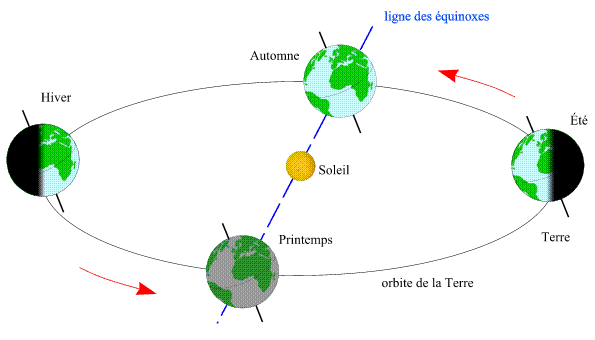
Saisons dans l'hémisphère nord
Crédit : IMCCE/Patrick Rocher
Le printemps, dans l'hémisphère nord, correspond donc à l'instant où la longitude géocentrique apparente du centre du Soleil est égale à 0°. L'autre équinoxe, correspondant au passage du Soleil des déclinaisons positives aux déclinaisons négatives, est appelé équinoxe d'automne (début de l'automne dans l'hémisphère nord). L'automne, dans l'hémisphère nord, correspond donc à l'instant où la longitude géocentrique apparente du centre du Soleil est égale à 180°.
Le solstice situé entre l'équinoxe de printemps et l'équinoxe d'automne est le solstice d'été et le solstice compris entre l'équinoxe d'automne et l'équinoxe de printemps est le solstice d'hiver. L'été, dans l'hémisphère nord, correspond donc à l'instant où la longitude géocentrique apparente du centre du Soleil est égale à 90°. De même, le solstice d'hiver, dans l'hémisphère nord, correspond à l'instant où la longitude géocentrique apparente du centre du Soleil est égale à 270°.
 Remarque
Remarque
Les saisons dans l'hémisphère sud sont inversées par rapport aux saisons dans l'hémisphère nord. Ainsi l'été dans l'hémisphère sud correspond à l'hiver dans l'hémisphère nord, l'hiver dans l'hémisphère sud correspond à l'été dans l'hémisphère nord, le printemps dans l'hémisphère sud correspond à l'automne dans l'hémisphère nord et l'automne dans l'hémisphère sud correspond au printemps dans l'hémisphère nord.
Exercice
 Saisons et équateur
Saisons et équateur
Question 1)
Nous venons de voir qu'il y a inversion des saisons entre l'hémisphère nord et l'hémisphère sud.
Pouvez-vous décrire en quelques lignes ce qui se passe lorsque l'on est à la limite des deux hémisphères, c'est-à-dire lorsque l'on est sur l'équateur ?
La durée des jours et des nuits
Le jour de l'équinoxe
Le jour de l'équinoxe (de printemps ou d'automne), si on néglige la réfraction atmosphérique, le terminateur de la zone de nuit sur la Terre passe par les deux pôles terrestres. Le jour de l'équinoxe, si on néglige la réfraction atmosphérique, la durée du jour est égale à la durée de la nuit pour tous les lieux de la surface terrestre. De plus, toujours en négligeant l'effet de la réfraction atmosphérique, le jour des équinoxes le Soleil se lève exactement à l'est et se couche exactement à l'ouest.
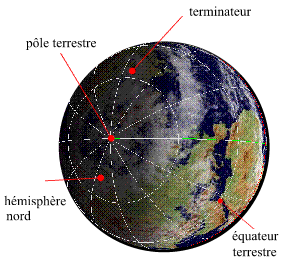
Le jour du solstice d'hiver
Le jour du solstice d'hiver, pour l'hémisphère nord, la demi-sphère définie par le terminateur de la zone de nuit
recouvre la plus grande partie de la surface de l'hémisphère nord. C'est le jour de l'année où la durée de la nuit est
maximale et la durée du jour minimale. C'est également le jour où le Soleil se lève le plus au sud-est (valeur extrême de l'amplitude ortive), passe au méridien avec une hauteur minimale et se couche le plus au sud-ouest(valeur extrême de l'amplitude occase).
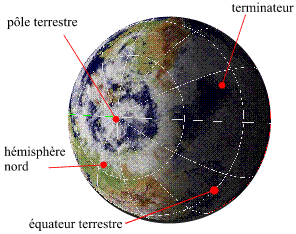
Le jour du solstice d'été
Le jour du solstice d'été, pour l'hémisphère nord, la demi-sphère définie par le terminateur de la zone de nuit recouvre
la plus petite partie de la surface de l'hémisphère nord. C'est le jour de l'année où la durée de la nuit est minimale et la
durée du jour maximale. C'est également le jour où le Soleil se lève le plus au nord-est (valeur extrême de l'amplitude ortive), passe au méridien avec une
hauteur maximale et se couche le plus au nord-ouest (valeur extrême de l'amplitude occase).
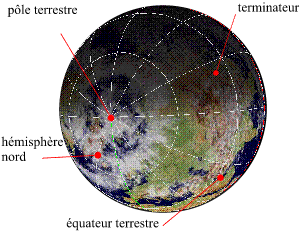
Equinoxes
Crédit : IMCCE/Patrick Rocher
Solstice d'hiver
Crédit : IMCCE/Patrick Rocher
Solstice d'été
Crédit : IMCCE/Patrick Rocher
Trajectoires apparentes du Soleil au début des différentes saisons
Nous rappelons que dans l'hémisphère sud, les solstices et les équinoxes sont à l'opposé des solstices et des équinoxes de l'hémisphère nord.
La Terre tourne autour de son axe dans le sens direct (d'ouest en est). Sur la Terre cela se traduit par un mouvement apparent des étoiles et des corps du système solaire dans le sens rétrograde (d'est en ouest).
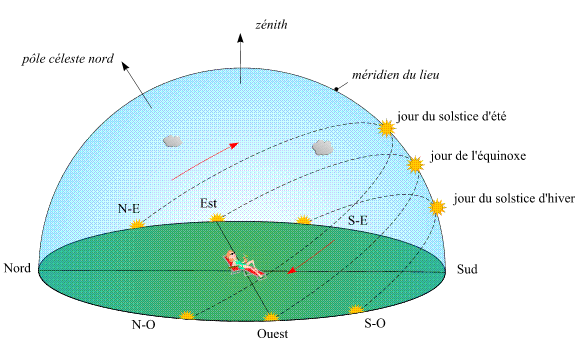
La figure illustre les trajectoires apparentes du Soleil pour chacune de ces journées en un lieu de l'hémisphère nord.
Crédit : IMCCE/Patrick Rocher
L'angle formé par la direction du lever du Soleil avec la direction de l'est porte le nom d'amplitude ortive, cette amplitude est nulle le jour des équinoxes et elle est maximale le jour des solstices.
De même l'angle formé par la direction du coucher du Soleil avec la direction de l'ouest s'appelle l'amplitude occase,
cette amplitude est nulle le jour des équinoxes et elle est maximale le jour des solstices.
 Conseils
Conseils
Il existe un moyen mnémotechnique pour se rappeler quelles amplitudes ortives ou occases correspond au coucher ou au lever d'un astre.
Les deux premières lettres des mots vous donnent la direction : OR pour ortive correspond à ORIENT donc à l'est donc au lever des astres (tous les astres se lèvent vers l'est), OC pour occase correspond à OCCIDENT donc à l'ouest donc au coucher des astres (tous les astres se couchent vers l'ouest).
Conclusion
 Conclusion
Conclusion
La Terre tourne autour du Soleil en suivant une orbite elliptique, sa vitesse sur cette orbite n'est pas constante. Les débuts des saisons astronomiques correspondent à quatre points particuliers de son orbite : les solstices et les équinoxes. Les valeurs extrêmes de la durée du jour et des positions du Soleil à son lever et à son coucher ainsi que sa hauteur correspondent aux jours des solstices.
Les dates des saisons
Introduction
 Introduction
Introduction
Cette section est entièrement consacrée aux dates des saisons, elle aborde les notions d'année tropique, d'année sidérale et de calendriers solaires.
La révolution tropique
La ligne des équinoxes n'est pas fixe. Elle est animée d'un mouvement de précession dans le sens rétrograde (50,288200" par an
actuellement). Ce mouvement appelé précession des équinoxes est lié au mouvement de l'axe de rotation de la Terre
qui décrit un cône dans le sens rétrograde en environ 26000 ans.
L’année tropique moyenne ou révolution tropique est le temps que met la Terre pour faire une révolution autour du Soleil dans un repère tournant lié à la ligne des équinoxes, c’est donc la période liée à la différence entre la longitude moyenne du Soleil et la précession des équinoxes. Cette période est indépendante de l’origine choisie. Sa valeur moyenne pour l'époque J2000 est de 365,24219052 jours (soit 365 jours 5h 48m 45,26s). L'année tropique moyenne est différente du temps moyen que met la Terre pour aller d’un équinoxe de printemps à l’autre. En effet la vitesse de la Terre sur son orbite n’est pas uniforme, elle obéit, en première approximation, à la seconde loi de Kepler, donc le temps moyen mit pour aller d’un équinoxe de printemps à l’autre n’est pas égal au temps moyen qui sépare deux équinoxes d’automne et il en est de même pour les intervalles de temps séparant les solstices d’hiver et d’été. L'année tropique moyenne est est inférieure à l'année sidérale, qui correspond à l'intervalle de temps qui sépare deux passages de la Terre dans une même direction et qui est égale à 365,2563 jours (soit 365 jours 6h 9m 6s).
Pourquoi les saisons tombent-elles toujours aux mêmes dates ?
Cela est dû à notre calendrier, le calendrier grégorien, qui est construit de manière à avoir une longueur moyenne de
l'année la plus proche possible de la révolution tropique de la Terre. Comme la révolution tropique n'a pas un nombre
entier de jour, si on prend une année calendaire de 365 jours, il y a un décalage de 0,2422 jour d'une année à l'autre
dans les dates des saisons et, au bout de quatre ans, ce décalage est presque de un jour. Pour compenser ce décalage on
a, dans un premier temps, ajouté un jour à l'année tous les quatre ans (année bissextile de 366 jours). C'est ce que
faisait le calendrier julien élaboré par Jules César en 46 avant J.-C. Mais si on ajoute un jour tous les quatre ans, la valeur moyenne de l'année calendaire est de 365,25 jours. Elle est donc un peu trop grande par rapport à l'année tropique. Donc si on se contente d'ajouter une année bissextile tous les quatre ans les saisons vont se décaler lentement par rapport au calendrier à raison de 0,0078 jour par an (11min 14s par an). Le calendrier julien suit donc mal les saisons. Il se décale d'environ 3 jours au bout de 400 ans. Pour avoir une meilleure concordance entre le calendrier et les saisons, il suffit de supprimer 3 jours sur une période de 400 ans.
C'est ce que l'on fait dans le calendrier grégorien. Comme dans le calendrier julien, on ajoute une année bissextile tous
les quatre ans (ceux dont le millésime est multiple de quatre) sauf pour les années qui sont multiples de 100 sans l'être de 400. Ainsi 1600 et 2000 sont bissextiles, mais 1700, 1800, 1900 et 2100 ne sont pas bissextiles. Cette réforme du calendrier a été effectuée par le pape Grégoire XIII en 1582. De plus, pour supprimer le décalage accumulé entre les saisons et l'ancien calendrier (calendrier julien) et ramener la date de l'équinoxe de printemps au 21 mars, l'année 1582 a été raccourcie de 10 jours, le lendemain du jeudi 4 octobre 1582 devenant le vendredi 15 octobre 1582.
Exercice
 Année tropique
Année tropique
Question 1)
Nous avons vu que la période de révolution tropique moyenne de la Terre est de : 365,24219052 jours.
Cette valeur est la combinaison du mouvement en longitude de la Terre dans un repère fixe et de la précession des équinoxes.
La longitude moyenne de la Terre pour l'époque J2000 est donnée par la formule suivante :
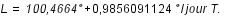
La précession des équinoxes en longitude dans le même repère est donnée par la formule :
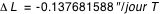
T est exprimé en jour.
A partir de ces deux formules retrouver les périodes de révolutions sidérale et tropique de la Terre pour l'époque J2000.
Les dates des saisons dans les différents calendriers
Le calcul des saisons à l'aide du programme
Le programme de calcul des dates des saisons donne ces dates dans le calendrier julien pour les dates antérieures au 5 octobre 1582 et dans le calendrier grégorien pour les dates postérieures au 15 octobre 1582. Le calendrier julien a été prolongé pour les dates antérieures au début de l'ère chrétienne (calendrier proleptique). Dans l'affichage de ces dates on utilise la notation des astronomes et non pas la notation des historiens.
La dérive des saisons dans le calendrier julien
Comme nous l'avons vu dans un paragraphe précédent, les dates des saisons se décalent dans le calendrier julien
d'environ 3 jours tous les 400 ans. On peut constater cette dérive à l'aide du programme de calcul des saisons.
| Année |
Printemps |
Eté |
Automne |
Hiver |
| 0 |
22 mars |
24 juin |
25 septembre |
22 décembre |
| -1000 |
30mars |
2 juillet |
2 octobre |
29 décembre |
| -2000 |
7 avril |
10 juillet |
9 octobre |
6 janvier |
| -3000 |
14 avril |
18 juillet |
15 octobre |
13 janvier |
| -4000 |
22 avril |
25 juillet |
22 octobre |
20 janvier |
Dérive de la date des saisons dans le calendrier julien
Les dates des saisons dans le calendrier grégorien
Nous l'avons vu, le calendrier grégorien est conçu pour éviter le décalage et la dérive des dates des saisons que nous avons
constaté dans le calendrier julien. Les dates des saisons restent donc toujours au voisinage des mêmes dates dans le
calendrier grégorien. L'utilisation des années bissextiles fait osciller l'instant des saisons sur trois et, exceptionnellement,
quatre jours. Il ne faut pas confondre ces oscillations de la date des saisons autour de valeurs moyennes avec une dérive du calendrier.
Les dates des quatre saisons
- Les dates de l'équinoxe de printemps : Aux XIXe et XXe siècles, l'équinoxe de printemps tombe toujours le 20 ou le 21 mars. Dans le passé il est tombé
le 19 mars en 1652, 1656, 1660, 1664, 1668, 1672, 1676, 1680, 1684, 1685, 1688, 1689, 1692, 1693, 1696,
1697, 1780, 1784, 1788, 1792 et 1796.
Il tombera de nouveau le 19 mars en 2044.
- Les dates du solstice d'été : Dans le calendrier grégorien, le solstice d'été peut tomber les 19, 20, 21 ou 22 juin. En général, il tombe le 21 juin. Il
est tombé un 20 juin en 1896 et tombera de nouveau à cette date en 2008. Il est tombé un 22 juin en 1975 et tombera
de nouveau à cette date en 2203, 2207, 2211 et 2215 puis en 2302. Le solstice d'été tombera un 19 juin en 2488 (et
ce sera la première fois depuis la création du calendrier grégorien) puis en 2492 et 2496.
- Les dates de l'équinoxe d'automne : Dans le calendrier grégorien, l'équinoxe d'automne peut tomber le 21, 22, 23 ou 24 septembre. Il tombe en général le
22 ou le 23 septembre. Il tombera le 21 septembre en 2092 et ce sera la première fois depuis la création du calendrier
grégorien. Cela se reproduira en 2096, puis en 2464, 2468, 2472, 2476, 2480, 2484, 2488, 2492, 2493, 2496 et
2497. Il est tombé un 24 septembre en 1803, 1807, 1903, 1907, 1911, 1915, 1919, 1923, 1927 et 1931, il tombera
de nouveau à cette date en 2303.
- Les dates du solstice d'hiver : Dans le calendrier grégorien le solstice d'hiver peut tomber le 20, 21,22 ou 23 décembre. Il tombe en général le 21 ou
le 22 décembre. Il est tombé un 23 décembre en 1903 et tombera de nouveau à cette date en 2303, 2307, 2311 et
2315. Il est tombé un 20 décembre en 1664, 1668, 1672, 1676, 1680, 1684, 1688, 1692, 1696 et 1697 et tombera
de nouveau à cette date en 2080, 2084, 2088, 2092, 2096, 2488, 2492 et 2496.
Ces dates peuvent être vérifiées à l'aide du programme de calcul des saisons.
Conclusion
 Conclusion
Conclusion
Les dates des saisons sont fixes dans un calendrier, c'est-à-dire ne dérivent pas avec le temps, lorsque la durée moyenne de l'année calendaire est proche de la révolution tropique moyenne de la Terre. Ces calendriers portent le nom de calendrier solaire. Notre calendrier actuel, le calendrier grégorien est un calendrier solaire.
La durée des différentes saisons
Introduction
 Introduction
Introduction
Cette section traite de la longueur des saisons et de l'évolution de la longueur des saisons en fonction du temps.
La longueur des saisons
Il suffit de consulter un calendrier pour vérifier que les longueurs des différentes saisons ne sont pas égales. Par exemple durant l'année 1998, l'hiver a duré 89 jours, le printemps 92 jours 18 heures, l'été 93 jours 15 heures et l'automne 89 jours 21 heures.
Cette variation des longueurs des saisons provient du fait que la vitesse du barycentre Terre-Lune sur son orbite autour du Soleil n'est pas un mouvement uniforme. C'est une conséquence immédiate de la seconde loi de Kepler. La vitesse orbitale n'est pas constante. Lorsque le barycentre Terre-Lune est au plus près du Soleil (à son périhélie) sa vitesse est maximale et lorsque le barycentre Terre-Lune est au plus loin du Soleil (à son aphélie) sa vitesse est minimale. Or actuellement le barycentre Terre-Lune passe au périhélie début janvier et à l'aphélie début juillet. Donc la Terre est plus rapide sur son orbite en janvier et l'hiver est la saison la plus courte, de même elle est la plus lente en juillet et l'été est la saison la plus longue.
Durée des saisons
| Année |
Durée de l'hiver |
Durée du printemps |
Durée de l'été |
Durée de l'automne |
Date du passage au périhélie |
Date du passage à l'aphélie |
| 130 avant J. -C. |
90 jours 5h 39m 58s |
94 jours 0h 21m 33s |
92 jours 8h 24m 42s |
88 jours 15h 25m 7s |
1 décembre à 5h 43m 23s |
2 juin à 21h 11m 54s |
| 2004 |
88 jours 23h 44m 49s |
92 jours 18h 8m 14s |
93 jours 15h 32m 57s |
89 jours 20h 11m 46s |
4 janvier à 17h 41m 59s |
5 juillet à 10h 53m 28s |
Comparaison de la durée des saisons entre l'an 130 avant J.-C. et l'an 2004.
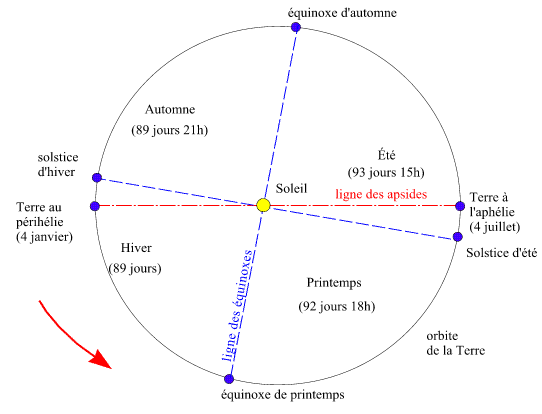
Durée des saisons pour l'année 1998
Crédit : IMCCE/Patrick Rocher
Cette figure montre bien que la saison n'est pas fonction de la distance entre le Soleil et la Terre. Actuellement, dans l'hémisphère nord, la saison la plus froide (l'hiver) correspond à l'époque où le Soleil est le plus près de la Terre et la saison la plus chaude (l'été) correspond à l'époque où le Soleil est le plus loin de la Terre.
L'évolution de la longueur des saisons
Si les positions du périhélie et de l'aphélie du barycentre Terre-Lune étaient constantes dans le temps, la durée des différentes saisons serait, elle aussi, constante. Mais l'orbite du barycentre Terre-Lune tourne dans son plan dans le sens direct à raison d'environ 12" par an (soit une révolution en environ 100 000 ans), ce mouvement est donc un mouvement direct de la ligne des apsides. La précession des équinoxes
s'effectue dans le sens contraire (sens rétrograde) à raison de 50,288200" par année julienne de 365,25 jours (soit une révolution en environ 26000 ans). La combinaison de ces deux mouvements permet de calculer la période du passage du périhélie de la Terre par la direction de l'équinoxe de printemps, cette période d'environ 21 000 ans est appelée précession climatique. En effet, tous les 10500 ans (demi-période de la précession climatique) l'aphélie passe de l'été à l'hiver. Or même si la distance Terre-Soleil n'est pas le facteur prédominant dans la nature des saisons, la combinaison du passage de la Terre à l'aphélie en hiver donne des hivers plus rudes. De même la distance Terre-Soleil dépend également de la variation de l'excentricité de l'orbite terrestre. Ainsi les périodes glacières sont corrélées avec les minima de l'excentricité de l'orbite terrestre.

Mouvement de l'équinoxe et de l'axe des apsides
Crédit : IMCCE/Patrick Rocher
Conclusion
 Conclusion
Conclusion
L'inégalité de la longueur des saisons est due à la non uniformité du mouvement orbital de la Terre autour du Soleil. La variation des longueurs des saisons est due au mouvement de la ligne des apsides de la Terre.
Historique : saisons
Introduction
 Introduction
Introduction
Cette section traite des aspects historiques et géographiques des saisons. Très tôt les astronomes ont essayé de construire des calendriers solaires, pour cela ils durent mesurer et estimer la durée de l'année tropique. En fonction des lieux géographiques, les autres facteurs climatiques jouent des rôles plus ou moins prononcés, ainsi le nombre des saisons climatiques n'est pas toujours égal aux quatre saisons astronomiques.
Historique: La précession des équinoxes et la longueur de l'année tropique
Le nom d'Hipparque de Nicée (env. 190 - env. 125 av. J.-C.) est lié à la découverte de la précession des équinoxes.
Pour découvrir ce lent mouvement de la ligne des équinoxes, deux méthodes d'observations sont possibles. La
première consiste à mesurer les variations des longitudes des étoiles au cours du temps. Cette méthode est cumulative, car chaque année la longitude croit d'une valeur faible mais constante. La deuxième méthode consiste à mesurer l'écart entre l'année tropique et l'année sidérale. Nous savons grâce à Ptolémée (IIe siècle après J.-C.) qu'Hipparque a utilisé ces deux méthodes. Et c'est vraisemblablement la première qui fut à l'origine de sa découverte de la précession des équinoxes. Pour cela il compara la distance de Spica dans l'Épi de la Vierge (l'étoile alpha Virginis) avec l'équinoxe d'automne aux dates des observations de Timocharis, observations faites entre 294 et 283 av. J.-C. et la valeur de cette même distance à son époque, et il trouva une variation dans la longitude de l'étoile de 2° sur la période de 160 ans séparant les deux mesures.
Pour la détermination des valeurs de l'année tropique et de l'année sidérale, Hipparque utilisa dans un premier temps des observations faites entre 162 et 128 av. J.-C., mais les valeurs calculées à partir de ces observations semblaient indiquer une valeur variable de l'année tropique en fonction du temps. Finalement, il se limita aux observations des solstices qu'il avait effectuées lui-même en 135 av. J.-C., aux observations faites par Aristarque en 280 av. J.-C. et aux observations faites par Méton, en 432 av. J.-C. Pour l'année tropique il trouva une valeur de 365 jours 1/4 moins 1/300 jour (soit 365 jours 5h 55m 12s) et pour l'année sidérale, il trouva une valeur de 365 jours 1/4 plus 1/144 jour (soit 365 jours 6h 10m 0s). Ces valeurs sont assez proches des valeurs actuelles.
En réalité la valeur de l'année tropique n'est pas constante, mais varie lentement en fonction du temps, sa valeur est donnée pour un instant donné par la relation suivante (P. Bretagnon, 2000) :
A =365,242 190 516 6 - 61,560 7 x 10 -6 T - 68,4 x 10 -9 T 2 + 263,0 x 10 -9 T 3+ 3,2 x 10 -9 T 4
où T = (JJD - 2 451 545,0) / 365 250
JJD étant le jour julien de l'époque considérée.
valeurs de l'année tropique
| Epoque |
Auteur |
Valeur |
| 141-127 av. J.-C. |
Hipparque |
365j 5h 55m 12s |
| 45 av. J.-C. |
Jules César (Sosigène) |
365j 5h 55m |
| 139 ap J.-C. |
Ptolémée |
365j 5h 55m 12s |
| 499 |
Aryabhata |
365j 8h 36m 30s |
| 882 |
al-Battani |
365j 5h 48m 24s |
| ~1100 |
Khayam |
365j 5h 49m 12s |
| 1252 |
Tables Alphonsines |
365j 5h 49m 16s |
| ~1440 |
Ulug Beg |
365j 5h 49m 15s |
| 1543 |
Copernic |
365j 5h 49m 29s |
| 1574-1575 |
Danti |
365j 5h 48m |
| 1582 |
Calendrier Grégorien |
365j 5h 48m 20s |
| 2000 |
Bretagnon |
365j 5h 48m 45.26s |
Le tableau suivant donne les différentes valeurs de l'année tropique en fonction de l'époque.
Historique: La longueur des saisons
Le Papyrus d'Eudoxe, nous informe que Callipe (vers 370-330 av. J.-C.) fut un des premiers astronomes à déterminer avec précision la longueur des différentes saisons. Il trouva (94, 92, 89 et 90 jours) à partir de l'équinoxe de printemps.
Hipparque améliora ces valeurs et trouva (94 1/2, 92 1/2, 88 1/8 et 90 1/8) toujours à partir de l'équinoxe de
printemps. On remarquera que ces valeurs sont très différentes des valeurs actuelles et cela est normal. En effet, si l'on tient compte de la précession climatique, l'angle entre le périhélie et l'équinoxe de printemps était à l'époque d'Hipparque 34° plus grand qu'actuellement. Le périhélie tombait donc en automne et l'aphélie au printemps, et la saison la plus courte était effectivement l'automne et la saison la plus longue, le printemps.
Historique: Le nombre des saisons et le climat
Les variations de la hauteur du Soleil dans la journée est un des éléments moteurs du climat, ainsi plus on monte en latitude vers les pôles plus le Soleil reste bas sur l'horizon et plus on s'approche de l'équateur plus le Soleil monte haut dans le ciel. D'autres éléments -- la présence des mers et des océans, la présence de la végétation, la nature du relief -- interviennent localement et produisent les différents types de climats observables sur Terre. Ainsi si sous nos latitudes les quatre saisons sont relativement en phase avec les variations climatiques, dans d'autres régions les quatre saisons sont moins marquées et historiquement, leurs nombres et leurs durées sont différentes.
Deux saisons : en Mésopotamie, au Soudan
En Mésopotamie, l'année solaire est divisée en deux saisons de six mois chacune : l'été ou temps de chaleur, (en
sumérien Emesh, en akkadien ummatum) commence à l'équinoxe de printemps, et l'hiver ou temps du froid (en
sumérien Enten, en akkadien kussu) commence à l'éqinoxe d'automne. C'est plutôt le régime des pluies débutant vers le mois de septembre et la crue du Tigre et de l'Euphrate croissante de novembre à mars et maximale en avril et mai, éléments déterminant pour les travaux agricoles, qui sont à l'origine de ce découpage en deux saisons.
On retrouve une pratique identique de nos jours, chez les Nuer du Haut Nil (au Soudan) où l'année est divisée en deux saisons. Une saison des pluies de mars à septembre durant laquelle les Nuer mènent une vie sédentaire et une saison de sècheresse d'octobre à février où les Nuer reprennent une vie nomade.
Historique: Trois saisons : en Égypte ancienne
Dans l'Égypte ancienne, le nombre de saisons était de trois, chaque saison comportait quatre mois. Les noms des
saisons et des mois sont donnés dans le tableau suivant :
Saisons Égypte
| Saison |
Nom des mois |
| Inondation (Aklet) |
Thot-Paophi-Athyr-Choeac |
| Hiver (Peret) |
Tybi-Méchir-Phaminoth-Pharmouti |
| Été (Shemou) |
Pachon-Payni-Epiphi-Mésori |
L'année commence avec la saison de l'inondation et cela correspond au début de la crue du Nil. On lit souvent que la crue du Nil correspondait avec le lever héliaque de l'étoile Sirius (Sothis chez les égyptiens), et que le lever héliaque de Sirius a lieu le jour du solstice d'été. En réalité la crue du Nil est bien évidement liée à un phénomène saisonnier et ce phénomène a du, à une époque donnée, correspondre au lever héliaque de Sirius, mais le lever héliaque de Sirius ne se produit pas à date fixe, sa date varie avec la précession des équinoxes et dépend également de la latitude du lieu d'observation.
Historique: Quatre saisons décalées : en Chine
En Chine, l'année tropique est divisée en 24 sections de saisons - les Jié Qì - correspondant chacune à un arc de 15 degrés de longitude, on distingue quatre saisons comme sous nos latitudes, mais elles sont décalées par rapport aux nôtres d'un mois et demi. Ainsi contrairement aux conventions occidentales, les saisons débutent lorsque la longitudes du Soleil atteint 315°, 45°, 135° et 225° (pour le printemps, l'été, l'automne et l'hiver) et non pas aux équinoxes et aux solstices. Le printemps commence donc à mi-chemin entre le solstice d'hiver et l'équinoxe de printemps.
Dans les Jiè Qì les termes principaux Z sont appelés zhong qì.
Liste des Jié Qì
| Numéro |
Jié Qi |
Nom |
Longitude du Soleil |
| J1 |
Lì chun |
début du printemps |
315° |
| Z1 |
Yu shui |
pluies |
330° |
| J2 |
Jing zhé |
réveil des insectes |
345° |
| Z2 |
Chun fen |
équinoxe de printemps |
360° |
| J3 |
Qinq ming |
clarté |
15° |
| Z3 |
Gu yu |
pluies des grains |
30° |
| J4 |
Lì xià |
début de l'été |
45° |
| Z4 |
Xiao man |
petite abondance |
60° |
| J5 |
Máng zhong |
grains en épi |
75° |
| Z5 |
Xià zhì |
solstice d'été |
90° |
| J6 |
Xiao shu |
petite chaleurs |
105° |
| Z6 |
Dà shu |
grandes chaleurs |
120° |
| J7 |
Lì qiu |
début de l'automne |
135° |
| Z7 |
Chu shu |
fin des chaleurs |
150° |
| J8 |
Bái lù |
rosée blanche |
165° |
| Z8 |
Qiu fen |
équinoxe d'automne |
180° |
| J9 |
Hán lù |
rosée froide |
195° |
| Z9 |
Shuang Jiáng |
arrivée du givre |
210° |
| J10 |
Lì dong |
début de l'hiver |
225° |
| Z10 |
Xiao xue |
petites neiges |
240° |
| J11 |
Dà xue |
grandes neiges |
255° |
| Z11 |
Dong zhì |
solstice d'hiver |
270° |
| J12 |
Xiao hán |
petits froids |
285° |
| Z12 |
Dà hán |
grands froids |
300° |
Le tableau donne la liste des Jié Qì.
Historique: Cinq saisons : en Australie
Les aborigènes de la région de Kakadu (Australie) découpent l'année solaire en cinq saisons. En Gundjeidmi, la langue des Maiili, les saisons portent les noms suivants :
Saisons Kakadu
| Nom des saisons |
Traduction |
| yegge |
saison plus fraîche, mais encore humide |
| wurrgeng |
saison froide |
| gurrung |
saison chaude et sèche |
| gunumeleng |
saison des tempêtes d'avant la mousson |
| banggereng |
saison des tempêtes renverse tout |
Historique: Six saisons : en Inde
En Inde le nombre des saisons est de six, chaque saison ayant deux mois.
Le tableau suivant donne la liste des saisons ainsi que les mois du calendrier solaire indien correspondant à ces saisons avant la réforme calendaire de 1957.
Saisons Inde
| Saison |
Nom des mois dans le calendrier solaire |
| Hiver (Sisira) |
Pausa - Magha |
| Printemps (Vasanta) |
Phalguna - Chaitra |
| Été (Grisma) |
Vaisakha - Jyaistha |
| Pluies (Varsa) |
Asadha - Sravana |
| Automne (Sarat) |
Bhadra - Asvina |
| Froid (Hermana) |
Kartika - Agrahayana |
Les mois en Inde
La réforme du calendrier de 1957 a imposé un calendrier solaire identique au calendrier grégorien commençant le 1 Chaitra (22 mars). Dans ce nouveau calendrier, suite à la précession des équinoxes, les dates des saisons ont été décalées d'un mois pour compenser cet écart (qui est en réalité de six semaines).
Historique: Plus de six saisons
Assez paradoxalement, c'est au nord du cercle polaire que l'on trouve une division de l'année comportant plus de six saisons. Les Inuit utilisaient un calendrier lunaire, qui était en réalité plus lié aux variations de leur l'environnement qu'à l'observation de la Lune. Ce calendrier était composé de 13 mois lunaires. Les saisons étaient au nombre de huit et étaient, elles aussi, très liées aux modifications apparentes de l'environnement. De nos jours, ce découpage calendaire n'a plus cours chez les Inuit, il a été remplacé par le calendrier grégorien.
Saisons Inuit
| Nom des mois lunaires |
Saisons |
| Siqinnaarut (Soleil possible) |
Ukiuq (hiver) |
| Quangattaasan (Soleil plus haut) |
Ukiuq (hiver) |
| Avunniit (bébés phoques prématurés) |
Upirngaksajaaq (vers le printemps) |
| Naittian (bébés phoques) |
Upirngaksaaq (début du printemps) |
| Tirigluit (bébés phoques à barbe) |
Upirngaaq (printemps) |
| Nurrait (bébés caribous) |
Upirngaaq (printemps) |
| Manniit (oeufs) |
Upirngaaq (printemps) |
| Saggaruut (les caribous perdent leurs poils) |
Aujaq (été) |
| Akullirut (le poil des caribous épaissit) |
Aujaq (été) |
| Amiraijaut (les bois des caribous perdent du duvet) |
Ukiatsajaaq (vers l'automne) |
| Ukuitlirut (début de l'hiver) |
Ukiaksaaq (automne) |
| Tusartuut (écoute nouvelles des voisins) |
Ukiaq (début de l'hiver) |
| Tauvigjuaq (grande obscurité) |
Ukiuq (hiver) |
Le tableau suivant donne la liste des treize mois lunaires et les saisons correspondantes.
Conclusion
 Conclusion
Conclusion
Dès l'époque d'Hipparque (environ 130 avant J.-C.) les astronomes eurent une assez bonne approximation de la valeur de l'année tropique. A la date de la création de notre calendrier en 1582, la valeur utilisée était pratiquement la même que celle déterminée par Al Battani sept siècles plus tôt. Les valeurs actuelles ne sont pas mesurées mais calculées à partir des théories planétaires et du mouvement de précession des équinoxes.
Dans de très nombreux pays le nombre des saisons est différent des quatre saisons astronomiques, cela en raison de l'importance des autres facteurs climatiques prépondérants dans ces régions.
Conclusion
 Conclusion
Conclusion
Les saisons astronomiques sont des phénomènes astronomiques simples produits par l'inclinaison l'axe de rotation de la Terre par rapport au plan de son orbite. Elles gouvernent en partie le climat sur Terre. Leurs longueurs sont différentes et évoluent avec le temps. Elles servent de repère dans la vie de tous les jours et sont à l'origine de notre calendrier.
 Prérequis
Prérequis Introduction
Introduction