Un spectre stellaire porte la signature des éléments constituant la photosphère de l'étoile.
Différents spectres stellaires.
Crédit :
ASM
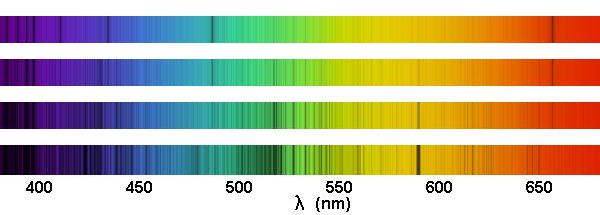
Un spectre stellaire porte la signature des éléments constituant la photosphère de l'étoile.
La spectroscopie, ou l'art de regarder les photons selon leur couleur, fut introduite à la fin du XIXe siècle, profitant de l'essor de la photographie.
du Cocher, observé à l'Observatoire de Paris en 1892 (pose de 1h20 !). Remarquer la juxtaposition d'un spectre de référence en émission.
Le spectre du soleil observé à très haute résolution spectrale présente de très nombreuses raies d'absorption. On remarque entre autres que la densité de raies spectrales est plus élevée dans le bleu que dans le rouge ; des raies telluriques dues à l'absorption dans l'atmosphère terrestre, se superposent aux raies stellaires, mais restent minoritaires.
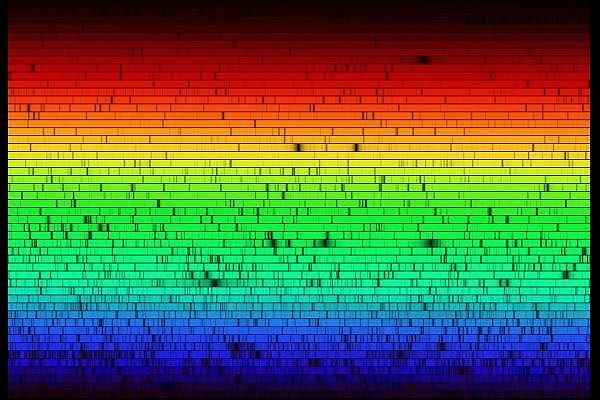
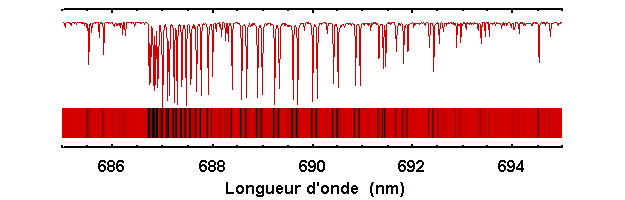
La modélisation d'un spectre nécessite la compréhension des conditions thermodynamique (température), mécanique (pression, en réponse au champ gravitationnel) et chimique (abondances) dans la photosphère stellaire, d'où sont issus les photons.
Toute la puissance de la spectrométrie réside dans cette finesse d'analyse, p.ex. pour aller dénicher à haute résolution spectrale de fines raies, et en sachant les interpréter.
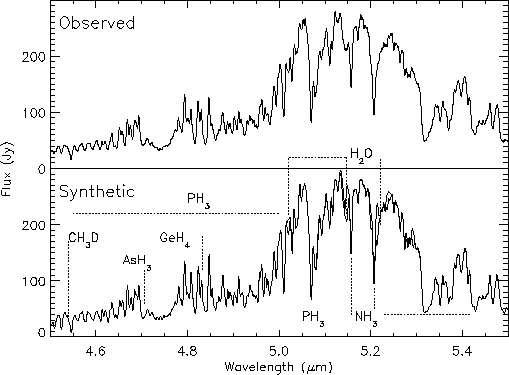
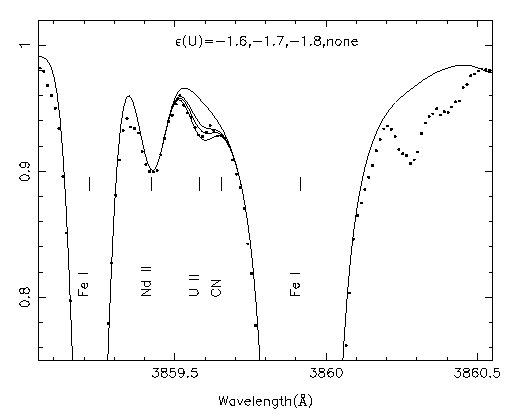
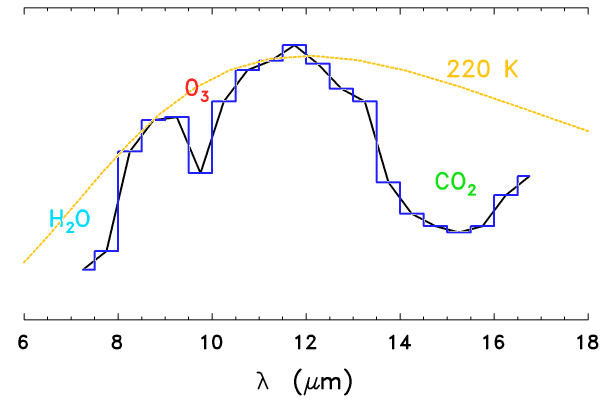
Un exemple illustre la puissance de l'information spectroscopique : une preuve de vie exoplanétaire serait apportée via l'étude spectrale IR, sensible à la présence d'ozone. L'ozone est liée à la présence d'oxygène, et donc à une chimie particulière qui est, au-moins dans un cas connu, propice à la vie.
ObjectifsUn cours complet de transfert de rayonnement, nécessaire pour comprendre les tenants et aboutissants du bon usage des données spectrométriques, est ici hors de propos, car trop complexe. Contentons-nous de récapituler quelques-uns des ingrédients qui permettent de comprendre un spectre.
On en déduit que l'interprétation d'un spectre apporte des informations sur les grandeurs qui précèdent : température, gravité, abondance des éléments.
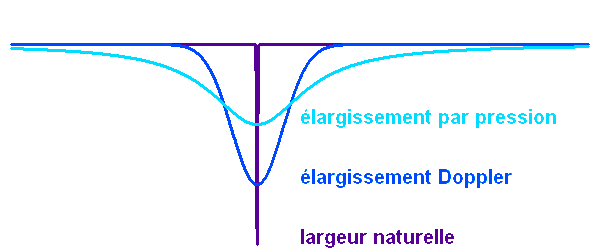
Dans l'atmosphère stellaire, deux phénomènes contribuent essentiellement à élargir les raies, conduisant à des largeurs bien supérieures à la largeur naturelle.
Si l'étoile est en rotation rapide, le profil de vitesse rotationnel est source d'un nouvel élargissement des raies, encore par effet Doppler .
Élargissement des raies spectralesDifficulté : ☆☆☆ Temps : 20 min
Déterminer la durée moyenne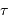 
entre deux collisions, en fonction du libre parcours moyen 
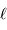(la distance moyenne entre 2 collisions) et de la vitesse moyenne des atome 
.
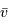[1 points]
Déterminer le libre parcours moyen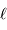 
d'un atome en fonction de la section efficace de collision 
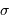et de la densité particulaire 
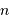. En déduire que le libre parcours moyen varie comme l'inverse de la masse volumique dans l'atmosphère de l'étoile.
[3 points]
On suppose que l'élargissement de la raie par pression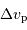 
varie comme 
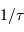, inverse de la durée moyenne entre 2 collisions. En déduire la dépendance de 
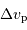en fonction de la température et de la masse volumique :
[2 points]
Montrer que, si l'élargissement des raies par pression est sensible, il permet, à type spectral donné, de distinguer les différentes classes stellaires.
[1 points]
L'hydrogène neutre est omniprésent dans l'Univers. Dans le milieu interstellaire, sa signature apparaît à diverses fréquence (visible, submillimétriques, radio...). La signature radio correspond à l'inversion du spin de l'électron : sa fréquence au repos vaut 1420 MHz, pour une longueur d'onde de 21 cm.
Raie H beta 
L'hydrogène est le constituant majoritaire des étoiles. La dépendance en température d'une raie de l'hydrogène apparaît clairement, pour des étoiles de type spectral chaud, beaucoup moins pour des températures d'équilibre plus basses. L'appliquette montre l'intervalle spectral correspondant à la raie H beta de l'hydrogène dans des étoiles de type A6 à K7 (température effective : 8000 à 4000 K). Le flux est normalisé à 1 dans le continu.
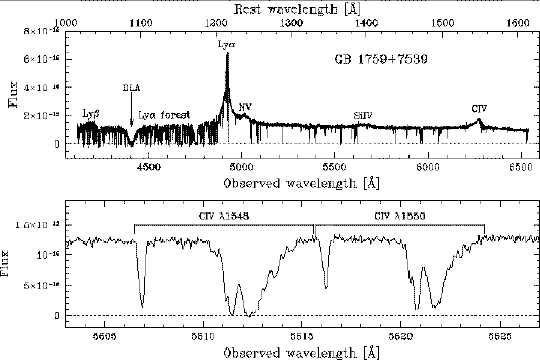
Des centaines de raies sont visibles dans le spectre d'un quasar éloigné, ce qui signe la présence sur la ligne de visée de matériel absorbant.
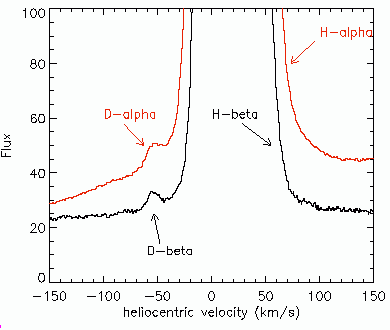
Les raies de Balmer du deutérium apparaissent au voisinage de celles de l'hydrogène.
Le décalage entre les raies de H et D est dû à un effet isotopique : l'électron n'a pas la même masse réduite autour du noyau de H (1 proton) et celui de D (de masse double, avec 1 proton et 1 neutron). [Rappel : la masse réduite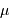 
est définie par
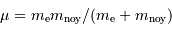, et s'approxime par 
].
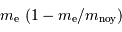Comme l'hydrogène représente presque 9 atomes sur 10 dans l'Univers, sa signature spectrale est omniprésente en absorption, en émission, dans diverses gammes du domaine spectral (raies de Balmer, raie à 21 cm...).
L'hydrogène du milieu interstellaire, sous forme moléculaire ou atomique froide, est à une température variant de 10 à 1000 K. L'hydrogène atomique neutre émet dans une fréquence radio particulière correspondant à la longueur d'onde 21 cm. L'intensité de la raie d'émission dépend de la densité totale d'hydrogène atomique neutre le long de la ligne de visée. La mesure de cette intensité de la raie observée permet donc de connaître la répartition bi-dimensionnelle des nuages d'hydrogène atomique.
Après l'hydrogène, l'hélium est le deuxième constituant le plus abondant dans l'Univers (environ 25%, par masse, soit 10% en concentration).
Mais la signature spectrale de l'hélium, gaz rare, est fort discrète. Comme l'hélium est difficilement ionisable, il faut une température élevée pour mettre en évidence les raies de l'hélium correspondant au spectre d'ionisation. En l'absence de moment dipolaire, l'atome He ne présente pas de spectre de vibration ni rotation.
pages_signatures-spectrales/signature-spectrale-sevaluer.html
Ce n'est qu'un peu de cinématique.
On peut s'en sortir par simple analyse dimensionnelle.
A partir de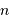 
, déterminer le volume moyen offert à un atome, et l'exprimer en fonction de 
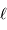et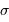 
.
Il suffit de se servir des résultats précédents exprimant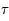 
en fonction des autres paramètres.
Le type spectral étant fixé, la température effective est également fixée.