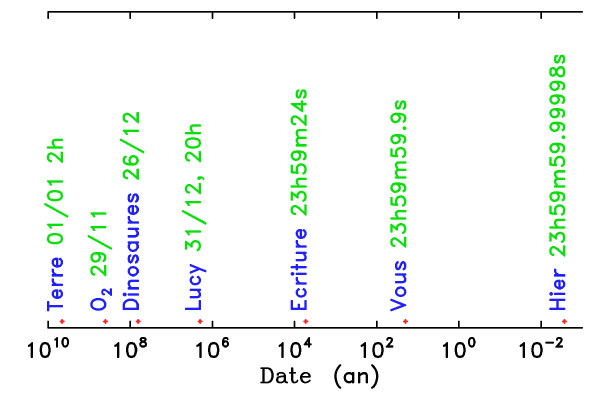
Rotation du ciel, ou de la Terre ? La régularité du mouvement en fait une "bonne" horloge.
Crédit :
CFHT
La rotation de la Terre
La mesure du temps, comme la définition des unités de temps, s'appuie sur des rotations régulières : la rotation propre de la Terre, sa révolution autour du Soleil.
Nombre de diviseurs de la base
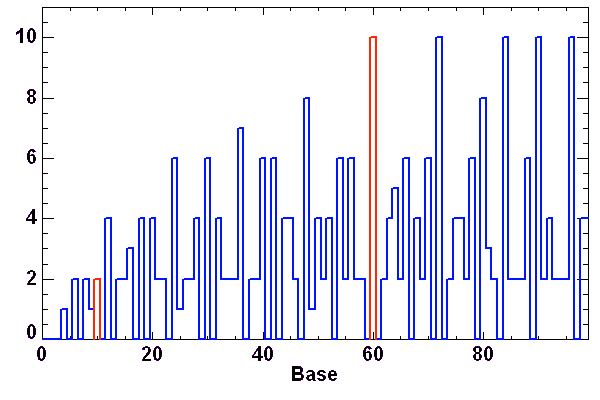
Le décompte du nombre de diviseurs de la base utilisée (1 et la base non compris) montre que 60 présente un maximum local prononcé, et que c'est le premier nombre à atteindre 10 diviseurs.
Crédit :
ASM
Heure, minute et seconde
La découpe des jours en 24 heures est une longue histoire... A l'époque où le temps n'était défini qu'à la précision d'une clepsydre ou d'un cadran solaire, la définition même de l'heure est restée vague, et sa durée variable.
Quantitativement, la base 24 provient des Egyptiens, pour qui 24 h = 12 h de jour + 12 h de
nuit, avec 12 = 1 + 10 + 1. Le jour et la nuit égyptiens comptaient
invariablement 10 heures, auxquelles étaient rajoutées 2 heures extrêmales
"entre chien et loup".
Pourquoi compte-t-on 60 secondes par minute, et 60 minutes par heure ?
Plus encore que pour l'heure, l'usage des minutes et secondes est récent (XVIIe siècle), vu qu'il nécessite un chronométrage précis du temps.
Quantitativement, la base 60 provient d'un héritage babylonien, et date de la fin du 3e millénaire avant notre ère. Le nombre 60 présente en effet l'avantage de posséder un grand nombre de diviseurs (2, 3, 4, 5, 6, 10, 12, 15, 20, 30), ce qui est commode pour les calculs de fraction lorsque les techniques de calcul d'une division ne sont pas connues.
C'est pour cette raison que 60 servait de base de calcul, en complément ou à la place de la base 10 ; cet usage a perduré de nos jours pour les mesures de temps et d'angles.
La mesure du temps
La mesure du temps s'est longtemps appuyée sur les mouvements les plus réguliers observables : la rotation propre de la Terre (le jour), sa révolution autour du Soleil (l'année). Ce n'est qu'en 1969 que le Bureau international des poids et mesures a abandonné la rotation de la Terre pour la définition de la seconde comme unité de temps.
La seconde correspond à l'intervalle de temps comprenant
9 192 631 770 oscillations entre les deux niveaux hyperfins de l'état fondamental de l'atome de césium 133.
Durées
Il n'y a pas d'unités temporelles spécifiques en astrophysique, contrairement aux nombreuses unités de distance.
La seconde apparaît une unité ni mieux ni moins bien appropriée que pour d'autres domaines que la physique.
L'année est de facto une unité pratique pour les problématiques circum-stellaires, vu qu'elle a été définie comme unité "circumsolaire".
Il suffit juste de s'habituer, dans certains cas, à l'usage des grands nombres, et de compter en millions, voire milliards d'années.
Temps de lumière
L'usage du temps de lumière est sans ambiguïté, dès lors que la célérité de la lumière est une constante universelle. Un temps de lumière est une distance, et correspond à la durée du trajet si l'on chevauche un photon.
 Définition
Définition
La célérité de la lumière dans le vide est un invariant, fixé par définition à 299 792 458 m/s.
 Echelle de temps dynamique
Echelle de temps dynamique
Difficulté : ☆☆
Temps : 20 min
On considère un objet autogravitant de masse 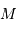 , rayon
, rayon 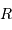 , et on s'intéresse à son échelle de temps dynamique.
, et on s'intéresse à son échelle de temps dynamique.
Question 1)
Quelle constante fondamentale de la physique intervient nécessairement dans toute formulation de la physique du problème.
Il s'agit ici de gravitation.
Question 2)
Montrer, avec le minimum de calcul possible, que 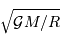 est homogène à une vitesse, et en déduire que
est homogène à une vitesse, et en déduire que 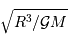 est homogène à un temps.
est homogène à un temps.
Essayez de dénicher une loi physique qui exprime une vitesse dans un problème gouverné par la gravitation.
L'accélération normale d'un satellite en orbite circulaire peut s'écrire en fonction du champ gravitationnel, à la distance 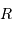 :
:
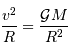
Question 3)
Montrer que 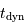 peut s'exprimer en fonction de la masse volumique moyenne
peut s'exprimer en fonction de la masse volumique moyenne 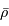 de l'objet.
de l'objet.
 La vie du Soleil en 1 an seulement
La vie du Soleil en 1 an seulement
Difficulté : ☆
Temps : 30 min
Quelques événements
| La formation du système solaire | en 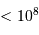 an après le Soleil an après le Soleil |
| L'apparition du dioxygène atmosphérique | 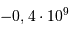 an an |
| La disparition des dinosaures | 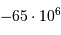 an an |
| Notre ancêtre Lucy | 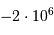 an an |
| La maîtrise de l'écriture | 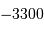 avant JC avant JC |
| Votre naissance | ... |
| Hier | |
Question 1)
Reporter dans un graphe en échelle logarithmique les
événements suivants de l'histoire de la Terre depuis la naissance du Soleil [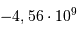 an].
an].
Déterminer leur date, sur la base d'une année, la formation du Soleil débutant le 1er janvier à 0 heure, et aujourd'hui correspondant à minuit du 31 décembre.
Aller chercher une calculatrice !
 Durée d'effondrement
Durée d'effondrement
Difficulté : ☆☆
Temps : 20 min
L'échelle de temps dynamique d'un objet autogravitant donne un bon ordre de grandeur de la durée caractéristique de l'éventuel effondrement de cet objet.
| Masse (kg) | Rayon (km) |
| Soleil | 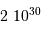 | 700 000 |
| Étoile à neutrons | 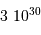 | 10 |
| Nuage d'hydrogène moléculaire | 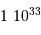 | 10 AL |
Question 1)
Rappeler l'expression de cette échelle de temps, fonction de la
masse 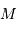 , du rayon
, du rayon 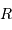 et de la constante gravitationnelle
et de la constante gravitationnelle 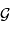 .
.
[2 points]
Question 2)
Calculer l'échelle de temps pour les 3 objets proposés. Commenter.
[3 points]
 Quelle source d'énergie ?
Quelle source d'énergie ?
Difficulté : ☆☆
Temps : 20 min
Question 2)
En déduire l'échelle de temps associée à ce réservoir d'énergie. Est-elle compatible avec l'âge du Soleil ?
[2 points]
Question 3)
On s'intéresse au réservoir d'énergie nucléaire. Le rendement énergétique de la fusion de l'hydrogène en hélium est de 0.007, ce qui signifie que la fusion d'une masse 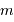 d'hydrogène dégage une énergie
d'hydrogène dégage une énergie 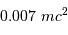 . On estime, pour une étoile telle que le Soleil, qu'un dixième seulement de sa masse fusionnera.
En déduire une estimation de la durée de vie du Soleil.
. On estime, pour une étoile telle que le Soleil, qu'un dixième seulement de sa masse fusionnera.
En déduire une estimation de la durée de vie du Soleil.
[2 points]
- Question 1
Aide :
Il s'agit ici de gravitation.
Solution :
Dès lors que l'on parle de la gravitation, intervient la constante gravitationnelle 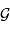 .
.
- Question 2
Aide :
Essayez de dénicher une loi physique qui exprime une vitesse dans un problème gouverné par la gravitation.
Aide :
L'accélération normale d'un satellite en orbite circulaire peut s'écrire en fonction du champ gravitationnel, à la distance 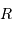 :
:
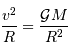
Solution :
Il est plus simple de procéder par induction, plutôt que de chercher des exposants 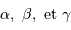 qui satisfassent à :
qui satisfassent à :
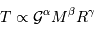
On écrit p.ex. que l'accélération normale d'un satellite en orbite circulaire à la distance 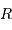 est égale au champ gravitationnel :
est égale au champ gravitationnel :
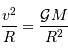
D'où il sort une vitesse caractéristique (que l'on rencontre dans tout problème gravitationnel, à une constante numérique près que l'analyse dimensionnelle ne permet pas de calculer)
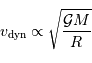
Le temps dynamique ne peut être que de la forme
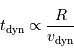
et donc
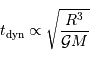
- Question 3
Aide :
Définir 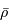 en fonction de
en fonction de 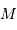 et
et 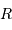
Solution :
La masse volumique moyenne est proportionnelle à la masse 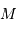 divisée par le volume
divisée par le volume 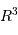 :
:
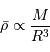
et donc le temps dynamique s'exprime :
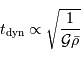
- Question 4
Aide :
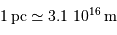
Solution :
Les application numériques donnent :
- noyau cométaire : 31 400 s, soit presque 9 h
- la Terre : 5100 s, soit 1h 25min
- la Voie Lactée : 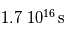 , soit environ 500 millions d'années
, soit environ 500 millions d'années
La constante de temps dynamique d'un noyau cométaire est plus longue que celle de la Terre, car la masse volumique moyenne 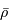 est plus faible.
est plus faible.
La constante de temps dynamique d'une galaxie représente une fraction non négligeable de l'âge de l'Univers. Elle donne l'ordre de grandeur de sa période de rotation moyenne.
La constance de temps dynamique pour la Terre représente l'ordre de grandeur d'une foultitude de phénomènes :
- la période typique d'un satellite en orbite basse (1h40 en fait)
- la durée typique d'un vol de missile balistique
- la durée typique de propagation d'une secousse sismique de l'épicentre du séisme aux antipodes
- un match de foot... mais ça c'est un hasard


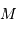 et rayon
et rayon 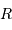 , un phénomène gouverné par la gravitation aura naturellement une constante de temps de l'ordre de
, un phénomène gouverné par la gravitation aura naturellement une constante de temps de l'ordre de 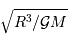 (vérification proposée en
(vérification proposée en 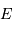 et
émettant une luminosité totale (càd une puissance)
et
émettant une luminosité totale (càd une puissance) 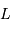 peut le faire pendant typiquement la durée
peut le faire pendant typiquement la durée 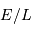 .
.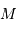 , rayon
, rayon 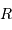 , et on s'intéresse à son échelle de temps dynamique.
, et on s'intéresse à son échelle de temps dynamique.
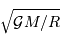 est homogène à une vitesse, et en déduire que
est homogène à une vitesse, et en déduire que 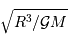 est homogène à un temps.
est homogène à un temps.
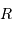 :
:
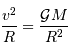
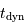 peut s'exprimer en fonction de la masse volumique moyenne
peut s'exprimer en fonction de la masse volumique moyenne 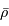 de l'objet.
de l'objet.
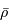 en fonction de
en fonction de 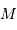 et
et 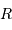
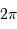 :
:
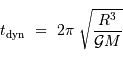
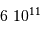
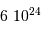
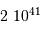
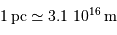
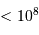 an après le Soleil
an après le Soleil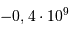 an
an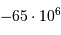 an
an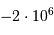 an
an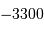 avant JC
avant JC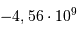 an].
an].
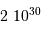
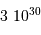
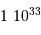
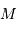 , du rayon
, du rayon 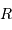 et de la constante gravitationnelle
et de la constante gravitationnelle 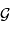 .
.
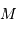 , du rayon
, du rayon 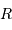 du Soleil, et de la constante gravitationnelle
du Soleil, et de la constante gravitationnelle 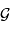 . Faire l'application numérique.
. Faire l'application numérique.
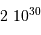
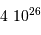
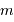 d'hydrogène dégage une énergie
d'hydrogène dégage une énergie 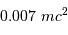 . On estime, pour une étoile telle que le Soleil, qu'un dixième seulement de sa masse fusionnera.
En déduire une estimation de la durée de vie du Soleil.
. On estime, pour une étoile telle que le Soleil, qu'un dixième seulement de sa masse fusionnera.
En déduire une estimation de la durée de vie du Soleil.
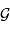 .
.
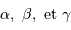 qui satisfassent à :
qui satisfassent à :
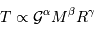
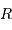 est égale au champ gravitationnel :
est égale au champ gravitationnel :
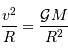
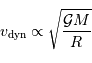
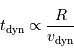
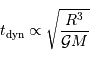
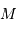 divisée par le volume
divisée par le volume 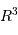 :
:
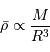
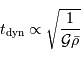
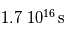 , soit environ 500 millions d'années
, soit environ 500 millions d'années
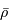 est plus faible.
est plus faible.