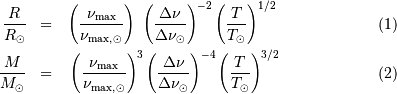Objectifs
Objectifs
Définir dans quelles conditions la fusion de l'hydrogène va s'amorcer.
 Prérequis
Prérequis
Pression au centre de l'étoile.
La compression gravitationnelle peut être équilibrée par 3 termes de
pression :
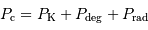
respectivement pression du gaz de matière chaud, pression de Fermi et présence du gaz de photons.
Phase de contraction
La compression gravitationnelle au centre de l'objet varie en fonction de sa masse et de son rayon comme :
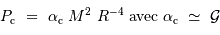
Lors de la contraction de l'objet, la température centrale varie en fonction du rayon  comme :
comme :
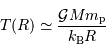
(avec 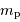 la masse du proton).
Lorsque
la masse du proton).
Lorsque 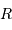 décroît, la température augmente, et la pression aussi.
La température limite d'enclenchement des réactions nucléaires peut-elle être atteinte ?
décroît, la température augmente, et la pression aussi.
La température limite d'enclenchement des réactions nucléaires peut-elle être atteinte ?
Rôle des différents termes de pression
La pression cinétique présente la même dépendance en masse et rayon que la compression gravitationnelle :
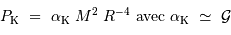
Avec ces variables, la pression de dégénérescence varie elle comme :
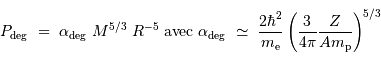
Lorsque l'objet se contracte, cette pression augmente plus vite que la compression gravitationnelle. Elle peut donc bloquer la compression, en atteignant un équilibre caractérisé par :
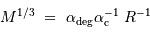
Température centrale
Dans ces conditions, la température atteinte au centre vaut (en éliminant la variable rayon des équations qui précèdent) :
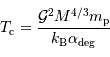
Si la température centrale atteint 10 millions de Kelvin, une étoile est née. Sinon, il s'agit d'un astre dégénéré sans amorçage des réactions nucléaires.
Masse minimale
Il est nécessaire d'avoir une masse initiale suffisante pour atteindre une température permettant d'initier la fusion de l'hydrogène. Un modèle précis donne la masse minimale pour la combustion de l'hydrogène :
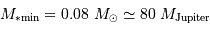
Entre 13 et 80 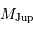 , l'objet ne peut brûler que son deutérium : il s'agit alors d'une naine brune.
, l'objet ne peut brûler que son deutérium : il s'agit alors d'une naine brune.
Masse maximale
La pression de radiation varie comme 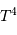 , donc :
, donc :
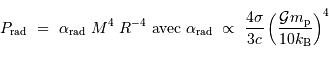
à comparer à la compression gravitationnelle 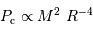 .
.
Si la masse est trop importante, la pression de radiation va conduire à souffler l'étoile. La limite d'équilibre 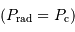 est atteinte lorsque :
est atteinte lorsque :
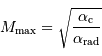
Une modélisation précise donne la valeur numérique :
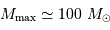
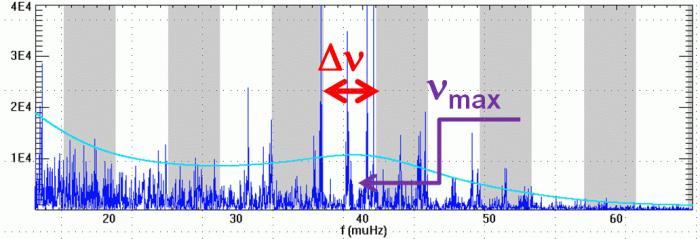
Définition des fréquences caractéristiques
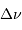
et
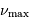
d'un
spectre d'oscillation stellaire.
Crédit :
ASM
 Masse et rayon sismiques
Masse et rayon sismiques
Difficulté : ☆☆
Temps : 30 min
L'astérosismologie, l'étude de la vibration des étoiles, est une
branche récente de la physique stellaire qui apporte de nouvelles
observables. La description globale d'un
spectre d'oscillation introduit
deux fréquences caractéristiques 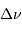 et
et 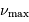 ,
respectivement appelées grande séparation et fréquence du maximum
de signal sismique. Elles dépendent de la masse
,
respectivement appelées grande séparation et fréquence du maximum
de signal sismique. Elles dépendent de la masse 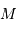 , du rayon
, du rayon 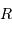 et de la température effective
et de la température effective 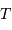 de l'étoile via les définitions :
de l'étoile via les définitions :
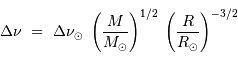
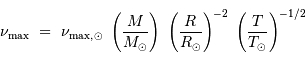
avec les valeurs solaires 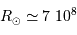 m,
m, 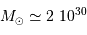 kg,
kg, 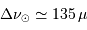 Hz,
Hz, 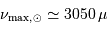 Hz, et
Hz, et 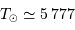 K.
K.
Question 1)
Ordonner les valeurs de 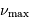 pour deux étoiles de même type
spectral mais présentant un champ gravitationnel très différent.
pour deux étoiles de même type
spectral mais présentant un champ gravitationnel très différent.
[2 points]
Identifier dans l'expression de 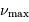 ce qui peut ressemble au
champ gravitationnel d'une étoile.
ce qui peut ressemble au
champ gravitationnel d'une étoile.
Comment se traduit le fait que l'on considère des étoiles de même
type spectral ?
Question 2)
Quelle mesure intéressante apporte 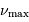 , grandeur mesurée à
une précision de l'ordre de quelques pourcents ?
, grandeur mesurée à
une précision de l'ordre de quelques pourcents ?
[1 points]
La réponse est quasiment à la question précédente.
Question 3)
Ordonner les valeurs de la grande séparation 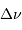 pour deux
étoiles présentant une masse volumique moyenne très différente.
pour deux
étoiles présentant une masse volumique moyenne très différente.
[1 points]
Exprimer la masse volumique moyenne en fonction des masse et
rayon stellaire.
Quel lien entre 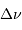 et la masse volumique moyenne ?
et la masse volumique moyenne ?
Question 4)
Calculer 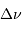 et
et 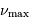 pour une géante rouge, de masse égale
à la masse du Soleil, de rayon égal à
pour une géante rouge, de masse égale
à la masse du Soleil, de rayon égal à 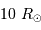 et de température
effective 4 800 K.
et de température
effective 4 800 K.
[1 points]
Faites chauffer le calcotron.
Question 5)
Montrer que l'on peut déduire de la mesure de 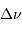 ,
, 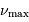 et
et
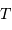 une estimation des masse et rayon stellaires. Donner ces
expressions ; les exprimer en fonction des valeurs solaires.
une estimation des masse et rayon stellaires. Donner ces
expressions ; les exprimer en fonction des valeurs solaires.
[2 points]
Désolé, pas d'autre solution que retrousser ses manches et
inverser les équations de départ !
Question 6)
Énoncer un des intérêts de l'astérosismologie ?
[1 points]
 De nouvelles classes spectrales ?
De nouvelles classes spectrales ?
Difficulté : ☆☆
Temps : 5 min
Question 1)
Pourquoi peut-on penser qu'il n'y aura pas de découvertes de nouvelles classes spectrales
même si l'on met en service de nouveaux télescopes de sensibilité encore plus grande ?
Si l'on découvrait de nouvelles classes, correspondraient-elles à des étoiles très ou très peu lumineuses ?
- Question 1
Aide :
Identifier dans l'expression de 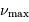 ce qui peut ressemble au
champ gravitationnel d'une étoile.
ce qui peut ressemble au
champ gravitationnel d'une étoile.
Aide :
Comment se traduit le fait que l'on considère des étoiles de même
type spectral ?
Solution :
Le champ gravitationnel d'une étoile varie en 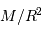 , comme
, comme
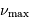 , dont l'expression comporte juste une dépendance
supplémentaire en fonction de la température. Comme le type
spectral est supposé fixé, cette dépendance est donc transparente,
et
, dont l'expression comporte juste une dépendance
supplémentaire en fonction de la température. Comme le type
spectral est supposé fixé, cette dépendance est donc transparente,
et 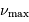 porte la même information que le champ gravitationnel,
et réciproquement. On en déduit qu'une étoile de champ
gravitationnel plus intense présente un spectre avec une fréquence
porte la même information que le champ gravitationnel,
et réciproquement. On en déduit qu'une étoile de champ
gravitationnel plus intense présente un spectre avec une fréquence
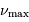 plus élevée, et réciproquement.
plus élevée, et réciproquement.
- Question 2
Aide :
La réponse est quasiment à la question précédente.
Solution :
La mesure de 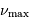 , identifiée à partir du spectre
d'oscillation, permet une estimation précise du champ
gravitationnel à la surface de l'étoile.
, identifiée à partir du spectre
d'oscillation, permet une estimation précise du champ
gravitationnel à la surface de l'étoile.
- Question 3
Aide :
Exprimer la masse volumique moyenne en fonction des masse et
rayon stellaire.
Aide :
Quel lien entre 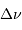 et la masse volumique moyenne ?
et la masse volumique moyenne ?
Solution :
L'examen de la définition de 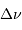 montre que cette fréquence
varie comme la racine carrée de la masse volumique de l'étoile.
Une étoile peu dense présentera donc une plus petite valeur de
montre que cette fréquence
varie comme la racine carrée de la masse volumique de l'étoile.
Une étoile peu dense présentera donc une plus petite valeur de
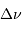 qu'une étoile plus dense.
qu'une étoile plus dense.
- Question 4
Aide :
Faites chauffer le calcotron.
Solution :
La géante, 10 fois plus grande que le Soleil, présente un volume
1000 fois plus important, donc une densité 31 fois moindre, et
donc 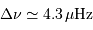 . Pour
. Pour 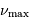 , l'application
numérique donne
, l'application
numérique donne 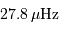 .
.
- Question 5
Aide :
Désolé, pas d'autre solution que retrousser ses manches et
inverser les équations de départ !
Solution :
L'inversion donne :
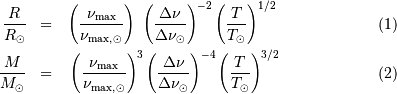
- Question 6
Solution :
Ce n'est pas tous les jours qu'une technique observationnelle
donne accès à la masse et au rayon de l'étoile relativement
précisément, et indépendamment de toute mesure de distance !
 Objectifs
Objectifs Prérequis
Prérequis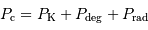
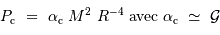
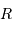 comme :
comme :
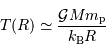
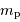 la masse du proton).
Lorsque
la masse du proton).
Lorsque 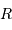 décroît, la température augmente, et la pression aussi.
La température limite d'enclenchement des réactions nucléaires peut-elle être atteinte ?
décroît, la température augmente, et la pression aussi.
La température limite d'enclenchement des réactions nucléaires peut-elle être atteinte ?
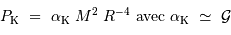
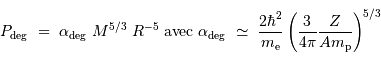
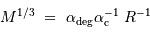
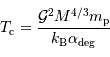
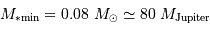
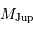 , l'objet ne peut brûler que son deutérium : il s'agit alors d'une naine brune.
, l'objet ne peut brûler que son deutérium : il s'agit alors d'une naine brune.
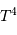 , donc :
, donc :
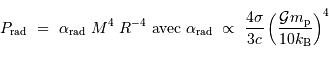
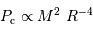 .
.
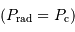 est atteinte lorsque :
est atteinte lorsque :
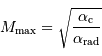
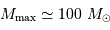

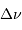 et
et 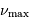 d'un
spectre d'oscillation stellaire.
d'un
spectre d'oscillation stellaire.
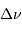 et
et 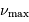 ,
respectivement appelées grande séparation et fréquence du maximum
de signal sismique. Elles dépendent de la masse
,
respectivement appelées grande séparation et fréquence du maximum
de signal sismique. Elles dépendent de la masse 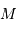 , du rayon
, du rayon 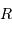 et de la température effective
et de la température effective 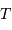 de l'étoile via les définitions :
de l'étoile via les définitions :
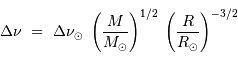
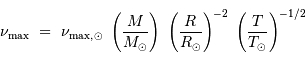
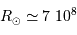 m,
m, 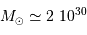 kg,
kg,  Hz,
Hz, 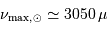 Hz, et
Hz, et 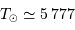 K.
K.
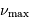 pour deux étoiles de même type
spectral mais présentant un champ gravitationnel très différent.
pour deux étoiles de même type
spectral mais présentant un champ gravitationnel très différent.
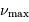 ce qui peut ressemble au
champ gravitationnel d'une étoile.
ce qui peut ressemble au
champ gravitationnel d'une étoile.
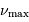 , grandeur mesurée à
une précision de l'ordre de quelques pourcents ?
, grandeur mesurée à
une précision de l'ordre de quelques pourcents ?
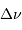 pour deux
étoiles présentant une masse volumique moyenne très différente.
pour deux
étoiles présentant une masse volumique moyenne très différente.
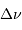 et la masse volumique moyenne ?
et la masse volumique moyenne ?
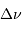 et
et 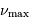 pour une géante rouge, de masse égale
à la masse du Soleil, de rayon égal à
pour une géante rouge, de masse égale
à la masse du Soleil, de rayon égal à 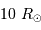 et de température
effective 4 800 K.
et de température
effective 4 800 K.
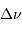 ,
, 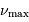 et
et
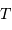 une estimation des masse et rayon stellaires. Donner ces
expressions ; les exprimer en fonction des valeurs solaires.
une estimation des masse et rayon stellaires. Donner ces
expressions ; les exprimer en fonction des valeurs solaires.
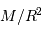 , comme
, comme
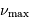 , dont l'expression comporte juste une dépendance
supplémentaire en fonction de la température. Comme le type
spectral est supposé fixé, cette dépendance est donc transparente,
et
, dont l'expression comporte juste une dépendance
supplémentaire en fonction de la température. Comme le type
spectral est supposé fixé, cette dépendance est donc transparente,
et 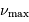 porte la même information que le champ gravitationnel,
et réciproquement. On en déduit qu'une étoile de champ
gravitationnel plus intense présente un spectre avec une fréquence
porte la même information que le champ gravitationnel,
et réciproquement. On en déduit qu'une étoile de champ
gravitationnel plus intense présente un spectre avec une fréquence
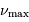 plus élevée, et réciproquement.
plus élevée, et réciproquement.
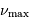 , identifiée à partir du spectre
d'oscillation, permet une estimation précise du champ
gravitationnel à la surface de l'étoile.
, identifiée à partir du spectre
d'oscillation, permet une estimation précise du champ
gravitationnel à la surface de l'étoile.
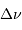 montre que cette fréquence
varie comme la racine carrée de la masse volumique de l'étoile.
Une étoile peu dense présentera donc une plus petite valeur de
montre que cette fréquence
varie comme la racine carrée de la masse volumique de l'étoile.
Une étoile peu dense présentera donc une plus petite valeur de
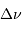 qu'une étoile plus dense.
qu'une étoile plus dense.
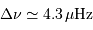 . Pour
. Pour 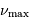 , l'application
numérique donne
, l'application
numérique donne 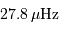 .
.