L'observation des étoiles binaires visuelles est limitée par la qualité d'image des observations au sol. La plus petite séparation angulaire détectable depuis le sol est d'environ 1 seconde d'arc. Cette limite imposée par la turbulence atmosphérique est améliorée grâce à l'optique adaptative. L'interférométrie sur les VLT permet d'atteindre une séparation de quelques millièmes de seconde d'arc.
L'effet de sélection dans l'observation de ces couples est très important. Deux catégories d'objets sont en particulier très difficile à observer : les binaires à longue période d'une part, et d'autre part les étoiles qui forment au contraire un système très serré.
La séparation caractéristique de tels couples varie d'une fraction d'unité astronomique à quelques centaines d'unités astronomiques, quand leurs périodes s'échelonnent de quelques années à plus d'un siècle. Les périodes plus longues (quelques siècles) ou les orbites plus grandes sont très difficiles à mettre en évidence, essentiellement pour des raisons de recul dans le temps.
Un grand intérêt de l'observation des étoiles binaires visuelles est que la mesure des paramètres apparents de l'orbite permet de calculer la masse des deux composantes du système, via la 3e loi de Kepler :
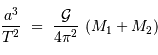
La définition du barycentre du système conduit à :
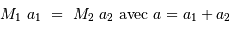
où 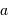 représente le demi-grand axe de l'orbite relative du corps de masse
représente le demi-grand axe de l'orbite relative du corps de masse 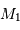 par rapport au corps de masse
par rapport au corps de masse 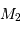 et
et 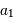 et
et 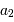 sont les demi-grands axes des orbites absolues de chacun des corps par rapport au barycentre
sont les demi-grands axes des orbites absolues de chacun des corps par rapport au barycentre 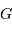 du système.
du système.
La mesure de 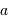 ,
, 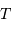 et de la position du barycentre du système (c'est-à-dire des demi-grands axes
et de la position du barycentre du système (c'est-à-dire des demi-grands axes 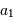 et
et 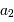 ) permet alors de déterminer
) permet alors de déterminer 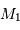 et
et 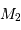 .
.
Difficulté : ☆ Temps : 30 min
On observe une étoile double visuelle dont les caractéristiques observées sont les suivantes :
| séparation angulaire maximum | 5" |
| séparation angulaire minimum | 1" |
parallaxe 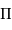 | 0.1" |
période de révolution 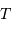 | 30 ans |
L'étoile primaire 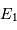 se trouve au foyer de l'orbite observée ; le compagnon est observé à une distance du barycentre 5 fois plus grande que celle de l'étoile primaire.
se trouve au foyer de l'orbite observée ; le compagnon est observé à une distance du barycentre 5 fois plus grande que celle de l'étoile primaire.
Montrer que l'inclinaison  du plan de l'orbite est nulle.
du plan de l'orbite est nulle.
Déterminer le rapport des masses des deux étoiles.
Exprimer la loi du mouvement des deux corps (troisième loi de Kepler) en prenant comme unités de masse, la masse du Soleil, de temps, l'année, et de distance, la distance Terre-Soleil (unité astronomique).
Calculer la distance en parsec à partir de la parallaxe, puis le demi-grand axe en UA.
Déterminer la masse de chaque composante en unité de masse solaire.
Dans le cas des binaires visuelles, on observe à chaque instant la séparation angulaire apparente 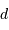 entre les deux composantes et l'angle de position
entre les deux composantes et l'angle de position 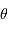 de la composante la plus faible par rapport à une direction de référence (celle de la direction du pôle céleste Nord) passant par l'étoile la plus brillante et repérée par rapport aux autres étoiles.
de la composante la plus faible par rapport à une direction de référence (celle de la direction du pôle céleste Nord) passant par l'étoile la plus brillante et repérée par rapport aux autres étoiles.
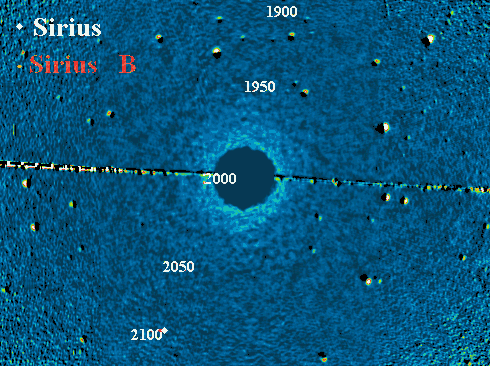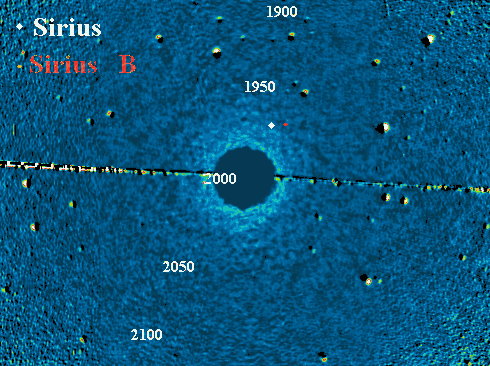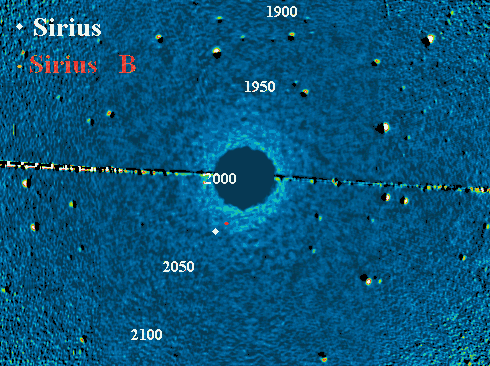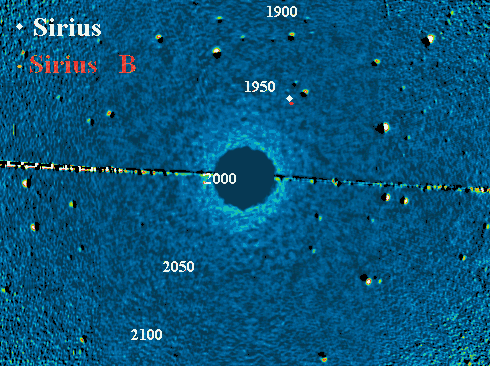
Trajectoire apparente de Sirius B autour de Sirius A, et animation correspondante.
Ce que voit en général l'observateur, ce n'est pas l'orbite elle-même mais sa projection sur un plan perpendiculaire à la ligne de visée. Dans cette projection, les orbites sont toujours des ellipses et la loi des aires est conservée. Par contre, le foyer de l'ellipse projetée (ou orbite apparente) n'est pas la projection du foyer de l'orbite vraie et le demi-grand axe apparent n'est pas non plus la projection du demi-grand axe vrai. Pour remonter aux paramètres de l'orbite réelle, il est donc nécessaire de reconstituer cette orbite à partir de l'ellipse observée.
Reconstituer les éléments géométriques de l'orbite vraie du système.
Eléments géométriques définissant une trajectoire elliptique.
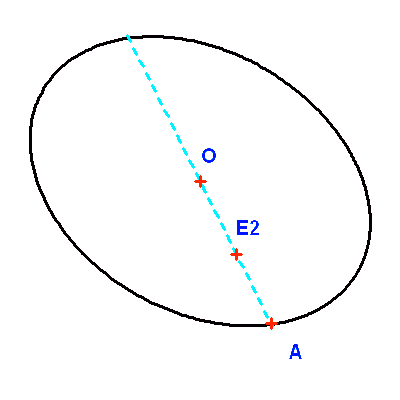
L'observation donne une série de positions relatives des deux étoiles sur le ciel. En choisissant l'étoile la plus brillante (E2) comme origine des coordonnées, les positions de l'étoile la plus faible (E1) s'agencent sur une ellipse, mais il apparaît que E2 n'est pas au foyer de l'orbite projetée.

Soit O le centre de l'ellipse apparente et A à l'intersection de la droite OE2 avec l'ellipse, au plus proche de E2 ; O est la projection du centre de l'orbite vraie et A est la projection de son périgée. Le segment [OA] est alors la projection du demi-grand axe de l'orbite vraie.
L'excentricité 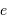 n'est pas plus conservée par la projection que le demi-grand axe, mais la détermination de l'excentricité de l'orbite réelle découle directement des paramètres de l'orbite projetée. Cette excentricité est en effet définie par la distance du foyer (E2) au centre (O), rapportée au demi-grand axe (0A). Ce rapport se mesure directement par OE2/OA, qui est conservé par la projection (par application du théorème de Thalès).
n'est pas plus conservée par la projection que le demi-grand axe, mais la détermination de l'excentricité de l'orbite réelle découle directement des paramètres de l'orbite projetée. Cette excentricité est en effet définie par la distance du foyer (E2) au centre (O), rapportée au demi-grand axe (0A). Ce rapport se mesure directement par OE2/OA, qui est conservé par la projection (par application du théorème de Thalès).
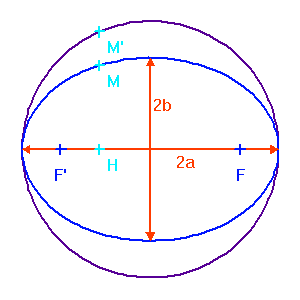
On retrouve l'inclinaison  de l'orbite vraie avec le plan du
ciel en reconstituant la projection du cercle principal de
l'ellipse vraie : ce cercle se projette suivant une ellipse dont
le rapport d'axes est égal à
de l'orbite vraie avec le plan du
ciel en reconstituant la projection du cercle principal de
l'ellipse vraie : ce cercle se projette suivant une ellipse dont
le rapport d'axes est égal à 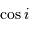 .
.
On utilise pour cela une propriété de l'ellipse et de son cercle
principal : la direction parallèle au diamètre conjugué du grand
axe passant par un point 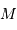 de l'ellipse coupe le cercle
principal en un point
de l'ellipse coupe le cercle
principal en un point 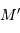 et le grand axe en un point
et le grand axe en un point 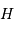 , tels
que
, tels
que 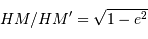 . Cette propriété se conservant par
projection on peut donc reconstituer l'ellipse projection du
cercle principal point par point à partir de la trajectoire
observée et de la direction conjuguée, i.e. la direction de la
tangente à l'ellipse observée aux points
. Cette propriété se conservant par
projection on peut donc reconstituer l'ellipse projection du
cercle principal point par point à partir de la trajectoire
observée et de la direction conjuguée, i.e. la direction de la
tangente à l'ellipse observée aux points 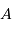 et
et 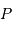 .
.
Le
demi-grand axe de l'orbite vraie est donc finalement égal à
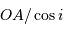 .
.
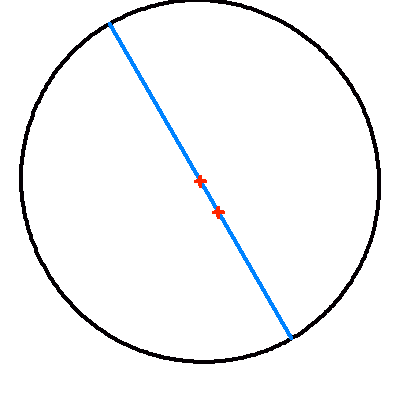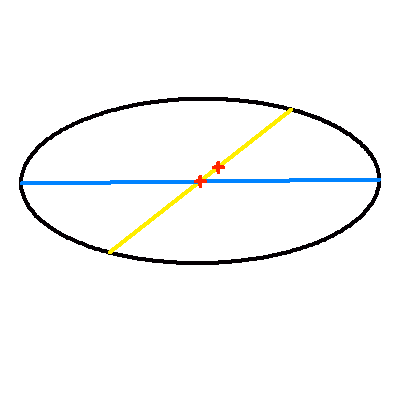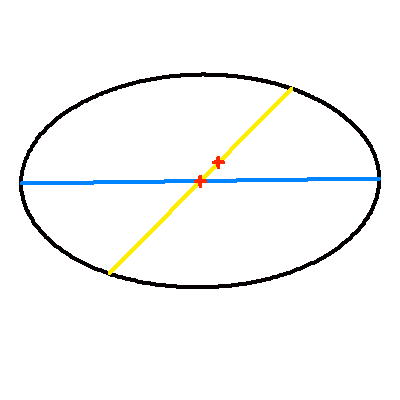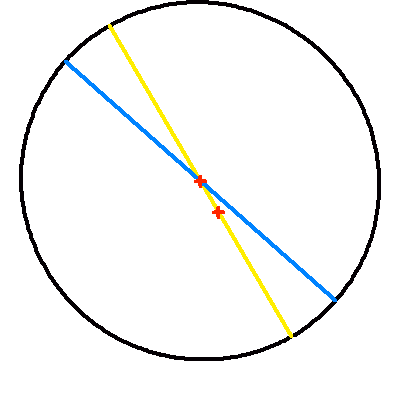
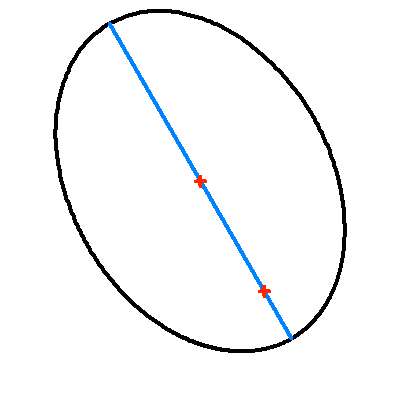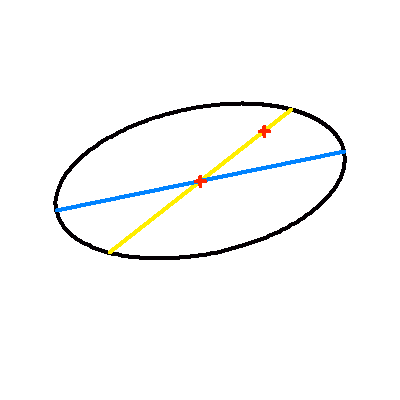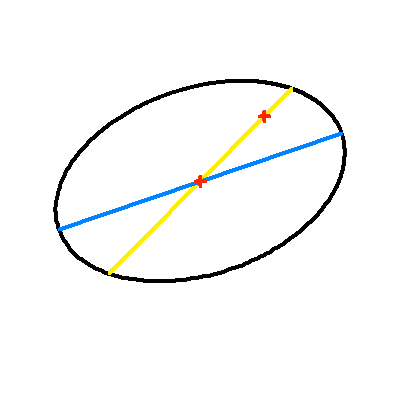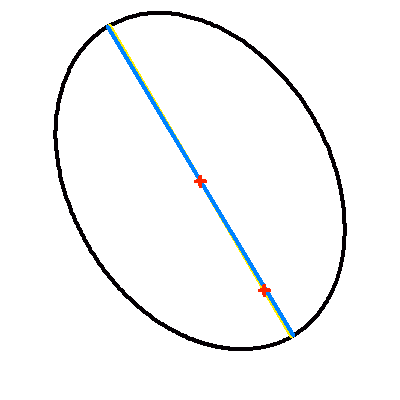
La projection du plan de l'orbite sur le plan du ciel modifie les paramètres de l'orbite apparente. Si le centre de l'ellipse est conservé par projection (la projection du centre de l'ellipse est égale au centre de l'ellipse projeté), le foyer ne l'est point : le demi-grand axe apparent se distingue (sauf dans certains cas très particuliers) de la projection du demi-grand axe.
L'animation met ce phénomène en évidence : elle montre l'apparence de la projection dans le plan du ciel d'une orbite elliptique, pour différentes inclinaisons. Étonnamment, l'effet est moins marqué dans le cas d'une excentricité plus grande.

L'appliquette donne la position de Sirius B par rapport à Sirius A.
Difficulté : ☆☆ Temps : 30 min
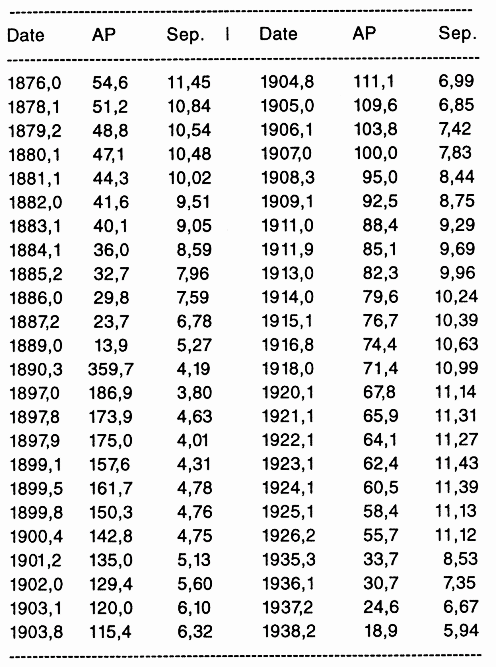
En 1844, F.W. Bessel découvrit que Sirius présentait un mouvement propre, non linéaire, mais dont la modulation ressemblait à celle d'une étoile double visuelle. Il en conclut que le mouvement propre de Sirius était affecté par l'interaction gravitationnelle avec une seconde étoile de luminosité trop faible pour être observée. Ce compagnon fut observé pour la première fois en 1862 par A.G. Clark : cette étoile appelée Sirius B a une magnitude de 8.7 alors que celle de Sirius A vaut -1.4.

| demi-grand axe | 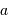 | 7.24" |
| excentricité | 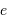 | 0.765 |
| distance entre les foyers | 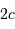 | 11.08" |
Sirius A, à l'intersection des axes, est-il au foyer de l'ellipse apparente ? Quelle conséquence en tire-t-on pour le plan de l'orbite ?
[1 points]
Déterminer la valeur de la période (en années).
[1 points]
Déterminer graphiquement le grand axe de l'ellipse vraie (il contient le centre de l'ellipse projetée (le centre est conservé par projection) et bien sûr Sirius A). Déterminer les positions apparentes P et A du périastre et de l'apoastre et les dates qui leur correspondent.
[2 points]
Déterminer l'excentricité de l'orbite vraie.
[1 points]
Difficulté : ☆☆ Temps : 30 min

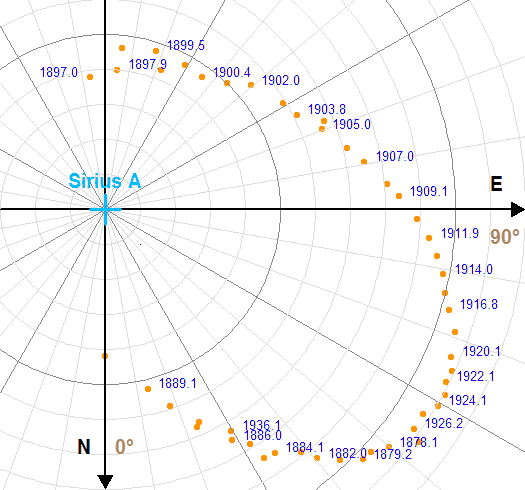
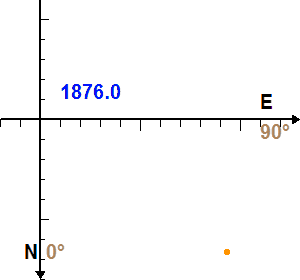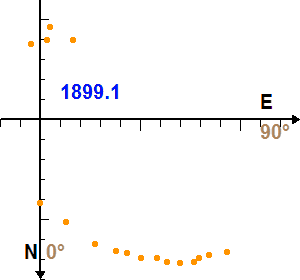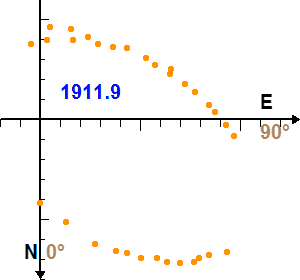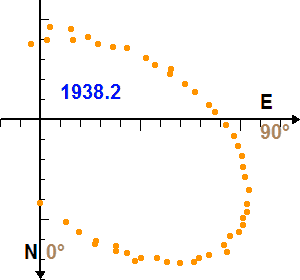
La figure trace le mouvement vrai de la composante Sirius B par rapport à Sirius A dans le plan orbital.
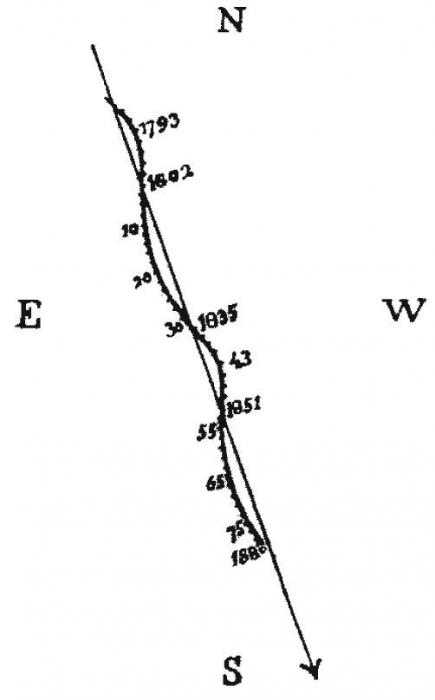
Etalonner la figure de l'appliquette, en tenant compte du fait que les portions de cercle centrés sur Sirius A sont espacés de 1 seconde d'angle, et définir le rapport d'unité permettant de lire directement des secondes d'angle sur la figure.
Estimer le demi-grand axe de l'orbite relative et la période.
La parallaxe du système vaut 0.379". En déduire la somme des masses des deux composantes (en unités de masse solaire).
Le mouvement de Sirius A par rapport au barycentre présente une demi-amplitude de 2.35" au cours d'une orbite (corrigée de la projection du plan orbital sur le plan du ciel). Comparer cette amplitude au mouvement relatif des 2 composantes, et en déduire la masse de chaque composante.
pages_visuelles/intro-binaires-visuelles-sexercer.html
On appelle 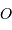 le centre de l'ellipse observée et A l'intersection de la demi-droite [0E) avec l'ellipse. Comme l'excentricité
le centre de l'ellipse observée et A l'intersection de la demi-droite [0E) avec l'ellipse. Comme l'excentricité 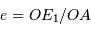 est invariante par projection, le fait que l'étoile primaire soit au foyer de l'orbite projetée montre que le grand axe de l'orbite projetée correspond à la projection du grand axe, ce qui ne peut avoir lieu que si
est invariante par projection, le fait que l'étoile primaire soit au foyer de l'orbite projetée montre que le grand axe de l'orbite projetée correspond à la projection du grand axe, ce qui ne peut avoir lieu que si 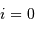 ...
...
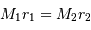 et
et 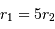 implique un rapport de masse
implique un rapport de masse 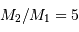
La troisième loi de Kepler, en unités, UA, année, masse solaire, s'exprime :
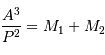
La parallaxe étant de 0.1", le système double est situé à 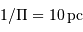 de nous et qu'une unité astronomique y est vue sous un angle de 0,1".
de nous et qu'une unité astronomique y est vue sous un angle de 0,1".
Le demi-grand axe apparent est égal à 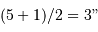 ; le demi-grand axe est donc de 30 UA.
; le demi-grand axe est donc de 30 UA.
On applique la troisième loi de Kepler pour calculer la somme des masses :
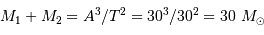 .
.
et on obtient 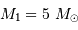 et
et 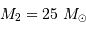
pages_visuelles/masse-sirius-sexercer.html
Activité soit l'outil 'ligne', soit l'outil 'cercle'.
Faire une règle de trois et définir le rapport d'unité.
Avec l'outil 'cercle' centré sur Sirius A, 10" correspondent à 350 unités. On définit le rapport d'unité : 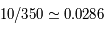
Pour le demi-grand axe : repérer les projections des péri- et apoastre.
Pour la période : s'appuyer sur les valeurs au voisinage de l'apoastre.
D'après la figure, on déduit la période 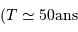 et le demi-grand axe de l'orbite relative
et le demi-grand axe de l'orbite relative 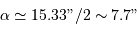
Traduire la parallaxe en distance.
De la valeur angulaire du demi-grand axe et de la distance, déterminer le demi-grand axe en UA.
Utiliser la 3ème loi de Kepler
Si 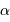 est le demi-grand axe mesuré en secondes d'arc et
est le demi-grand axe mesuré en secondes d'arc et 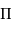 la parallaxe, le demi-grand axe linéaire
la parallaxe, le demi-grand axe linéaire 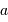 , mesuré en UA est alors égal à
, mesuré en UA est alors égal à 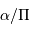 , soit
, soit 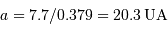 .
.
D'après la troisième loi de Kepler, on a par ailleurs :
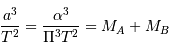
où 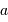 est exprimé en UA,
est exprimé en UA, 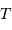 en années, et
en années, et 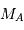 et
et 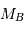 en masse solaire. Ce qui donne :
en masse solaire. Ce qui donne :
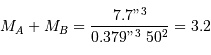
Définir le barycentre.
La demi-amplitude est à comparer au demi-grand axe.
La définition du barycentre G donne :
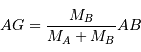
On peut ainsi comparer la demi-amplitude de AG au demi-grand axe, pour obtenir le rapport 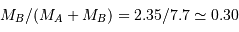 .
.
On en déduit les masses respectives : 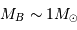 et
et 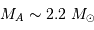 .
.