Astrolabe

Auteur: Marc Fouchard

astrolabe

Astrolabe du XVI siècle.

Crédit : David Monniaux, licence : CC BY-SA 3.0

Auteur: Marc Fouchard

L'astrolabe est un outil astronomique permettant de représenter la partie du ciel observée en fonction de la date et de l'heure pour un lieu donné. Il permet ensuite de faire différentes mesures comme la détermination des heures de lever et de coucher d'un astre. Les applications de l'astrolabe sont pourtant très nombreuses. Pour avoir plus de détails, on pourra aller voir l'astrolabe.

La construction d'un astrolabe repose sur la projection stéréographique. Le but de cet exercice est d'étudier les propriétés principales de cette projection et d'en déduire l'image de points et de cercles caractéristiques de la sphère céleste.

Ce sont ces constructions qui ont permis de construire l'animation suivante.

astrolabe

Astrolabe.

Crédit : Astrophysique sur Mesure / Damien Guillaume / Marc Fouchard

sphère céleste

Sur une sphère céleste un point est repéré par une longitude et une latitude. La latitude correspond à un angle entre $[-\pi/2,\pi/2]$ donnant la hauteur au dessus d'un grand cercle de référence et en choisissant un côté positif (comme sur Terre, la latitude d'un lieu correspond à une hauteur au-dessus de l'équateur, comptée positivement dans l'hémisphère nord). Ce cercle de référence permet de définir l'axe des pôles et les pôles. La longitude correspond à l'angle, compris dans l'intervalle $[0,2\pi]$ , entre un méridien de référence et le méridien passant par le point considéré. Cet angle est mesuré sur le cercle de référence en choisissant un sens positif. Sur la Terre les longitudes sont mesurées à partir du méridien passant par Greenwich en prenant comme sens positif la direction de l'Ouest (ce qui correspond au sens des aiguilles d'une montre lorsqu'on regarde du pôle nord).

Dans notre cas, la sphère céleste 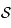$\mathcal{S}$ est une sphère de rayon unité (arbitraire), centrée sur l'observateur. Sur cette sphère on projette l'équateur terrestre, ce qui nous donne un grand cercle , appelé équateur céleste, le pôle nord se projette au point 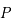et le pôle sud au point 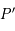, appelés respectivement pôle céleste nord et pôle céleste sud.

En astronomie différents ensembles de longitude et de latitude sont utilisés :

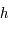les coordonnées locales : le grand cercle de référence correspond à la projection de l'horizon sur la sphère céleste. Les pôles sont donc la direction de la verticale du lieu appelé zénith et la direction opposée appelée Nadir. Ainsi, la latitude correspond à une hauteur sur l'horizon céleste, notée et positive au dessus de l'horizon, et une longitude mesurée sur l'horizon céleste, appelée azimut et notée 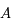, en prenant comme méridien d'origine celui passant par le pôle céleste sud et comme sens positif vers l'ouest.
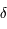Les coordonnées horaires : définies par rapport à l'équateur céleste, avec une latitude, appelée déclinaison et notée $\delta$ , positive vers le pôle céleste nord, et une longitude appelée angle horaire et noté 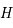, avec comme méridien d'origine le méridien passant par le zénith et comme sens positif vers l'ouest.
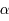Les coordonnées équatoriales :même latitude que le précédent mais la longitude, appelée ascension droite et notée $\alpha$ , est mesurée par rapport au méridien d'origine qui contient la position du Soleil au moment de l'équinoxe de printemps et le sens positif est le sens trigonométrique (vue du pôle nord). Cette position est appelé le point vernal et ce sens positif correspond au sens du mouvement annuel du Soleil.

La figure ci-dessous montre la correspondance entre ces différents systèmes de coordonnées. On remarquera aussi sur la figure le lien entre la position du zénith et la latitude terrestre du lieu.

sphère céleste

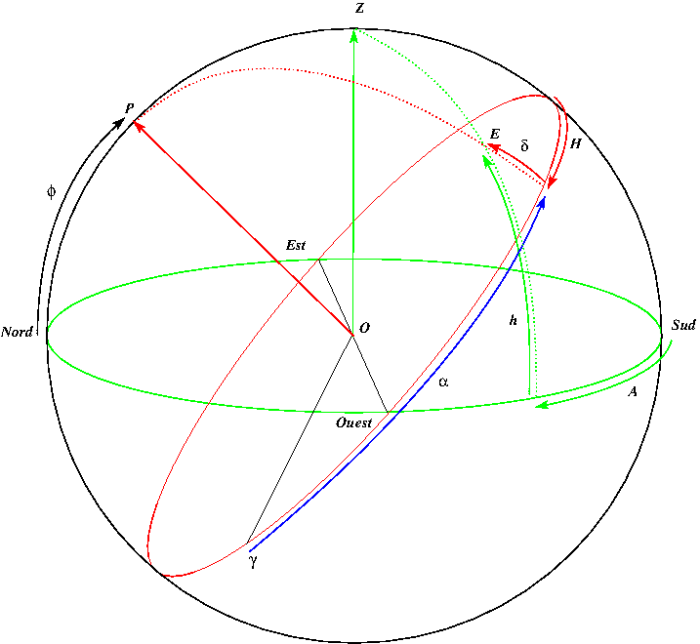
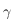Les coordonnées utilisées en astronomie. Le grand cercle vert correspond à l'horizon céleste et le rouge à l'équateur céleste. La hauteur du pôle céleste nord sur l'horizon correspond à la latitude du lieu. Le point $\gamma$ correspond à la direction du point vernal.

Crédit : Astrophysique sur Mesure / Marc Fouchard

En un lieu de latitude 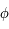$\phi$ on a alors les équations suivantes permettant de passer d'un ensemble de coordonnées à l'autre:

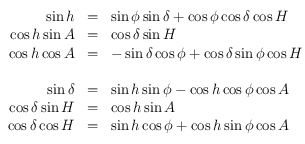
$\begin{array}{rcl}\sin h&=& \sin \phi \sin \delta + \cos \phi \cos \delta \cos H \\ \cos h \sin A &=& \cos \delta \sin H \\ \cos h \cos A &=& -\sin \delta \cos \phi + \cos \delta \sin \phi \cos H \\ && \\ \sin \delta &=& \sin h \sin \phi - \cos h \cos \phi \cos A \\ \cos \delta \sin H &=& \cos h \sin A \\ \cos \delta \cos H &=& \sin h \cos \phi + \cos h \sin \phi \cos A \end{array}$

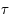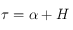Le lien entre l'ascension droite et l'angle horaire se fait en utilisant l'angle horaire du point vernal appelé temps sidéral, que l'on notera $\tau$ . On a la relation : $\tau=\alpha+H$ .