Apprendre

Prérequis

Objectifs

Illustrer le problème à N-corps dans un cas particulier : 3 corps, dont 1 de masse négligeable devant les 2 autres. Dans ce cas, on ne considère que le champ gravitationnel des 2 corps massifs.

3 corps, mais 1 de masse nulle

Le problème à 3-corps est insoluble analytiquement dans le cas général. L'astronome mathématicien Joseph-Louis Lagrange en a proposé une solution dans un cas particulier, où l'un des corps est de masse négligeable devant les 2 autres, et subit leurs champs gravitationnels.

Le potentiel gravitationnel

Les 2 corps massifs sont supposés en orbite circulaire ; on note 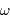$\omega$ la vitesse angulaire de rotation. Le potentiel gravitationnel créé par ces 2 corps est étudié dans le référentiel tournant avec les 2 corps, supposés en orbite circulaire. Les notations sont définis ci-joint.

Le corps de masse négligeable subit le potentiel :

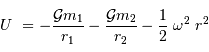
$U \ = - { {\cal G} m_1\over r_1} - { {\cal G} m_2\over r_2} - {1\over 2}\ \omega^2 \ r^2$

avec 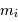m_i les masses respectives des 2 corps massifs, 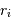r_i les distances du système aux 2 corps, 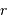la distance à leur barycentre, et 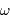$\omega$ la vitesse angulaire de rotation des 2 corps. Le dernier terme est introduit par le référentiel tournant.

En posant 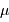$\mu$ le rapport des masses 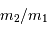m_2/m_1 , et en notant 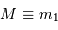$M\equiv m_1$ la plus forte des masses, on obtient :

$U \ = - { {\cal G} M}\ \left[ {1\over r_1} + {\mu\over r_2} + {1\over 2}\ {(1+\mu) r^2\over a^3} \right]$

en ayant introduit la 3e loi de Kepler pour les 2 corps massifs : 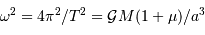$\omega^2= 4\pi^2 / T^2 = {\cal G} M (1+\mu) /a^3$ .

Les points de Lagrange

Le gradient de potentiel s'annule en des points particuliers : les points de Lagrange. Leur étude peut être menée analytiquement, mais l'on se contente ici de constater les résultats.

Ces points se situent dans le plan orbital des 2 corps. Les points L1, L2 et L3 sont alignés avec les 2 corps, et L4 et L5 forment avec eux 2 triangles équilatéraux.

Equilibre aux points de Lagrange

Il faut noter que les positions d'équilibre trouvées ne sont pas statiquement stables : ils correspondent en effet à des maximum de potentiel, ou des selles. C'est dynamiquement, avec l'appoint de la force de Coriolis (le référentiel est tournant !) que les points L4 et L5 deviennent stables... et sont occupés par des satellites naturels ou artificiels.