

Ex: Perturbations linéaires |
Difficulté : ☆☆ Temps : 1 h
Les équations fondamentales gouvernant le mouvement d'un fluide sont:
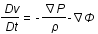
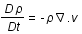
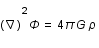 .
.
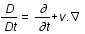 est la dérivée convective (variation totale dûe à la variation temporelle,
est la dérivée convective (variation totale dûe à la variation temporelle, 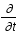 , et spatiale,
, et spatiale, 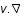 , du fluide) , v la vitesse du fluide, P sa pression,
, du fluide) , v la vitesse du fluide, P sa pression, 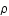 sa densité, G la constante de gravitation et
sa densité, G la constante de gravitation et 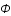 le potentiel gravitationnel.
On souhaite tout d'abord linéariser les équations autour d'un fond homogène,
le potentiel gravitationnel.
On souhaite tout d'abord linéariser les équations autour d'un fond homogène, 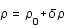 ,
, 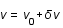 ,
, 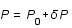 et
et 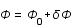 .
.
Soustraire à ces équations les équations à l'ordre 0 (c.à.d. les équations non perturbées où les 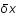 sont nuls) et les exprimer en fonction du contraste de densité
sont nuls) et les exprimer en fonction du contraste de densité 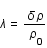
La dérivée convective des quantités perturbées est donc 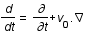 . Ces équations sont écrites en coordonnées eulériennes x(t) (système de coordonnées fixes). On se propose maintenant de les écrire en coordonnées comobiles, r(t), système de coordonnées qui évolue et se dilate avec l'expansion de l'universafin de s'en affranchir. Le passage de l'une à l'autre se fait par:
. Ces équations sont écrites en coordonnées eulériennes x(t) (système de coordonnées fixes). On se propose maintenant de les écrire en coordonnées comobiles, r(t), système de coordonnées qui évolue et se dilate avec l'expansion de l'universafin de s'en affranchir. Le passage de l'une à l'autre se fait par:
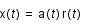 et
et 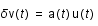 où
où 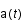 est le facteur d'échelle caractérisant l'expansion et
est le facteur d'échelle caractérisant l'expansion et 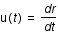 est la vitesse particulière du fluide.
On peut montrer que
est la vitesse particulière du fluide.
On peut montrer que 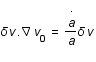 . Réecrire les équations d'Euler et de conservation en fonction de a et u(t).
. Réecrire les équations d'Euler et de conservation en fonction de a et u(t).
La vitesse du son 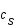 est par définition
est par définition 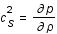 .
Dériver l'équation de conservation afin de déterminer l'équation différentielle du deuxième ordre régissant l'évolution de
.
Dériver l'équation de conservation afin de déterminer l'équation différentielle du deuxième ordre régissant l'évolution de 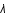 .
.