Ex: Potentiel gravitationnel terrestre

Auteurs: Jérôme Thiébaut, Arnaud Beck

Auteur: Arnaud Beck

Potentiel gravitationnel terrestre

Difficulté : ☆ Temps : 1h

Introduction

Dans le repère du centre de gravité de la Terre et en supposant la Terre à symétrie de révolution autour de son axe, on peut montrer qu'une bonne approximation du potentiel gravitationnel est donné par

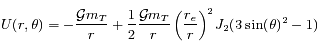
$U(r,\theta)=-\frac{\mathcal{G}m_T}{r}+\frac{1}{2}\frac{\mathcal{G}m_T}{r}\left(\frac{r_e}{r}\right)^2J_2(3\sin (\theta)^2-1)$

où 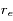r_e est le rayon équatorial de la Terre, 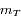m_T sa masse, 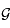$\mathcal{G}$ la constante de gravitation, 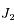J_2 un coefficient de correction sans dimension, 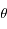$\theta$ la latitude et 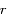la distance au centre.

Question 1)

Sachant que le champ de gravitation est donné par le gradient du potentiel 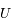, donner les composantes radiale et tangentielle de ce champ.

Aide Solution

Question 2)

En symétrie parfaitement sphérique, le champ gravitationnel de la Terre est non nul en tout point de l'espace. Il est intéressant de noter que ce n'est pas le cas si l'on prend en compte l'aplatissement de la Terre. Déterminer les points en lesquels le champ gravitationnel s'annule. D'un de point de vue mathématique, que sont ces points pour la fonction ?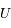

Aide Solution

Question 3)

Voici une représentation de 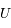en niveau de gris. Le cercle blanc centrale est une zone où le potentiel diverge et n'est pas évalué. Il ne faut donc pas en tenir compte. En faisant des coupes sur cette image, déterminer la variation de 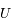dans les directions radiale et tangentielle au niveau des points critiques. En déduire si ces points sont des minima, des maxima ou des points selles.

Représentation de

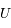en niveau de gris. L'axe de la terre 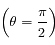$\left( \theta=\frac{\pi}{2} \right)$ est vertical. Les zones blanches correspondent à un potentiel positif et les zones sombres à un potentiel négatifs. Le cercle blanc du milieu est une zone ou le potentiel diverge (car

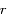est trop petit) et n'est pas évalué. Faites des coupes avec la souris et cliquer sur graphe pour afficher l'évolution du potentiel le long de la coupe.

Crédit : Arnaud Beck

Solution