Equation aux dimensions

Auteur: Stéphane Erard

On peut toujours multiplier ou diviser des grandeurs quelconques entre elles, mais on ne peut additionner que des grandeurs physiques de même dimension — l'inverse reviendrait littéralement à additionner les torchons et les serviettes.

Les équations ou formules doivent donc être homogènes : chaque membre (et chaque terme) d'une équation doit avoir la même dimension physique. La vérification de l'homogénéité d'une formule ou d'un résultat de calcul doit être un réflexe en physique : c'est un moyen efficace pour éliminer les erreurs de calcul, et éviter les non-sens.

Exemple

Le principe fondamental de la dynamique donne la dimension physique de la force :

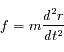
$f = m \frac{d^2r}{dt^2}$

L'équation aux dimensions est :

$[F]= MLT^{-2}$

et l'unité SI de la force est le 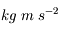$kg\;m\;s^{-2}$ (couramment appelée Newton).

Les constantes qui apparaissent dans les lois physiques ont également une dimension. On peut dériver celle-ci en posant l'équation aux dimensions. La valeur numérique dépend encore une fois du système d'unités utilisé.

Exemple

L'attraction universelle (loi de Newton) s'écrit :

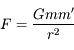
$F= \frac{Gmm'}{r^2}$

où G est la constante de gravitation. La dimension de G est donc

$[G]= [F]L^2M^{-2}=L^3T^{-2}M^{-1}$

La valeur numérique doit se mesurer expérimentalement, et dépend du système d'unités adopté.

Les fonctions mathématiques n'acceptent que des arguments sans dimension, ou dédimensionalisés. En pratique, ce sont des nombres purs ou des rapports de quantités de même grandeur.

Exemple

L'équation de Boltzmann donne la population d'un niveau d'énergie atomique ou moléculaire en fonction de la température :

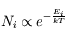
$N_i \propto e^{- \frac{E_i}{kT}}$

La quantité kT est donc homogène à une énergie.

On peut en déduire la dimension physique de la constante de Boltzmann k :

La dimension d'une énergie est donnée par exemple par 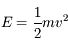$E = \frac{1}{2}m v^2$

On a donc 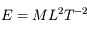$E = ML^2T^{-2}$ (l'unité SI est le 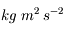$kg\;m^2\;s^{-2}$ , couramment appelée Joule)
La dimension de la constante de Boltzmann est donc $[k] = ML^2T^{-2}K^{-1}$ . La valeur de k est donnée en J/K en SI.

Les équations aux dimensions permettent également de dériver les ordres de grandeur de phénomènes physiques, éventuellement en utilisant des modèles dérivés d'hypothèses simples.

Exemple

L'équation barométrique dérive d'un modèle basique d'atmosphère isotherme. Elle donne la pression P en fonction de l'altitude z sous ces hypothèses très simplifiées :

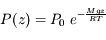
$P(z) = P_0\; e^{-\frac{Mgz}{RT}}$

où 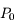P_0 est la pression au sol, M la masse molaire moyenne, R la constante des gaz parfaits, g l'accélération de la pesanteur, et T la température (supposée constante) de l'atmosphère.

La quantité h = RT/Mg est donc homogène à une distance — c'est l'altitude à laquelle la pression est réduite d'un facteur 2,7 dans ce modèle. Elle est appelée échelle de hauteur, et donne une estimation de l'épaisseur de la basse atmosphère des planètes.

On peut l'évaluer dans la troposphère terrestre :

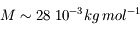$M \sim 28 \ 10^{-3} kg \, mol^{-1}$ (masse molaire de l'azote, principal constituant)

T ~ 280 K (température au sol)

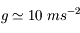
$g \simeq 10\; ms^{-2}$

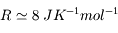
$R \simeq 8\; JK^{-1}mol^{-1}$

Ce qui donne pour l'échelle de hauteur h ~ 8 km.

De façon similaire, chaque grandeur possède une dimension tensorielle : scalaire, vecteur, ou tenseur d'ordre supérieur. La dimension tensorielle se préserve de la même façon que la dimension physique (chaque terme d'une équation doit avoir la même dimension tensorielle).

Exemple

Le principe fondamental de la dynamique peut s'écrire de manière vectorielle, et donne la direction de la force :

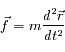
$\vec{f} = m \frac{d^2\vec{r}}{dt^2}$

On peut aussi l'écrire de manière scalaire en utilisant les normes :

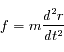
$f = m \frac{d^2r}{dt^2}$

Les tenseurs d'ordre 2 sont utilisés pour décrire des quantités qui en chaque endroit dépendent aussi de la direction. Des exemples de tenseurs d'ordre 2 sont donnés par le tenseur métrique de la relativité générale, ou par les tenseurs de contrainte et de déformation en mécanique des milieux continus.