Ex: analyse dimensionnelle

Les paramètres physiques qui interviennent sont : la masse oscillante m, la longueur l du pendule, la période d'oscillation p, l'angle initial 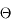et la pesanteur g (on néglige au premier ordre les autres paramètres tels que le frottement ou la masse du fil, qui décrivent des écarts au problème idéal).

Au total, on a 5 grandeurs et 3 dimensions physiques indépendantes (longueur, temps et masse). La relation cherchée peut donc s'écrire comme une relation entre deux nombres sans dimension construits avec ces 5 grandeurs.

Le premier nombre est évidemment l'angle initial 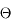, sans dimension.

Le second nombre est de la forme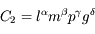

L'équation aux dimensions est , donc 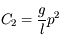est sans dimension.

Le relation cherchée est de la forme 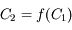, soit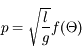

Le calcul à partir de l'équation du mouvement donne 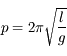, et l'expérience confirme que la période ne dépend pas de l'angle initial si celui-ci est petit. On a montré sans le moindre effort la forme générale de la période (à une constante près) et le fait qu'elle ne dépend pas de la masse du pendule.