Séries du problème des 2-corps

Auteurs: Alain Vienne, S. Renner

Auteur: Alain Vienne

Souvent, lorsque l'on considère le problème des 2 corps et quand l'excentricité de l'orbite est petite, on a besoin de l'approximation suivante:

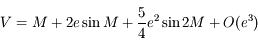
$V=M+2e \sin M + \frac{5}{4}e^2 \sin 2M +O (e^3)$

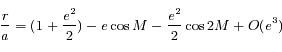
$\frac{r}{a}=(1+\frac{e^2}{2})-e\cos M - \frac{e^2}{2} \cos 2M +O (e^3)$

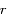et 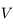sont les coordonnées polaires du corps, 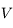étant compté à partir du péricentre (anomalie vraie). 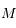est le temps ou plus précisément c'est l'anomalie moyenne 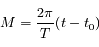$M=\frac{2\pi}{T} (t-t_0)$ avec 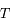la période, 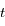le temps et 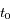t_0 l'instant de passage au péricentre. 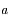et sont respectivement le demi-grand axe et l'excentricité de l'orbite.

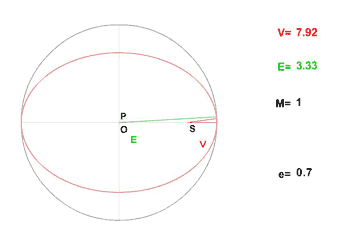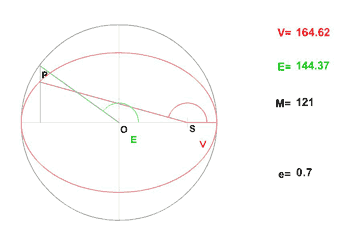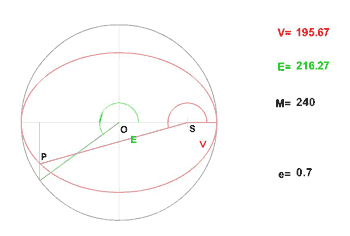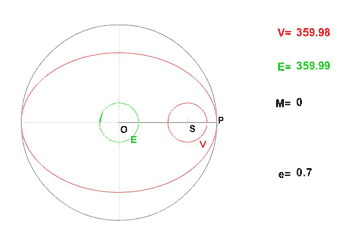
Dans l'exercice qui est proposé ci-après, on utilisera en plus des anomalies moyennes et vraies, l'anomalie excentrique. L'animation qui est donnée ici visualise leur évolution dans le cas d'une excentricité de 0,7.

Evolution des 3 anomalies (respectivement vraie, excentrique et moyenne)

Crédit : Astrophysique sur Mesure / Bessou

Si l'existence des développements ci-dessus est admise, l'astronome s'autrorise alors une démarche pragmatique pour les obtenir. Sa démarche n'a pas la rigueur du mathématicien. Dans le cas présenté ici, elle n'a pas non plus une grande efficacité si on souhaite "pousser" le développement plus loin en ordre.Elle a le seul avantage de pouvoir "se tirer d'affaire" dans le cas qui le préoccupe.

Dans l'exercice qui est proposé, on utilisera au besoin le développement de Taylor, l'intégration d'un développement, la substitution de développements.

Exercices reliés

Pour la recherche de la solution du problème des 2-corps, on peut voir cet exercice. Il y aussi celui qui utilse le théorème de Lagrange. D'autres exercices sur le problème de 2 corps existent sur ce site. On en trouvera, entre autres, sur l'équation de Kepler et son inversion, sur les solutions géométriques du problème de 2 corps, sur le problème de 2 corps perturbé et sur l'excentricité limite dans les développements du problème de 2 corps.