Séries du problème des 2-corps (Lagrange)

Auteurs: Alain Vienne, S. Renner

Auteur: S. Renner

Date de création: 10 avril 2013

Dans le problème des 2 corps, lorsque l'excentricité 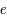de l'orbite est petite, on peut écrire :

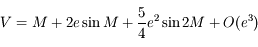$V=M+2e \sin M + \frac{5}{4}e^2 \sin 2M +O (e^3)$ ,

où 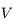est l'angle entre la direction du péricentre et la position du corps sur son orbite (anomalie vraie), 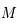est le temps ou plus précisément l'anomalie moyenne 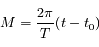$M=\frac{2\pi}{T} (t-t_0)$ , avec 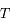la période, 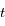le temps et 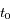t_0 l'instant de passage au péricentre.

L'animation donnée ci-après montre l'évolution des anomalies vraie et moyenne (et excentrique) dans le cas d'une excentricité 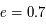e=0.7 .

Evolution des 3 anomalies (respectivement vraie, excentrique et moyenne)

Crédit : Astrophysique sur Mesure / Bessou

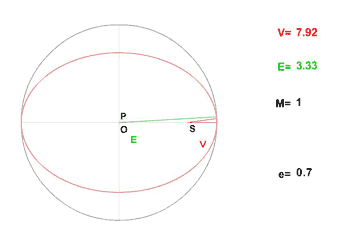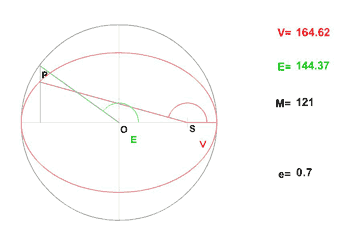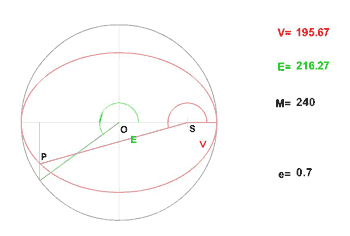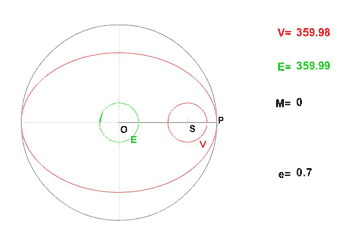
Dans l'exercice proposé, on établit le développement ci-dessus à l'aide du théorème d'inversion de Lagrange.