Auteur: Alain Vienne
Souvent, lorsque l'on considère le problème des 2 corps et quand l'excentricité  de l'orbite est petite, on a besoin de l'approximation suivante:
de l'orbite est petite, on a besoin de l'approximation suivante:
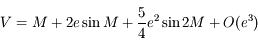
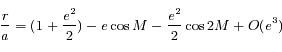
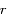 et
et 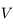 sont les coordonnées polaires du corps,
sont les coordonnées polaires du corps, 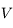 étant compté à partir du péricentre (anomalie vraie).
étant compté à partir du péricentre (anomalie vraie). 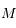 est le temps ou plus précisément c'est l'anomalie moyenne
est le temps ou plus précisément c'est l'anomalie moyenne 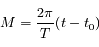 avec
avec 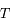 la période,
la période, 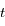 le temps et
le temps et 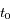 l'instant de passage au péricentre.
l'instant de passage au péricentre. 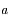 et
et  sont respectivement le demi-grand axe et l'excentricité de l'orbite.
sont respectivement le demi-grand axe et l'excentricité de l'orbite.
Dans l'exercice qui est proposé ci-après, on utilisera en plus des anomalies moyennes et vraies, l'anomalie excentrique.
L'animation qui est donnée ici visualise leur évolution dans le cas d'une excentricité de 0,7.
Evolution des 3 anomalies (respectivement vraie, excentrique et moyenne)
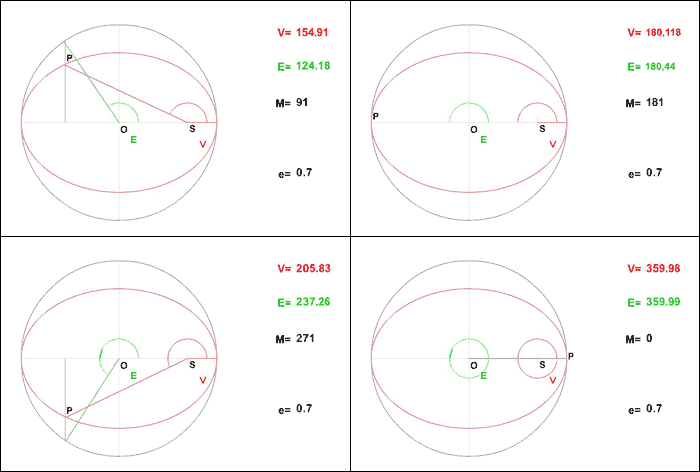
Si l'existence des développements ci-dessus est admise, l'astronome s'autrorise alors une démarche pragmatique pour les obtenir. Sa démarche n'a pas la rigueur du mathématicien. Dans le cas présenté ici, elle n'a pas non plus une grande efficacité si on souhaite "pousser" le développement plus loin en ordre.Elle a le seul avantage de pouvoir "se tirer d'affaire" dans le cas qui le préoccupe.
Dans l'exercice qui est proposé, on utilisera au besoin le développement de Taylor, l'intégration d'un développement, la substitution de développements.
Auteur: Alain Vienne
 Séries du problème des 2-corps
Séries du problème des 2-corps
Difficulté : ☆☆
Temps : 1h
 Introduction
Introduction
Quand on intègre le problème des 2-corps, la loi des aires permet d'écrire:
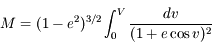
Question 1)
On utilisant cette relation et en négligeant les termes d'ordre supérieur ou égal à 3 en excentricité, montrer que l'on a:
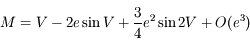
Développer d'abord 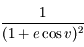 et intégrer le développement obtenu. Mutiplier enfin par celui de
et intégrer le développement obtenu. Mutiplier enfin par celui de 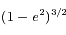 . Dans ces calculs, on prend soin de se limiter à l'ordre 2.
. Dans ces calculs, on prend soin de se limiter à l'ordre 2.
Question 3)
A partir du développement obtenu à la première question, déduire celui qui donne 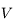 en fonction de
en fonction de 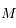 (limité à l'ordre 2 en
(limité à l'ordre 2 en  ).
).
Faire d'abord l'ordre 0 puis l'ordre 1 et enfin l'ordre 2.
A l'ordre 0: 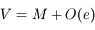
A l'ordre 1, il suffit d'avoir 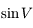 à l'ordre 0 (obtenu précédemment).
à l'ordre 0 (obtenu précédemment).
A l'ordre 2, il suffit d'avoir 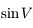 à l'ordre 1 et
à l'ordre 1 et 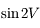 à l'ordre 0 (obtenus précédemment).
à l'ordre 0 (obtenus précédemment).
L'ordre 1 pour 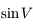 est obtenu de la manière suivante:
est obtenu de la manière suivante: 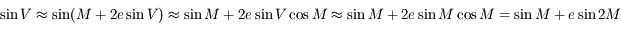 . Attention à la discussion sur l'ordre à chaque étape du calcul.
. Attention à la discussion sur l'ordre à chaque étape du calcul.
 Remarque
Remarque
Dans cette dernière question, le calcul est fait "en crabe", il faut donc veiller à la discussion sur l'ordre en excentricité. Plus généralement, tous ces calculs supposent l'existence des développements recherchés. Cette supposition et l'unicité ont permis d'éviter de se soucier des conditions d'application des théorèmes utilisés.
Auteur: S. Renner
Date de création: 10 avril 2013
Dans le problème des 2 corps, lorsque l'excentricité 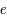 de l'orbite est petite, on peut écrire :
de l'orbite est petite, on peut écrire :
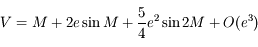 ,
,
où 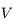 est l'angle entre la direction du péricentre et la position du corps sur son orbite (anomalie vraie),
est l'angle entre la direction du péricentre et la position du corps sur son orbite (anomalie vraie), 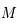 est le temps ou plus précisément l'anomalie moyenne
est le temps ou plus précisément l'anomalie moyenne 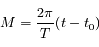 , avec
, avec 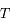 la période,
la période, 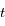 le temps et
le temps et 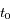 l'instant de passage au péricentre.
l'instant de passage au péricentre.
L'animation donnée ci-après montre l'évolution des anomalies vraie et moyenne (et excentrique) dans le cas d'une excentricité 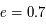 .
.
Evolution des 3 anomalies (respectivement vraie, excentrique et moyenne)

Dans l'exercice proposé, on établit le développement ci-dessus à l'aide du théorème d'inversion de Lagrange.
Auteur: S. Renner
 Séries du problème des 2-corps (Lagrange)
Séries du problème des 2-corps (Lagrange)
Difficulté : ☆☆
Temps : 1h
Question 1)
On utilisant cette relation et en négligeant les termes d'ordre supérieur ou égal à 3 en excentricité, montrer que l'on a:
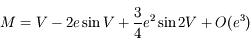
Développer d'abord 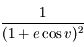 et intégrer le développement obtenu. Mutiplier enfin par celui de
et intégrer le développement obtenu. Mutiplier enfin par celui de 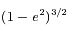 . Dans ces calculs, on prend soin de se limiter à l'ordre 2.
. Dans ces calculs, on prend soin de se limiter à l'ordre 2.
Auteur: S. Renner
Date de création: 3 février 2010
Souvent en dynamique du système solaire, l'excentricité est très faible, et il est donc utile de considérer des approximations au premier ordre en excentricité, en particulier pour des systèmes vus dans des repères tournants. Cette approche est par exemple intéressante pour décrire la dynamique des anneaux planétaires, ou les effets de l'aplatissement d'une planète sur les orbites de satellites.
On propose ici un exercice qui porte sur la description du mouvement keplerien par des épicycles : le mouvement elliptique d'une particule P autour d'un foyer F est vu dans un repère centré sur un point G (le centre guide) en orbite circulaire uniforme autour de F (de rayon a égal au demi-grand axe de la particule, et de vitesse angulaire égale au moyen mouvement 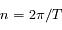 , où
, où 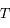 est la période orbitale de P).
est la période orbitale de P).
L'exercice est largement inspiré du livre Solar System Dynamics (C.D. Murray & S.F. Dermott, 1999).
Auteur: S. Renner
 Description épicyclique du mouvement keplerien
Description épicyclique du mouvement keplerien
Difficulté : ☆☆
Temps : 2h
Question 2)
A partir de la loi des aires, montrer que: 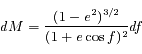 .
.
Question 3)
Ainsi en intégrant on obtient: 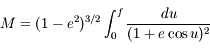 . Montrer à l'aide de cette relation que
. Montrer à l'aide de cette relation que 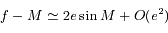 .
.
Auteur: S. Renner et A. Vienne
Date de création: 3 mars 2010
Nous allons définir la notion de sphère d'influence en s'intéressant au problème à trois corps Soleil + Jupiter + satellite, de masses respectives 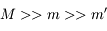 (qui constitue ce que l'on appelle un problème de Kepler perturbé).
(qui constitue ce que l'on appelle un problème de Kepler perturbé).
Auteurs: S. Renner, A. Vienne
 Sphère d'influence
Sphère d'influence
Difficulté : ☆☆
Temps : 3h
Question 1)
Ecrire les équations du mouvement héliocentrique de 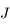 (c'est-à-dire de
(c'est-à-dire de 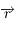 ).
).
Question 2)
Quelle est la nature du mouvement de 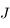 si la quantité
si la quantité 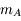 est négligeable?
est négligeable?
Question 4)
Montrer que l'équation du mouvement jovicentique de 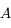 (c'est-à-dire de
(c'est-à-dire de 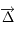 ) est
) est 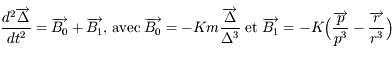 .
.
Question 5)
Dans la suite, on cherche à étudier la surface 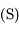 définie par
définie par 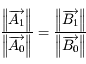 . On va voir notamment qu'elle a presque la forme d'une sphère,
appelée sphère d'influence de Jupiter. Justifier cette appellation en expliquant ce qui se passe pour le mouvement de
. On va voir notamment qu'elle a presque la forme d'une sphère,
appelée sphère d'influence de Jupiter. Justifier cette appellation en expliquant ce qui se passe pour le mouvement de 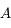 lorsque celui-ci est respectivement très à
l'intérieur ou très à l'extérieur de cette sphère.
lorsque celui-ci est respectivement très à
l'intérieur ou très à l'extérieur de cette sphère.
Question 6)
On pose 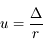 et
et 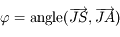 . Montrer que l'on a
. Montrer que l'on a 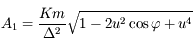 .
.
Question 7)
Montrer que l'on a 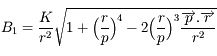 .
.
Question 9)
En déduire que l'équation de la surface 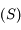 peut s'écrire
peut s'écrire 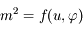 , et donner l'expression de
, et donner l'expression de 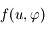 .
.
Question 11)
Calculer le rayon de la sphère d'influence de Jupiter sachant que 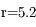 UA.
UA.
 de l'orbite est petite, on a besoin de l'approximation suivante:
de l'orbite est petite, on a besoin de l'approximation suivante:
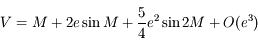
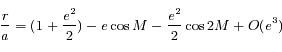
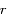 et
et 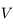 sont les coordonnées polaires du corps,
sont les coordonnées polaires du corps, 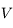 étant compté à partir du péricentre (anomalie vraie).
étant compté à partir du péricentre (anomalie vraie). 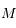 est le temps ou plus précisément c'est l'anomalie moyenne
est le temps ou plus précisément c'est l'anomalie moyenne 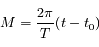 avec
avec 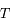 la période,
la période, 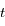 le temps et
le temps et 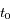 l'instant de passage au péricentre.
l'instant de passage au péricentre. 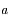 et
et  sont respectivement le demi-grand axe et l'excentricité de l'orbite.
sont respectivement le demi-grand axe et l'excentricité de l'orbite.

 Exercices reliés
Exercices reliés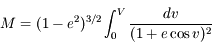
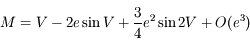
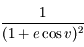 et intégrer le développement obtenu. Mutiplier enfin par celui de
et intégrer le développement obtenu. Mutiplier enfin par celui de 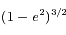 . Dans ces calculs, on prend soin de se limiter à l'ordre 2.
. Dans ces calculs, on prend soin de se limiter à l'ordre 2.
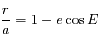 et
et 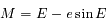 (
(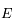 est l'
est l' en puissance de
en puissance de  et en fonction de
et en fonction de 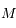 (limité à l'ordre 2)
(limité à l'ordre 2)
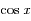 en
en 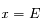 au voisinage de
au voisinage de 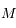 , c'est-à-dire, écrire:
, c'est-à-dire, écrire: 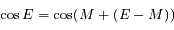 .
.
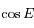 n'est utile que jusque l'ordre 1 !
n'est utile que jusque l'ordre 1 !
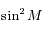 .
.
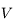 en fonction de
en fonction de 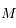 (limité à l'ordre 2 en
(limité à l'ordre 2 en  ).
).
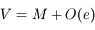
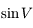 à l'ordre 0 (obtenu précédemment).
à l'ordre 0 (obtenu précédemment).
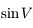 à l'ordre 1 et
à l'ordre 1 et 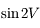 à l'ordre 0 (obtenus précédemment).
à l'ordre 0 (obtenus précédemment).
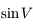 est obtenu de la manière suivante:
est obtenu de la manière suivante: 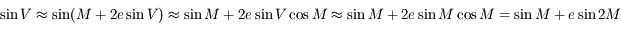 . Attention à la discussion sur l'ordre à chaque étape du calcul.
. Attention à la discussion sur l'ordre à chaque étape du calcul.
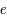 de l'orbite est petite, on peut écrire :
de l'orbite est petite, on peut écrire :
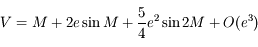 ,
,
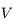 est l'angle entre la direction du péricentre et la position du corps sur son orbite (
est l'angle entre la direction du péricentre et la position du corps sur son orbite (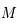 est le temps ou plus précisément l'anomalie moyenne
est le temps ou plus précisément l'anomalie moyenne 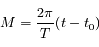 , avec
, avec 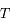 la période,
la période, 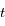 le temps et
le temps et 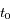 l'instant de passage au péricentre.
l'instant de passage au péricentre.
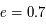 .
.
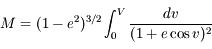
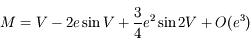
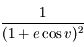 et intégrer le développement obtenu. Mutiplier enfin par celui de
et intégrer le développement obtenu. Mutiplier enfin par celui de 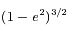 . Dans ces calculs, on prend soin de se limiter à l'ordre 2.
. Dans ces calculs, on prend soin de se limiter à l'ordre 2.
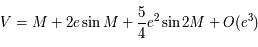 .
.
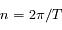 , où
, où 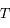 est la période orbitale de P).
est la période orbitale de P).
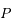 sur une ellipse de foyer
sur une ellipse de foyer 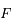 et de demi-grand axe
et de demi-grand axe 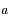 . On note
. On note 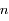 le moyen mouvement de la particule, et
le moyen mouvement de la particule, et 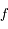 son
son 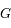 un point fictif tournant autour du foyer
un point fictif tournant autour du foyer 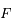 sur une orbite circulaire de rayon
sur une orbite circulaire de rayon 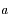 égal au demi-grand axe de
égal au demi-grand axe de 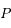 , avec une vitesse angulaire égale au moyen mouvement
, avec une vitesse angulaire égale au moyen mouvement 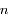 de la particule. On note
de la particule. On note 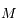 l'angle entre la ligne
l'angle entre la ligne 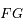 et la direction du péricentre de la particule (c'est donc l'
et la direction du péricentre de la particule (c'est donc l'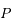 et on a
et on a 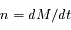 ).
).
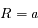 avec la Terre au foyer
avec la Terre au foyer 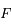 , et uniforme par rapport à
, et uniforme par rapport à 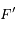 (appelé l'équant). Le modèle de Ptolémée était donc du premier ordre en excentricité, et le triomphe de Kepler fut d'élaborer une théorie à l'ordre 2.
(appelé l'équant). Le modèle de Ptolémée était donc du premier ordre en excentricité, et le triomphe de Kepler fut d'élaborer une théorie à l'ordre 2.
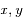 de
de 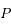 dans le repère orthonormé (
dans le repère orthonormé (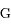 ,
,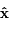 ,
,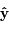 ) tel que
) tel que 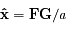 .
.
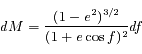 .
.
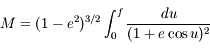 . Montrer à l'aide de cette relation que
. Montrer à l'aide de cette relation que 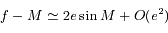 .
.
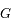 , la particule
, la particule 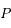 suit une orbite elliptique de demi-grand axe
suit une orbite elliptique de demi-grand axe 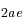 et de demi-petit axe
et de demi-petit axe 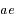 . Dans quel sens s'effectue ce mouvement et avec quelle période?
. Dans quel sens s'effectue ce mouvement et avec quelle période?
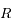 la distance entre
la distance entre 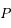 et le centre
et le centre 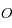 de l'ellipse. Montrer que
de l'ellipse. Montrer que 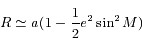 .
.
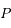 est alors un cercle centré sur
est alors un cercle centré sur 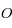 , et que l'angle
, et que l'angle 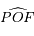 est confondu avec l'anomalie excentrique
est confondu avec l'anomalie excentrique 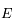 .
.
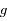 l'angle
l'angle 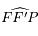 , où
, où 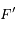 est le second foyer (vide) de l'ellipse. Ecrire
est le second foyer (vide) de l'ellipse. Ecrire 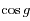 et en déduire que
et en déduire que 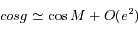 . On rappelle que
. On rappelle que 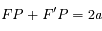 , et on utilisera le développement:
, et on utilisera le développement: 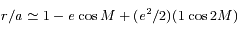 (voir cet
(voir cet 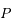 , vu du foyer
, vu du foyer 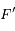 , est uniforme avec une vitesse angulaire égale au moyen mouvement
, est uniforme avec une vitesse angulaire égale au moyen mouvement 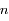 . Que peut-on dire des droites
. Que peut-on dire des droites 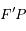 et
et 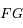 ?
?
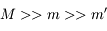 (qui constitue ce que l'on appelle un problème de Kepler perturbé).
(qui constitue ce que l'on appelle un problème de Kepler perturbé).
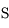 de masse
de masse 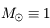 , de Jupiter
, de Jupiter 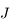 de masse
de masse 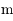 petite devant 1 (
petite devant 1 (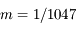 ) et d'un troisième corps
) et d'un troisième corps 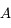 de masse
de masse 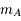 petite devant
petite devant 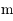 (par exemple un astéroïde ou une sonde spatiale). On note
(par exemple un astéroïde ou une sonde spatiale). On note 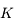 la constante de gravitation universelle,
la constante de gravitation universelle, 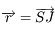 ,
, 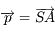 , et
, et 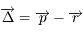 .
.
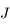 (c'est-à-dire de
(c'est-à-dire de 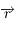 ).
).
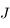 si la quantité
si la quantité 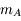 est négligeable?
est négligeable?
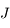 est circulaire (c'est-à-dire que
est circulaire (c'est-à-dire que 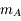 est négligeable et que
est négligeable et que 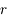 est constant). Montrer que l'équation du mouvement héliocentrique de
est constant). Montrer que l'équation du mouvement héliocentrique de 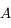 (c'est-à-dire de
(c'est-à-dire de 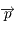 ) est
) est 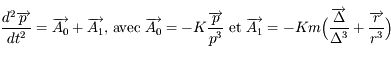 .
.
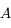 (c'est-à-dire de
(c'est-à-dire de 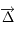 ) est
) est 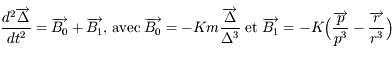 .
.
 définie par
définie par 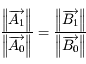 . On va voir notamment qu'elle a presque la forme d'une sphère,
appelée sphère d'influence de Jupiter. Justifier cette appellation en expliquant ce qui se passe pour le mouvement de
. On va voir notamment qu'elle a presque la forme d'une sphère,
appelée sphère d'influence de Jupiter. Justifier cette appellation en expliquant ce qui se passe pour le mouvement de 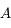 lorsque celui-ci est respectivement très à
l'intérieur ou très à l'extérieur de cette sphère.
lorsque celui-ci est respectivement très à
l'intérieur ou très à l'extérieur de cette sphère.
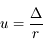 et
et 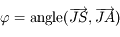 . Montrer que l'on a
. Montrer que l'on a 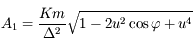 .
.
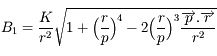 .
.
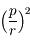 et
et 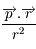 en fonction de
en fonction de 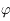 et
et 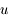 , montrer que
, montrer que 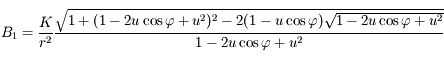 .
.
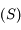 peut s'écrire
peut s'écrire 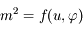 , et donner l'expression de
, et donner l'expression de 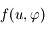 .
.
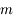 est petit devant 1, on peut considérer que, sur la surface
est petit devant 1, on peut considérer que, sur la surface 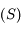 ,
, 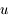 est également petit. Montrer que le développement de
est également petit. Montrer que le développement de 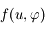 suivant les puissances de
suivant les puissances de 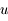 , limité à son terme de plus bas degré vaut
, limité à son terme de plus bas degré vaut 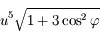 . Justifier alors le mot sphère dans l'expression sphère d'influence qui désigne la surface
. Justifier alors le mot sphère dans l'expression sphère d'influence qui désigne la surface 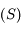 .
.
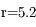 UA.
UA.
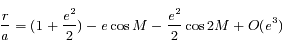
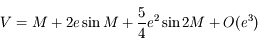
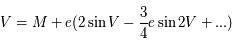 .
.
![V = M + \Sigma_{j=1}^\infty \frac{e^j}{j!} \frac{d^{j-1}}{dM^{j-1}} \Big{[} 2 \sin M - \frac{3}{4} e \sin 2M + ... \Big{]}^j](../pages_develop-appli/equations_develop-appli/equation56.png) .
.
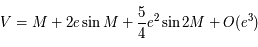 en développant la formule ci-dessus au second ordre.
en développant la formule ci-dessus au second ordre.
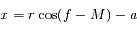 ,
, 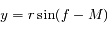
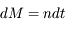
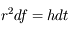 , avec
, avec 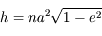 .
.
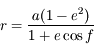 .
.
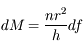 .
.
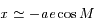 ,
, 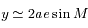 et
et 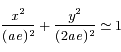 .
.
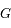 est en orbite circulaire autour de
est en orbite circulaire autour de 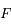 ,
, 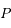 est en orbite autour de
est en orbite autour de 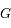 dans le sens opposé. La période est la même
dans le sens opposé. La période est la même 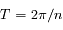 .
.
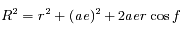 donc
donc 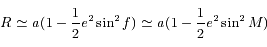 .
.
 , la trajectoire de
, la trajectoire de 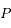 est ainsi un cercle de centre
est ainsi un cercle de centre 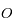 et l'angle
et l'angle 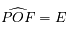
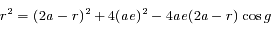
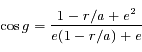 .
.
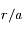 ,
, 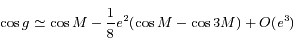 .
.
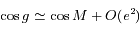 et
et 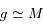 à l'ordre
à l'ordre  .
.
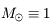 :
: 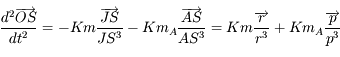 .
.
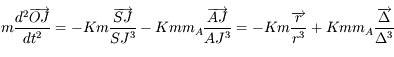 et
et 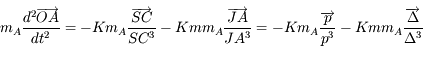 .
.
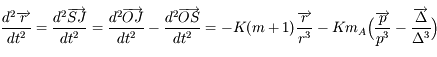 .
.
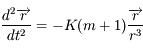 . C'est le problème de Kepler et le mouvement de
. C'est le problème de Kepler et le mouvement de 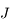 est une conique de foyer
est une conique de foyer 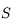 parcourue selon la loi des aires.
parcourue selon la loi des aires.
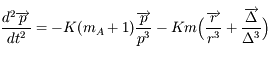 et
et 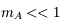 donc
donc 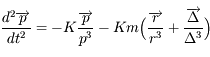
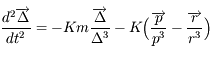 .
.
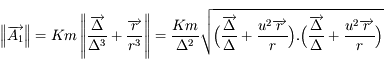
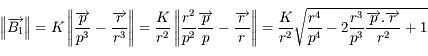
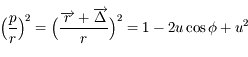 et
et 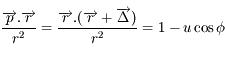 .
.
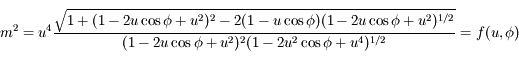
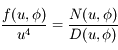 . On remarque que
. On remarque que 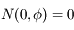 et
et 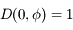 . Donc en développant
. Donc en développant 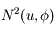 jusqu'au terme
jusqu'au terme 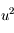 , on obtient
, on obtient 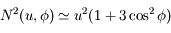 .
.
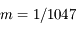 ,
, 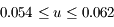 ,
, 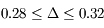 UA.
UA.