 |  |  |  |  |  |
Les outils mathématiques en astronomie
Ex : Séries du problème des 2-corps |
Séries du problème des 2-corpsDifficulté : ☆☆ Temps : 1h
IntroductionQuand on intègre le problème des 2-corps, la loi des aires permet d'écrire:
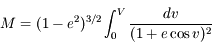
On utilisant cette relation et en négligeant les termes d'ordre supérieur ou égal à 3 en excentricité, montrer que l'on a:
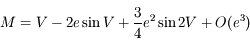
On sait que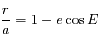 
et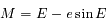 
(
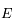est l'anomalie excentrique). En déduire le développement de 
en puissance de 
et en fonction de 
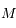(limité à l'ordre 2)
RemarqueDans cette dernière question, le calcul est fait "en crabe", il faut donc veiller à la discussion sur l'ordre en excentricité. Plus généralement, tous ces calculs supposent l'existence des développements recherchés. Cette supposition et l'unicité ont permis d'éviter de se soucier des conditions d'application des théorèmes utilisés.
 |  |
et intégrer le développement obtenu. Mutiplier enfin par celui de 
. Dans ces calculs, on prend soin de se limiter à l'ordre 2.
en 
au voisinage de 
, c'est-à-dire, écrire: 
.
n'est utile que jusque l'ordre 1 !
.
en fonction de 
(limité à l'ordre 2 en 
).
à l'ordre 0 (obtenu précédemment).
à l'ordre 1 et 
à l'ordre 0 (obtenus précédemment).
est obtenu de la manière suivante: 
. Attention à la discussion sur l'ordre à chaque étape du calcul.
