Ex: Sphère d'influence

Auteurs: Alain Vienne, S. Renner

Auteurs: S. Renner, A. Vienne

Sphère d'influence

Difficulté : ☆☆ Temps : 3h

Introduction

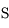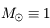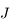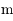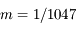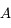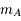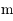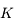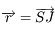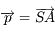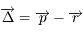On considère le système gravitationnel formé du Soleil $S$ de masse $M_\odot \equiv 1$ , de Jupiter de masse $m$ petite devant 1 ( m=1/1047 ) et d'un troisième corps de masse $m_{A}$ petite devant $m$ (par exemple un astéroïde ou une sonde spatiale). On note la constante de gravitation universelle, $\overrightarrow{r}=\overrightarrow{SJ}$ , $\overrightarrow{p}=\overrightarrow{SA}$ , et $\overrightarrow{\Delta}=\overrightarrow{p}-\overrightarrow{r}$ .

Question 1)

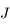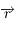Ecrire les équations du mouvement héliocentrique de (c'est-à-dire de $\overrightarrow{r}$ ).

Solution

Question 2)

Quelle est la nature du mouvement de 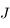si la quantité 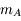$m_{A}$ est négligeable?

Solution

Question 3)

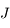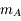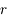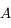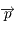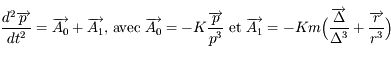On suppose désormais que le mouvement de est circulaire (c'est-à-dire que m_A est négligeable et que est constant). Montrer que l'équation du mouvement héliocentrique de (c'est-à-dire de $\overrightarrow{p}$ ) est $\frac{d^{2}\overrightarrow{p}}{dt^{2}}=\overrightarrow{A_{0}} + \overrightarrow{A_{1}} \textrm{, avec } \overrightarrow{A_{0}}=-K\frac{\overrightarrow{p}}{p^{3}} \textrm{ et } \overrightarrow{A_{1}}=-Km \Big{(} \frac{\overrightarrow{\Delta}}{\Delta^{3}}+ \frac{\overrightarrow{r}}{r^3} \Big{)}$ .

Solution

Question 4)

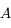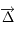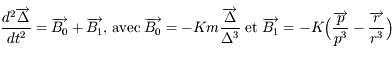Montrer que l'équation du mouvement jovicentique de (c'est-à-dire de $\overrightarrow{\Delta}$ ) est $\frac{d^{2}\overrightarrow{\Delta}}{dt^{2}}= \overrightarrow{B_{0}}+ \overrightarrow{B_{1}} \textrm{, avec } \overrightarrow{B_{0}}=-Km\frac{\overrightarrow{\Delta}} {\Delta^{3}} \textrm{ et } \overrightarrow{B_{1}}=-K \Big{(} \frac{\overrightarrow{p}}{p^{3}}-\frac{\overrightarrow{r}}{r^3} \Big{)}$ .

Solution

Question 5)

Dans la suite, on cherche à étudier la surface 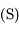$(S)$ définie par 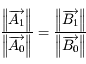$\frac{\left\Vert \overrightarrow{A_{1}}\right\Vert } {\left\Vert \overrightarrow{A_{0}}\right\Vert } =\frac{\left\Vert \overrightarrow{B_{1}}\right\Vert } {\left\Vert \overrightarrow{B_{0}}\right\Vert }$ . On va voir notamment qu'elle a presque la forme d'une sphère, appelée sphère d'influence de Jupiter. Justifier cette appellation en expliquant ce qui se passe pour le mouvement de 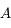lorsque celui-ci est respectivement très à l'intérieur ou très à l'extérieur de cette sphère.

Solution

Question 6)

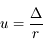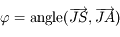On pose $\displaystyle u=\frac{\Delta}{r}$ et $\varphi=\textrm{angle}(\overrightarrow{JS},\overrightarrow{JA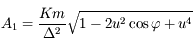})$ . Montrer que l'on a 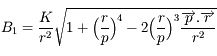$A_{1}=\frac{Km}{\Delta^{2}}\sqrt{1-2u^{2}\cos\varphi+u^{4}}$ .

Solution

Question 7)

Montrer que l'on a $B_{1}=\frac{K}{r^{2}}\sqrt{1+\Big{(}\frac{r}{p}\Big{)}^{4}-2\Big{(} \frac{r}{p}\Big{)}^{3} \frac{\overrightarrow{p}.\overrightarrow{r}}{r^{2}}}$ .

Solution

Question 8)

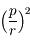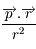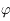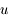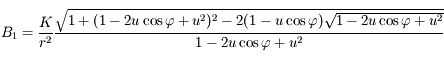En exprimant $\displaystyle \Big{(} \frac{p}{r} \Big{)}^{2}$ et $\displaystyle \frac{\overrightarrow{p}.\overrightarrow{r}}{r^{2}}$ en fonction de $\varphi$ et , montrer que $B_{1}=\frac{K}{r^{2}}\frac{\sqrt{1+(1-2u\cos\varphi+u^{2})^{2} -2(1-u\cos\varphi)\sqrt{1-2u\cos\varphi+u^{2}}}}{1-2u\cos\varphi+u^{2}}$ .

Solution

Question 9)

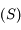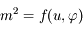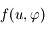En déduire que l'équation de la surface (S) peut s'écrire $m^{2}=f(u,\varphi)$ , et donner l'expression de $f(u,\varphi)$ .

Solution

Question 10)

Puisque 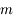est petit devant 1, on peut considérer que, sur la surface 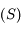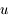(S) , est également petit. Montrer que le développement de 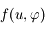$f(u,\varphi)$ suivant les puissances de 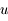, limité à son terme de plus bas degré vaut 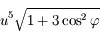$\displaystyle u^{5}\sqrt{1+3\cos^2\varphi}$ . Justifier alors le mot sphère dans l'expression sphère d'influence qui désigne la surface (S) .

Solution

Question 11)

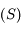Calculer le rayon de la sphère d'influence de Jupiter sachant que 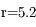$r=5.2$ UA.

Solution