Auteur: S. Renner

 Séries du problème des 2-corps (Lagrange)
Séries du problème des 2-corps (Lagrange)
Difficulté : ☆☆
Temps : 1h
Question 1)
On utilisant cette relation et en négligeant les termes d'ordre supérieur ou égal à 3 en excentricité, montrer que l'on a:
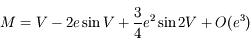
Aide
Développer d'abord 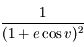 et intégrer le développement obtenu. Mutiplier enfin par celui de
et intégrer le développement obtenu. Mutiplier enfin par celui de 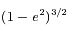 . Dans ces calculs, on prend soin de se limiter à l'ordre 2.
. Dans ces calculs, on prend soin de se limiter à l'ordre 2.
Question 2)
Utiliser le théorème d'inversion de Lagrange pour montrer que 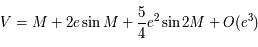 .
.
Solution
D'après la question précédente, on a donc : 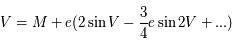 .
.
Le théorème d'inversion de Lagrange permet d'écrire : ![V = M + \Sigma_{j=1}^\infty \frac{e^j}{j!} \frac{d^{j-1}}{dM^{j-1}} \Big{[} 2 \sin M - \frac{3}{4} e \sin 2M + ... \Big{]}^j](../pages_develop-appli/equations_develop-appli/equation56.png) .
.
On obtient ainsi 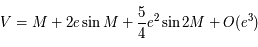 en développant la formule ci-dessus au second ordre.
en développant la formule ci-dessus au second ordre.


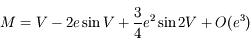
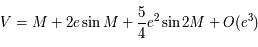 .
.