

Ex: Description épicyclique du mouvement keplerien |
Difficulté : ☆☆ Temps : 2h
Dans le problème à deux corps, on considère le mouvement d'une particule 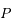 sur une ellipse de foyer
sur une ellipse de foyer 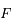 et de demi-grand axe
et de demi-grand axe 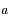 . On note
. On note 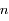 le moyen mouvement de la particule, et
le moyen mouvement de la particule, et 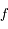 son anomalie vraie.
son anomalie vraie.
Soit 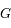 un point fictif tournant autour du foyer
un point fictif tournant autour du foyer 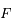 sur une orbite circulaire de rayon
sur une orbite circulaire de rayon 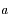 égal au demi-grand axe de
égal au demi-grand axe de 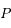 , avec une vitesse angulaire égale au moyen mouvement
, avec une vitesse angulaire égale au moyen mouvement 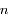 de la particule. On note
de la particule. On note 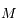 l'angle entre la ligne
l'angle entre la ligne 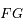 et la direction du péricentre de la particule (c'est donc l'anomalie moyenne de
et la direction du péricentre de la particule (c'est donc l'anomalie moyenne de 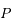 et on a
et on a 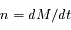 ).
).
Les questions 5 à 8 correspondent exactement à la représentation de Ptolémée du mouvement du Soleil autour de la Terre : un mouvement circulaire de rayon 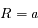 avec la Terre au foyer
avec la Terre au foyer 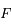 , et uniforme par rapport à
, et uniforme par rapport à 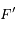 (appelé l'équant). Le modèle de Ptolémée était donc du premier ordre en excentricité, et le triomphe de Kepler fut d'élaborer une théorie à l'ordre 2.
(appelé l'équant). Le modèle de Ptolémée était donc du premier ordre en excentricité, et le triomphe de Kepler fut d'élaborer une théorie à l'ordre 2.
Ecrire les coordonnées 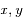 de
de 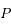 dans le repère orthonormé (
dans le repère orthonormé (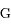 ,
,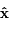 ,
,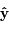 ) tel que
) tel que 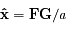 .
.
A partir de la loi des aires, montrer que: 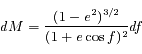 .
.
Ainsi en intégrant on obtient: 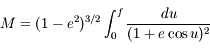 . Montrer à l'aide de cette relation que
. Montrer à l'aide de cette relation que 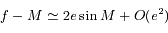 .
.
En déduire que par rapport à  , la particule
, la particule  suit une orbite elliptique de demi-grand axe
suit une orbite elliptique de demi-grand axe 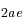 et de demi-petit axe
et de demi-petit axe 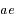 . Dans quel sens s'effectue ce mouvement et avec quelle période?
. Dans quel sens s'effectue ce mouvement et avec quelle période?
Soit 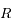 la distance entre
la distance entre 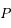 et le centre
et le centre  de l'ellipse. Montrer que
de l'ellipse. Montrer que 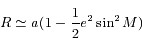 .
.
Montrer qu'au premier ordre en excentricité, la trajectoire de  est alors un cercle centré sur
est alors un cercle centré sur  , et que l'angle
, et que l'angle 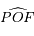 est confondu avec l'anomalie excentrique
est confondu avec l'anomalie excentrique 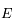 .
.
On note 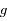 l'angle
l'angle 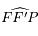 , où
, où 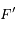 est le second foyer (vide) de l'ellipse. Ecrire
est le second foyer (vide) de l'ellipse. Ecrire 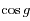 et en déduire que
et en déduire que 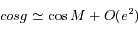 . On rappelle que
. On rappelle que 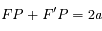 , et on utilisera le développement:
, et on utilisera le développement: 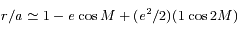 (voir cet exercice).
(voir cet exercice).
Ainsi, le mouvement de la particule 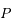 , vu du foyer
, vu du foyer 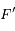 , est uniforme avec une vitesse angulaire égale au moyen mouvement
, est uniforme avec une vitesse angulaire égale au moyen mouvement 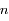 . Que peut-on dire des droites
. Que peut-on dire des droites 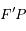 et
et 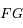 ?
?