Ex: Moindres carrés

Auteur: Jérôme Thiébaut

Moindres carrés

Difficulté : ☆☆ Temps : 20 min

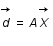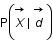On a le problème suivant accent(d;->)=A*accent(X;->) et on va chercher à déterminer la probabilité conditionnelle P(accent(X;->)*|*accent(d;->)) .

Question 1)

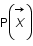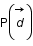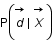Exprimer cette probabilité en fonction de P(accent(X;->)) , P(accent(d;->)) et P(accent(d;->)*|*accent(X;->)) en utilisant le théorème de Bayes.

Solution

Question 2)

On suppose que 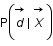P(accent(d;->)*|*accent(X;->)) suit une loi gaussienne multivariée de matrice de variance covariance 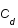C_d . Ecrire cette loi.

Aide Solution

Question 3)

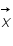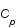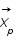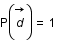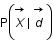On suppose que le vecteur accent(X;->) suit lui aussi une loi gaussienne de matrice de variance covariance C_p et de moyenne accent(X_p;->) (a priori sur la solution, sur son spectre de puissance...) et que P(accent(d;->))=1 . Exprimer P(accent(X;->)*|*accent(d;->)) .

Solution

Question 4)

Montrer que chercher les paramètres physiques les plus probables revient à résoudre la méthode des moindres carrés généralisés soit à trouver 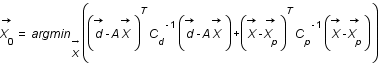accent(X_0;->)=argmin_(accent(X;->))*(((accent(d;->)-A*accent(X;->))^T*C_d^(-1)*(accent(d;->)-A*accent(X;->))+(accent(X;->)-accent(X_p;->))^T*C_p^(-1)*(accent(X;->)-accent(X_p;->)))) .

Solution

Question 5)

Dans les cas simples, on n'a pas d'a priori sur accent(X;->) et on considère que les covariances sont nulles et les variances égales entre elles donc C_d=sigma*I où est la matrice identité. Que devient accent(X_0;->) ?

Aide Solution