Moindres carrés

Auteur: Jérôme Thiébaut

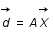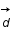On a très souvent accès en astrophysique à des données d (par exemple des spectres lumineux, des images CCD...) dont on veut extraire une quantité physique inconnue X (magnitude, masse, champ magnétique...). Si le problème est linéaire et si on connait les lois physiques sous jacentes, on peut modéliser le problème sous la forme , où est un vecteur contenant les données, 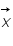est le vecteur des paramètres recherchés et 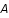est une matrice. Connaissant 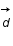on veut 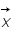, c'est ce qu'on appelle un problème inverse. Pour résoudre ce genre de problème on utilise très souvent la méthode des moindres carrés c'est à dire qu'on cherche le vecteur 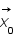qui minimise la quantité 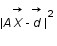.C'est ce qu'on appelle un ajustement. 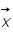On se propose ici de montrer que faire des à priori gaussiens sur les distributions de probabilité de et 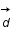revient à utiliser la méthode des moindres carrés.