images/logos_obspm_lille1.png

L'Astronomie dans l'apprentissage des Mathématiques

L'Astronomie dans l'apprentissage des Mathématiques

Statistiques et probabilités

Statistiques élémentaires

• Moyennes et estimations

• Ex: moyennes et estimations

• Propagation d'erreurs

• Ex: propagation d'erreurs

Ex: propagation d'erreurs

Auteur: Stéphane Erard

Erreurs sur une fonction

Difficulté : ☆☆ Temps : 30 min

Introduction

L'exercice consiste à dériver la précision des estimations de différentes fonctions spectrales.

Question 1)

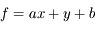
La fonction est une combinaison additive de variables : f = ax + y + b

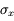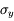où a et b sont des constantes, et x et y sont affectées des incertitudes $\sigma_x$ et $\sigma_y$ .

Quelle est l'incertitude associée 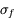$\sigma_f$ ?

Question 2)

On utilise maintenant une fonction multiplicative :

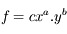f = cx^a . y^b où a, b et c sont des constantes.

Quelle est l'incertitude associée 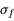$\sigma_f$ ?

Question 3)

Pour les cas plus compliqués où l'on connaît la forme analytique de la fonction, écrire la formulation générale.

Question 4)

On applique ces résultats à la situation suivante :

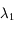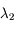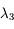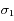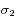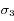On mesure les intensités a, b et c aux longueurs d'onde $\lambda_1$ , $\lambda_2$ et $\lambda_3$ situées autour d'une bande d'absorption, avec les incertitudes $\sigma_1$ , $\sigma_2$ et $\sigma_3$ .

Exemple de spectre infrarouge et définition des paramètres mesurés

Crédit : Astrophysique sur Mesure / Erard

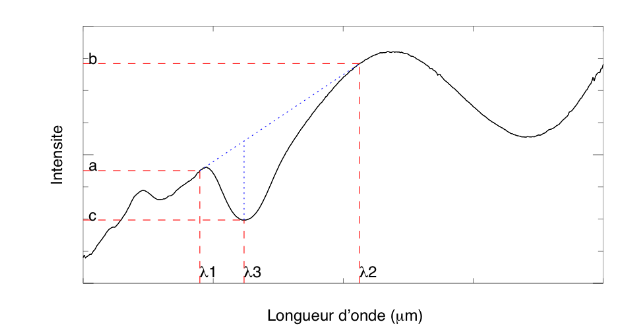
On estime le continuum (pente spectrale) autour de la bande d'absorption comme 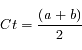$Ct = \frac{(a+b)}2$

et la profondeur de cette bande comme 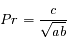$Pr = \frac c{\sqrt{ab}}$

Écrire les incertitudes sur ces quantités en fonction de celles des mesures.

Question 5)

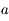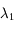On utilise maintenant la mesure d'éclairement pour estimer la magnitude à la longueur d'onde $\lambda_1$ .

Ecrire cette magnitude en fonction de 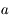et d'une constante d'échelle.

Question 6)

Ecrire l'incertitude sur cette magnitude en fonction de celle sur l'éclairement.