Auteur: Stéphane Erard

 Estimation d'une moyenne
Estimation d'une moyenne
Difficulté : ☆
Temps : 30 min
On mesure l'éclairement d'une étoile. La valeur "réelle" est notée 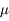 (celle que mesurerait un instrument parfait).
(celle que mesurerait un instrument parfait).
Pour obtenir une bonne estimation de cette quantité, une méthode usuelle est de pratiquer N mesures successives 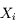 . On s'attend à ce que celles-ci se répartissent de façon gaussienne autour de la valeur
. On s'attend à ce que celles-ci se répartissent de façon gaussienne autour de la valeur 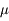 (théorème de la limite centrale).
(théorème de la limite centrale).
Question 1)
A partir de ces N estimations indépendantes de l'éclairement, dériver le résultat de la mesure : valeur estimée de la moyenne 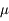 , et incertitude sur cette estimation.
, et incertitude sur cette estimation.
Solution
Le meilleur estimateur de l'éclairement de la source est la moyenne des mesures :
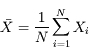
L'écart-type σ donne la dispersion des mesures :
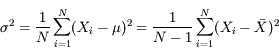
Le facteur N / (N-1) provient du fait qu'on doit utiliser dans le calcul un estimateur de la moyenne plutôt que la moyenne elle-même, et corrige du biais ainsi introduit.
La précision sur l'estimateur de la moyenne est l'erreur-type :
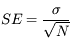
Le résultat est donc 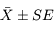 . En pratique, on peut utiliser
. En pratique, on peut utiliser 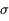 comme barre d'erreur "réaliste" sur le résultat pour éviter toute sur-interprétation.
comme barre d'erreur "réaliste" sur le résultat pour éviter toute sur-interprétation.
Question 2)
Plusieurs équipes ayant publié leurs résultats (maintenant notés 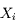 ), on veut en tirer la meilleure évaluation possible. Ce problème est équivalent à celui de mesures successives entachées d'incertitudes indépendantes
), on veut en tirer la meilleure évaluation possible. Ce problème est équivalent à celui de mesures successives entachées d'incertitudes indépendantes 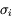 .
.
Application numérique : on a deux mesures indépendantes 100±5 et 94±20. Quelle est l'estimation résultante ?
Solution
Le meilleur estimateur de l'éclairement est la moyenne des mesures pondérées par leurs incertitudes :
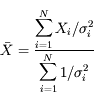
L'incertitude globale est :
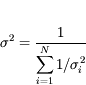
Elle est normalement égale à l'erreur-type. Si ce n'est pas le cas, cela indique qu'on a probablement négligé une erreur systématique.
Application numérique : la meilleure estimation est 100±5 (en conservant la précision des données d'origine). La moyenne arithmétique naïve (sans pondération par l'incertitude) 97±10 est particulièrement trompeuse dans ce cas : l'incertitude sur la deuxième mesure est ici si grande qu'elle ne contribue pas au résultat, mais ne le dégrade pas non plus.


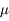 (celle que mesurerait un instrument parfait).
(celle que mesurerait un instrument parfait).
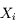 . On s'attend à ce que celles-ci se répartissent de façon gaussienne autour de la valeur
. On s'attend à ce que celles-ci se répartissent de façon gaussienne autour de la valeur 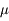 (théorème de la limite centrale).
(théorème de la limite centrale).
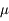 , et incertitude sur cette estimation.
, et incertitude sur cette estimation.
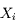 ), on veut en tirer la meilleure évaluation possible. Ce problème est équivalent à celui de mesures successives entachées d'incertitudes indépendantes
), on veut en tirer la meilleure évaluation possible. Ce problème est équivalent à celui de mesures successives entachées d'incertitudes indépendantes 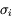 .
.