Equations différentielles linéaires
- Introduction
- Du premier ordre
- Transfert de rayonnement
- Ex: Transfert de rayonnement
- Equation de Kepler
- Ex: equation de Kepler
- Du second ordre
- Pendule et équation de Mathieu
- Ex: Pendule et équation de Mathieu
- Longueur de Debye
- Ex: Détermination du potentiel dans une sphère de Debye
- Le problème de 2 corps
- Ex : le problème de 2 corps
- Train gravitationnel
- Ex: Train gravitationnel
- Pendule de Foucault
- Ex: Pendule de Foucault
Introduction
On trouvera dans cette partie les exercices suivants :
- Problèmes simples de transfert de rayonnement (équations différentielles linéaires du premier ordre)
- La démonstration de l'équation de Kepler (équations différentielles du premier ordre)
- Une discussion sur la stabilité d'un pendule perturbé
- Résolution du problème de 2 corps (équations différentielles linéaires du second ordre)
- Détermination du potentiel dans une sphère de Debye (équations différentielles du second ordre)
- Train gravitationnel (équations différentielles du second ordre)
- Le pendule de Foucault
Du premier ordre
Auteurs: Stéphane Erard, Marc Fouchard
Transfert de rayonnement
Le transfert de rayonnement décrit l'interaction du rayonnement électromagnétique et de la matière. Cette discipline permet notamment d'analyser la propagation de la lumière à travers un milieu gazeux et joue donc un rôle fondamental dans l'analyse des spectres stellaires et des atmosphères planétaires.
L'équation de transfert fait le bilan énergétique relatif au transport de photons dans un milieu. Comme toujours, on écrit que la quantité à laquelle on s'intéresse varie proportionnellement à sa valeur sur un intervalle suffisamment petit pour que le coefficient soit constant :
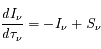
où  est l'intensité lumineuse à la fréquence
est l'intensité lumineuse à la fréquence  ,
,  est la profondeur optique du milieu,
est la profondeur optique du milieu, 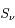 est la fonction source, égale au rapport du coefficient d'émission au coefficient d'absorption du milieu traversé.
est la fonction source, égale au rapport du coefficient d'émission au coefficient d'absorption du milieu traversé.
En intégrant cette équation le long du trajet du faisceau lumineux, on a :
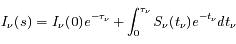
où 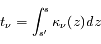 est l'épaisseur optique entre les points s' et s, et
est l'épaisseur optique entre les points s' et s, et 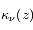 est le coefficient d'absorption du milieu en z.
est le coefficient d'absorption du milieu en z.
On veut résoudre cette équation pour connaître l'intensité en fonction des propriétés du milieu. Les exercices suivants étudient des situations particulières qu'on rencontre fréquemment.
Ex: Transfert de rayonnement
Auteur: Stéphane Erard
 Atmosphère planétaire en visible
Atmosphère planétaire en visible
Difficulté : ☆
Temps : 15 min
Question 1)
On se place dans l'approximation "plan-parallèle" où on néglige localement la courbure de la planète. Déterminer l'expression de l'intensité lumineuse reçue à la surface de la Terre ou de Mars, dans le cas où le Soleil est au zénith.
figure 1
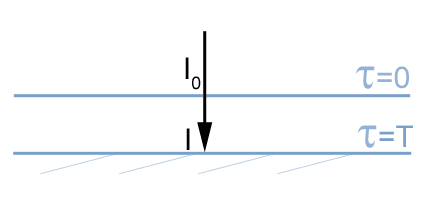
On s'intéresse au flux descendant, le Soleil étant à la verticale.
Ces deux planètes ont une atmosphère fine et sont suffisamment froides pour ne pas émettre en visible. Le terme de source est donc nul, et l'atmosphère ne fait qu'absorber (ou diffuser) la lumière incidente.
Question 2)
Cas où le Soleil est vu sous un certain angle (la profondeur optique est toujours mesurée à la verticale).
figure 2
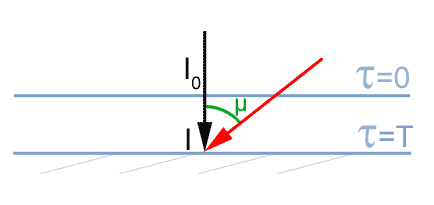
Le Soleil est cette fois vu sous un certain angle.
Auteur: Stéphane Erard
 Face nuit de Vénus
Face nuit de Vénus
Difficulté : ☆☆
Temps : 30 min
Question 1)
Vénus a une température de surface très élevée, de l'ordre de 740 K, qui ne varie quasiment pas au cours de la journée. La température diminue avec l'altitude, pour s'établir à environ 230 K au sommet des nuages côté nuit.
Quelle est l'allure du spectre infrarouge de la face nuit de Vénus ?
figure 3
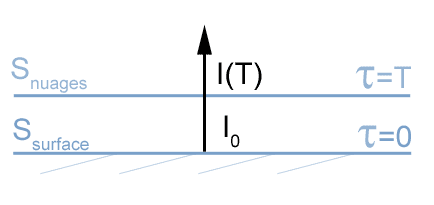
On s'intéresse cette fois au flux montant, qu'on mesure au sommet de l'atmosphère.
Question 2)
A quoi est due la température de surface ?
Question 3)
Il existe néanmoins d'étroites régions spectrales entre 1 et 2,5 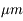 où l'atmosphère n'est pas entièrement opaque. Ecrire le flux émergent dans ces régions spectrales où l'atmosphère est semi-transparente.
où l'atmosphère n'est pas entièrement opaque. Ecrire le flux émergent dans ces régions spectrales où l'atmosphère est semi-transparente.
Question 4)
La figure 4 donne un spectre observé de la face nuit de Vénus. Interpréter le flux spectral mesuré à la lumière des questions précédentes.
figure 4
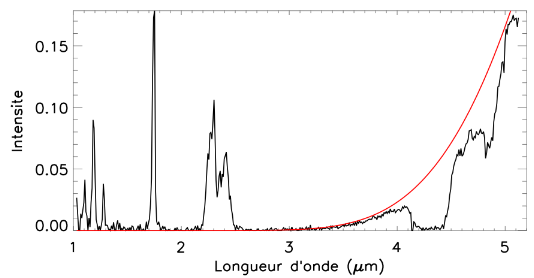
Spectre infrarouge de Vénus mesuré sur la face nuit (instrument Virtis /
Venus-Express). La courbe rouge est un corps noir à 233 K.
Crédit :
ESA / LESIA
Equation de Kepler
Auteur: Marc fouchard
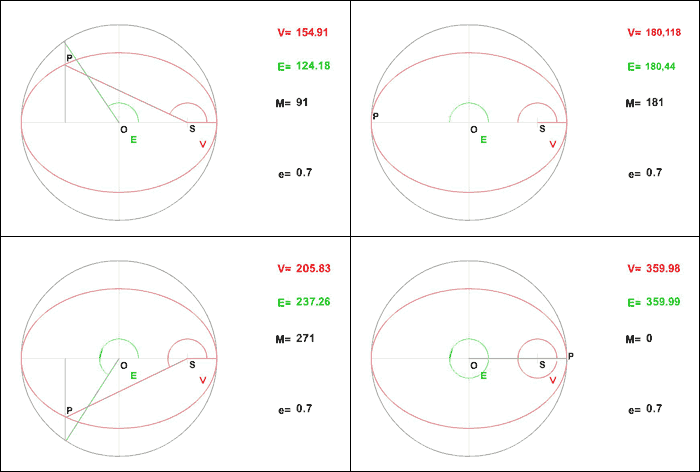
On reprend les résultats obtenus dans l'exercice sur la résolution du problème de 2 corps. Le but est d'obtenir à partir de ces résultats l'équation de Kepler. Cette équation est fondamentale en mécanique céleste puisque c'est elle qui fait le lien entre le temps et la position de l'objet sur son orbite (voir la figure).
Les trois anomalies
Ex: equation de Kepler
 équation de Kepler
équation de Kepler
Difficulté : ☆☆☆
Temps : 1h
Question 1)
On considère le mouvement d'un corps ponctuel  de masse négligeable soumise à l'attraction universelle d'un corps de masse
de masse négligeable soumise à l'attraction universelle d'un corps de masse  situé au centre
situé au centre 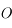 du repère de référence. La force s'appliquant à
du repère de référence. La force s'appliquant à 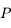 est donnée par :
est donnée par : 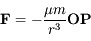 , où la notation en gras dénote des vecteurs,
, où la notation en gras dénote des vecteurs, 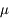 est la constante universelle de la gravitation, et
est la constante universelle de la gravitation, et 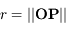 . Les coordonnées de
. Les coordonnées de 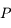 dans le repère tournant étant
dans le repère tournant étant 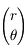 , on a vu dans l'exercice du problème de 2 corps que la solution des équations du mouvement est :
, on a vu dans l'exercice du problème de 2 corps que la solution des équations du mouvement est :
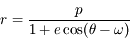 ,
,
où 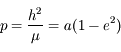 ,
, 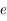 est l'excentricité de la trajectoire,
est l'excentricité de la trajectoire, 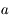 est le demi-grand axe et
est le demi-grand axe et 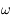 est l'argument du péricentre
est l'argument du péricentre
On a vu aussi que la norme du moment angulaire 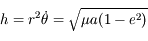 est une constante du mouvement, ainsi que l'intégrale de l'énergie donnée par
est une constante du mouvement, ainsi que l'intégrale de l'énergie donnée par 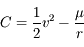 , où
, où  est la norme de la vitesse de
est la norme de la vitesse de  .
.
Dans le repère tournant on a vu que 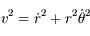 .
.
Entre un instant  et l'instant
et l'instant 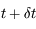 , le point
, le point 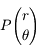 s'est déplacé au point
s'est déplacé au point 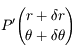 . En déduire, l'aire élémentaire
. En déduire, l'aire élémentaire 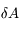 balayée par le rayon vecteur
balayée par le rayon vecteur 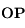 pendant l'intervalle de temps
pendant l'intervalle de temps 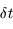 . On ne retiendra que les quantités d'ordre 1.
. On ne retiendra que les quantités d'ordre 1.
Question 2)
En déduire que le mouvement moyen 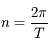 , où
, où 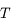 est la période du mouvement est tel que
est la période du mouvement est tel que 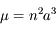 .
.
Cette relation correspond à la troisième loi de Kepler.
Question 3)
Après avoir vérifier que 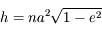 , montrer que:
, montrer que:
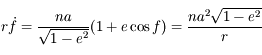
et que:
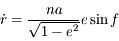
où 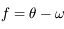 .
. 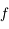 s'appelle l'anomalie vraie et correspond à l'angle entre le péricentre et
s'appelle l'anomalie vraie et correspond à l'angle entre le péricentre et  vu depuis le foyer
vu depuis le foyer 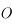 .
.
Question 4)
Après avoir montrer que 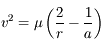 , en déduire que l'intégrale de l'énergie
, en déduire que l'intégrale de l'énergie 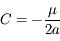 .
.
Question 6)
Montrer, en utilisant l'expression de 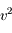 que
que 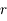 vérifie l'équation différentielle suivante:
vérifie l'équation différentielle suivante:
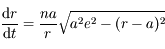
Question 7)
En déduire que l'anomalie excentrique 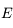 vérifie l'équation différentielle:
vérifie l'équation différentielle:
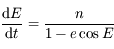 .
.
On part de 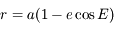 , et on utilise la relation
, et on utilise la relation 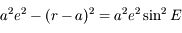 .
.
Du second ordre
Auteurs: Arnaud Beck, Marc Fouchard, S. Renner, Florent Deleflie, Alain Vienne
Pendule et équation de Mathieu
Auteur: Alain Vienne
Beaucoup de modèles dynamiques, après maintes transformations (hypothèses simplificatrices, moyennisations, ...), ressemblent au modèle du pendule (masse à une distance constante d'un point fixe sous l'effet de la pesanteur). Ici nous allons nous intéresser à un type d'équation du pendule correspondant à l'équation de Mathieu:
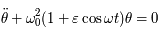
Si 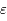 est nul, c'est l'équation d'un pendule simple pour de petites oscillations. Dans ce cas,
est nul, c'est l'équation d'un pendule simple pour de petites oscillations. Dans ce cas, 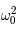 est inversement proportionnel à la longueur du pendule. On rappelle que la période
est inversement proportionnel à la longueur du pendule. On rappelle que la période 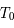 est alors
est alors 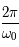 .
.
Ici 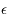 est un petit paramètre. On dit que le modèle du pendule simple est perturbé. L'équation de Mathieu est un cas particulier de l'équation
est un petit paramètre. On dit que le modèle du pendule simple est perturbé. L'équation de Mathieu est un cas particulier de l'équation
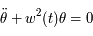
où  est une fonction périodique de période
est une fonction périodique de période  qui est utilisée en Mécanique Céleste pour l'étude du mouvement de la Lune.
qui est utilisée en Mécanique Céleste pour l'étude du mouvement de la Lune.
De manière plus ludique, ces équations peuvent modéliser le mouvement d'une balançoire dont le passager se lève et s'assied (périodiquement) afin de s'élancer. Le fait de se lever et de s'assoir régulièrement revient à déplacer le centre de gravité du passager et donc, revient à faire varier périodiquement la longueur du pendule (ici la balançoire).
L'exercice qui suit ne résoud pas l'équation différentielle. Il cherche simplement à savoir dans quelles conditions la solution est bornée ou non (problème de stabilité). Il est insipré du théorème de Gustave Floquet (1847-1920).
Ex: Pendule et équation de Mathieu
Auteur: Alain Vienne
 Exercice
Exercice
Difficulté : ☆☆
Temps : 2h30
On considère l'équation différentielle suivante (équation de Mathieu):
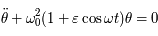
Où 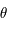 est une fonction du temps
est une fonction du temps  . Cette équation dépend des paramètres
. Cette équation dépend des paramètres 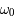 ,
, 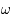 et
et 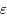 .
.
On souhaite déterminer dans quelles conditions la solution est bornée ou non.
Question 1)
Ecrire l'équation de Mathieu comme une équation différentielle du premier ordre:
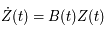
où 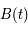 est une matrice
est une matrice 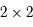 réelle. Donner la signification de la nouvelle inconnue
réelle. Donner la signification de la nouvelle inconnue 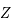 (par rapport à
(par rapport à 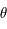 ).
).
Question 2)
On se donne une condition initiale 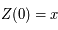 (on a
(on a 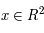 ). D'après le théorème de Cauchy l'équation différentielle a alors une solution unique que l'on note
). D'après le théorème de Cauchy l'équation différentielle a alors une solution unique que l'on note 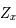
Monter que l'application 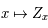 est linéaire.
est linéaire.
Question 4)
Pouvoir expliciter  , revient à obtenir toutes les solutions de l'équation différentielle.
, revient à obtenir toutes les solutions de l'équation différentielle.  est donc une inconnue. Montrer que
est donc une inconnue. Montrer que  vérifie le système suivant:
vérifie le système suivant:
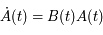
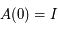
où 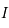 est la matrice identité.
est la matrice identité.
Question 5)
Montrer que pour tout système de la forme
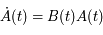
, on a le résultat suivant:
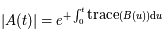
où 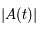 est le déterminant (d'ordre 2) de
est le déterminant (d'ordre 2) de 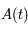 et
et 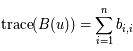 (somme des éléments diagonaux).
(somme des éléments diagonaux).
Question 7)
Montrer que:
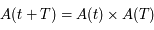
où 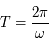
Question 8)
La matrice 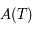 s'appelle la matrice de Floquet.
s'appelle la matrice de Floquet.
Montrer que les valeurs propres 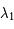 et
et 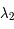 de la matrice de Floquet vérifient:
de la matrice de Floquet vérifient:
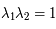
Question 9)
Ainsi, si ces valeurs propres sont réelles, l'une d'elle en valeur absolue est supérieure à  . Donc avec
. Donc avec 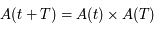 et une condition initale prise dans la direction du vecteur propre associé à cette valeur propre, la solution tendera vers l'infini.
et une condition initale prise dans la direction du vecteur propre associé à cette valeur propre, la solution tendera vers l'infini.
Montrer que sinon (valeurs propres complexes), les solutions sont bornées.
Question 10)
Dans notre cas (équation de Mathieu), 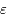 est petit. On peut alors montrer que la somme des valeurs propres de
est petit. On peut alors montrer que la somme des valeurs propres de 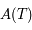 est la trace de la matrice
est la trace de la matrice 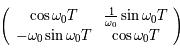 (ie: correspondant à celle trouvée dans le cas de perturbation nulle). Donc
(ie: correspondant à celle trouvée dans le cas de perturbation nulle). Donc
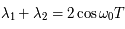
Montre que des solutions non bornées sont possibles que si la période 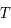 du forçage est telle que
du forçage est telle que
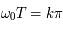
où 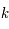 est un entier relatif.
est un entier relatif.
Longueur de Debye
Auteur: Arnaud Beck
Un plasma est une collection de particules chargées. Pour simplifier, considérons qu'il n'est composé que d'électrons de charge 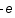 et d'ions de charge
et d'ions de charge 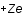 .
.
Un ion, considéré comme ponctuel, lorsqu'il est dans le vide crée autour de lui un potentiel 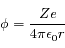 où
où 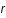 est la distance à l'ion. Ce potentiel est appelé le potentiel Coulombien.
est la distance à l'ion. Ce potentiel est appelé le potentiel Coulombien.
Dans un plasma, il en va différemment. En effet, il va attirer autour de lui des charges de signe opposé (les électrons) qui vont écranter son potentiel. La sphère d'électrons qui se forme autour de l'ion est appelée la sphère de Debye et son rayon est appelé la longueur de Debye. C'est un paramètre fondamental en physique des plasmas.
 Remarque
Remarque
Dans cet exercice, on propose de retrouver la valeur de ce rayon et la forme du potentiel à l'intérieur de la sphère de Debye.
Ex: Détermination du potentiel dans une sphère de Debye
Auteur: Arnaud Beck
 Détermination du potentiel dans une sphère de Debye
Détermination du potentiel dans une sphère de Debye
Le problème de 2 corps
Ex : le problème de 2 corps
Auteur: Marc Fouchard
 Le problème de 2 corps
Le problème de 2 corps
Difficulté : ☆☆
Temps : 2h
Question 1)
Montrer que 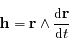 est une constante du mouvement. Cette constante s'appelle l'intégrale du moment angulaire.
est une constante du mouvement. Cette constante s'appelle l'intégrale du moment angulaire.
Question 4)
En utilisant les coordonnées polaires montrer que l' équation du mouvement revient à résoudre le système :
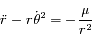
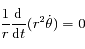
On remarquera que la deuxième équation correspond à l'intégrale du moment angulaire.
Train gravitationnel
Auteur: S. Renner
Date de création: 14 décembre 2009
L'accélération de la pesanteur dépend de la distance au centre de la Terre. Dans l'exercice qui suit, on va utiliser cette propriété pour imaginer un moyen de transport très rapide: en perçant un tunnel rectiligne entre 2 points A et B quelconques de la surface terrestre, un train roulant sans frottement dans ce tunnel pourrait parcourir très rapidement la distance entre A et B. La durée du trajet, de 42 minutes environ, est même indépendante des points A et B choisis.
Ex: Train gravitationnel
Auteur: S. Renner
 Train gravitationnel
Train gravitationnel
Difficulté : ☆
Temps : 1h
On assimile la Terre à une sphère sans rotation de rayon 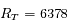 km et de masse volumique uniforme
km et de masse volumique uniforme 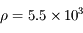
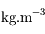 . Soit
. Soit 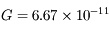 S.I. la contante de gravitation universelle. On imagine un tunnel rectiligne entre 2 points A et B quelconques de la surface terrestre, et un train roulant sans frottement dans ce tunnel. Partant de A sous l'action de la pesanteur, le wagon va accélérer jusqu'au milieu du tunnel, puis décélérer une fois atteinte la distance de moindre approche du centre 0 de la Terre (voir figure). Le train atteindra-t-il le point B, et si oui, en combien de temps?
S.I. la contante de gravitation universelle. On imagine un tunnel rectiligne entre 2 points A et B quelconques de la surface terrestre, et un train roulant sans frottement dans ce tunnel. Partant de A sous l'action de la pesanteur, le wagon va accélérer jusqu'au milieu du tunnel, puis décélérer une fois atteinte la distance de moindre approche du centre 0 de la Terre (voir figure). Le train atteindra-t-il le point B, et si oui, en combien de temps?
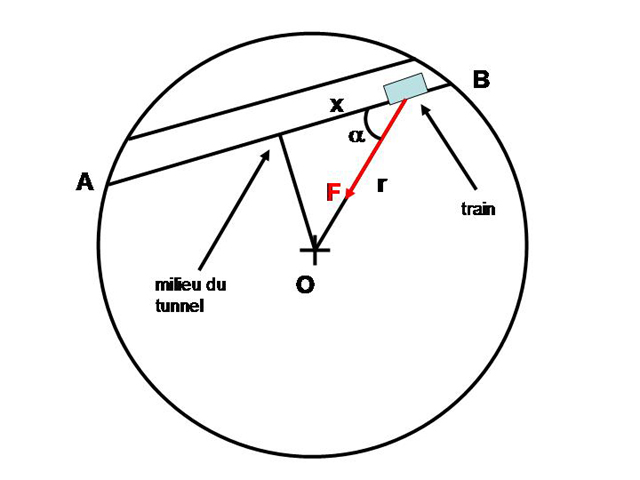
Tunnel rectiligne entre 2 points A et B de la surface terrestre. Le train est repéré par la coordonnée
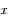
, sa distance au centre de la Terre est notée
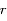
.
Question 3)
En déduire l'équation du mouvement du train dans le tunnel.
Question 4)
Le train peut-il atteindre le point B, et si oui, en combien de temps?
Pendule de Foucault
Florent Deleflie & Alain Vienne
Date de création: 21décembre 2010
Le pendule de Foucault est une expérience conçue pour mettre en évidence la rotation de la Terre, depuis un site terrestre d'observation. Son principe est basé sur la force de Coriolis qui existe dans tout réferentiel non galiléen, comme le référentiel terrestre d'observation. La réalisation de l'expérience est facilitée si la longueur du pendule est grande, comme sous le dôme d'une cathédrale par exemple. La première démonstration publique a eu lieu en 1851, sous la voûte du Panthéon, à Paris.
L'animation ci-dessous tient compte de toutes les forces sans les approximations qui seront faites dans l'exercice suivant.
Pendule de Foucault 
Ex: Pendule de Foucault
Auteur: Auteurs : Alain Vienne, Florent Deleflie.
 Pendule de Foucault
Pendule de Foucault
Difficulté : ☆☆
Temps : 1h
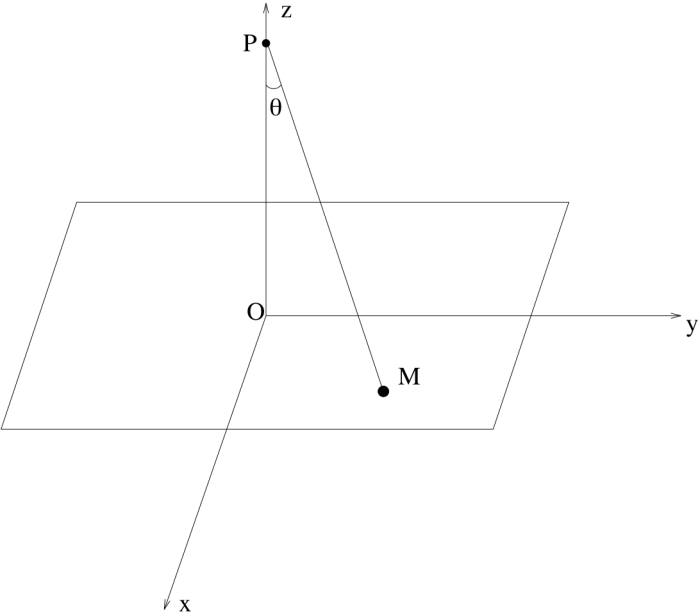
Le but de cet exercice est de reprendre la modélisation du pendule en tenant compte du fait que le repère terrestre n'est pas galiléen, mais est animé d'un mouvement de rotation de la Terre elle-même. La véritable motivation de l'exercice est la résolution de l'équation différentielle du mouvement.
On considère un pendule constitué d'un fil 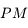 accroché en
accroché en 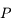 de longueur
de longueur 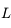 et d'une boule
et d'une boule 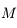 de masse
de masse 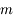 . L'espace est rapporté au système d'axes
. L'espace est rapporté au système d'axes 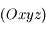 fixe dans le réferentiel lié à la Terre, l'axe
fixe dans le réferentiel lié à la Terre, l'axe 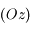 passant par
passant par 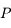 et le centre de la Terre (voir figures).
On se place dans le cas de faibles oscillations. On rappelle que dans ce cas, le mouvement de la boule
et le centre de la Terre (voir figures).
On se place dans le cas de faibles oscillations. On rappelle que dans ce cas, le mouvement de la boule 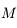 de coordonnées
de coordonnées 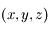 se fait dans le plan
se fait dans le plan 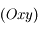 et que le module de la tension du fil
et que le module de la tension du fil 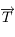 est
est 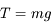 où
où 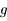 est l'accélération de la pesanteur. On note
est l'accélération de la pesanteur. On note 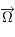 le vecteur rotation de la Terre et
le vecteur rotation de la Terre et 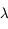 la latitude du lieu.
Le bilan des forces doit faire intervenir la force d'inertie de Coriolis, dont l'expression est
la latitude du lieu.
Le bilan des forces doit faire intervenir la force d'inertie de Coriolis, dont l'expression est 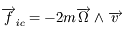 où
où 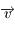 désigne la vitesse dans le repère
désigne la vitesse dans le repère 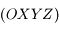 . Par contre, il n'y a pas lieu de tenir compte de la force d'inertie d'entrainement, car celle-ci est déjà incluse dans la définiton de la pesanteur, i.e. dans l'expression de
. Par contre, il n'y a pas lieu de tenir compte de la force d'inertie d'entrainement, car celle-ci est déjà incluse dans la définiton de la pesanteur, i.e. dans l'expression de 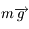 .
Une fois le bilan des forces effectué, on peut montrer que les composantes de la tension du fil dans
.
Une fois le bilan des forces effectué, on peut montrer que les composantes de la tension du fil dans 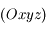 sont
sont 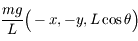 et que les composantes de la force de Coriolis sont
et que les composantes de la force de Coriolis sont 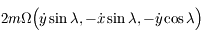 . D'après l'hypothèse faite sur la petitesse des oscillations, il n'y a pas lieu de considérer l'équation obtenue par projection sur
. D'après l'hypothèse faite sur la petitesse des oscillations, il n'y a pas lieu de considérer l'équation obtenue par projection sur 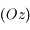 , celle-ci pouvant être considérée comme un terme correctif. On ne considère donc que les projections selon les deux autres directions, et en posant
, celle-ci pouvant être considérée comme un terme correctif. On ne considère donc que les projections selon les deux autres directions, et en posant 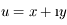 où
où 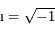 , et en posant aussi
, et en posant aussi 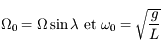 on peut montrer que l'équation du mouvement, complexe, se met sous la forme :
on peut montrer que l'équation du mouvement, complexe, se met sous la forme : 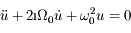 .
.
Schéma du pendule dans l'espace
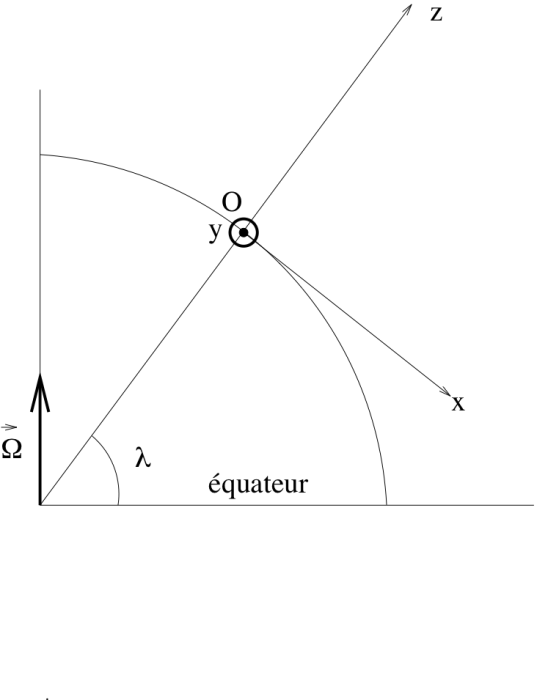
Le pendule vu dans le repère de l'observateur, et en coupe verticale.
Auteur: A. Vienne, F. Deleflie
 Pendule de Foucault
Pendule de Foucault
L'équation différentielle du mouvement qu'on se propose de résoudre est :
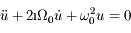
Question 1)
Ecrire le discriminant réduit de cette équation.
Question 2)
Déterminer les solutions de l'équation caractéristiques, et en déduire la forme générale de la solution de l'équation différentielle.
Question 3)
Particulariser la solution précédente en considérant qu'à l'instant initial, le mobile se trouve en 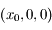 avec une vitesse initiale nulle.
avec une vitesse initiale nulle.
Question 5)
Simplifier l'expression de la solution trouvée en négligeant 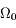 devant
devant 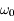 . Interpréter.
. Interpréter.
Réponses aux exercices
pages_ed-01/ex-transfert-de-rayonnement.html
Exercice
'Atmosphère planétaire en visible'
-
Question 1
Aide :
Ces deux planètes ont une atmosphère fine et sont suffisamment froides pour ne pas émettre en visible. Le terme de source est donc nul, et l'atmosphère ne fait qu'absorber (ou diffuser) la lumière incidente.
Solution :
Soit 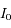 l'intensité reçue au sommet de l'atmosphère (flux solaire).
l'intensité reçue au sommet de l'atmosphère (flux solaire).
Avec les hypothèses ci-dessus, l'équation de transfert s'écrit comme une équation différentielle de premier ordre sans second membre :
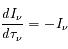 soit :
soit : 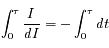
On trouve 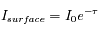
-
Question 2
Solution :
Si le Soleil n'est pas au zénith, le problème est identique mais le chemin parcouru dans l'atmosphère est plus long d'un facteur 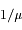 , où
, où 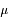 est le cosinus de l'angle d'incidence.
est le cosinus de l'angle d'incidence.
La solution est alors : 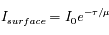
On voit que l'absorption totale augmente quand le Soleil est plus bas sur l'horizon.
Cette loi d'absorption/diffusion très élémentaire est appelée loi de Beer-Lambert.
pages_ed-01/ex-transfert-de-rayonnement.html
Exercice
'Face nuit de Vénus'
-
Question 1
Solution :
La surface comme les nuages émettent en première approximation un spectre de corps noir, dont le maximum est donné par la loi de déplacement de Wien, 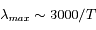 , soit environ 4
, soit environ 4 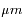 pour la surface, et 12
pour la surface, et 12 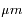 pour les nuages. On pourrait s'attendre à ce que l'émission de surface, beaucoup plus élevée, domine le spectre (voir les propriétés du corps noir).
pour les nuages. On pourrait s'attendre à ce que l'émission de surface, beaucoup plus élevée, domine le spectre (voir les propriétés du corps noir).
Cependant l'atmosphère de Vénus est extrêmement absorbante dans la plus grande partie du spectre, on a donc 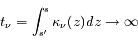 (cas optiquement épais). L'équation de transfert s'écrit dans ce cas :
(cas optiquement épais). L'équation de transfert s'écrit dans ce cas :
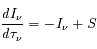 soit
soit 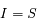 au sommet de l'atmosphère, où S est le spectre de corps noir émis par les nuages. La température de brillance (correspondant à l'émission thermique) de la face nuit de Vénus est donc de 230 K, dans la plus grande partie du spectre.
au sommet de l'atmosphère, où S est le spectre de corps noir émis par les nuages. La température de brillance (correspondant à l'émission thermique) de la face nuit de Vénus est donc de 230 K, dans la plus grande partie du spectre.
-
Question 2
Solution :
La température très élevée de la surface résulte de la très grande épaisseur optique de l'atmosphère en infrarouge. Celle-ci bloque le rayonnement sortant, et empêche le refroidissement de la surface et des basses couches atmosphériques. Cette opacité est due essentiellement à la diffusion par les goutelettes d'acide sulfurique contenues dans les nuages de haute altitude, et dans une moindre mesure au gaz carbonique et à la vapeur d'eau contenus dans l'atmosphère très dense. Vénus présente un exemple extrême d'effet de serre.
-
Question 3
Solution :
Dans ce cas, il faut résoudre l'équation différentielle avec second membre. En faisant l'hypothèse que le seul terme de source non-négligeable est le corps noir de la surface, on trouve :
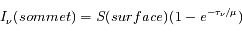
Cette dernière hypothèse est un peu forte, il faudrait en fait tenir compte de l'émisson thermique à toutes les altitudes : la température et l'opacité varient avec l'altitude, et chaque couche de l'atmosphère contribue avec une température différente, qui est atténuée par toute la colonne d'atmosphère au-dessus de cette altitude.
-
Question 4
Solution :
La courbe de corps noir à 233 K ajuste bien la montée de l'intensité à grandes longueurs d'onde, et correspond à l'émission thermique des nuages. Les minima à 4.3 et 4.8 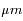 sont des bandes d'absorption du
sont des bandes d'absorption du 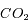 situé au-dessus des nuages. Les maxima à courtes longueurs d'onde sont des fenêtres moins opaques où le rayonnement du bas de l'atmosphère remonte jusqu'au sommet ; on voit dans ces fenêtres un corps noir beaucoup plus chaud.
situé au-dessus des nuages. Les maxima à courtes longueurs d'onde sont des fenêtres moins opaques où le rayonnement du bas de l'atmosphère remonte jusqu'au sommet ; on voit dans ces fenêtres un corps noir beaucoup plus chaud.
Le flux mesuré est donc beaucoup plus élevé dans les régions optiquement minces. Dans les trois bandes situées autour de 1 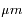 , les photons émis par la surface peuvent remonter jusqu'au sommet de l'atmosphère. Les bandes à 1.75 et 2.3
, les photons émis par la surface peuvent remonter jusqu'au sommet de l'atmosphère. Les bandes à 1.75 et 2.3 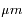 sont trop opaques pour laisser voir la surface, mais des photons émis dans la basse atmosphère peuvent néanmoins s'échapper au-dessus des nuages. Ils sont responsables des pics d'intensité observés à ces longueurs d'onde.
sont trop opaques pour laisser voir la surface, mais des photons émis dans la basse atmosphère peuvent néanmoins s'échapper au-dessus des nuages. Ils sont responsables des pics d'intensité observés à ces longueurs d'onde.
pages_ed-01/exo-eq-kepler.html
Exercice
'équation de Kepler'
-
Question 1
Solution :
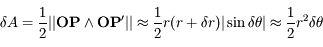 .
.
-
Question 2
Aide :
On rappelle que l'aire totale d'une ellipse est donnée par 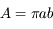 , où
, où 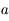 est le demi-grand axe de l'ellipse et
est le demi-grand axe de l'ellipse et 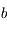 le demi-petit axe donné par
le demi-petit axe donné par 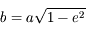 où
où 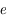 est l'excentricité de l'ellipse.
est l'excentricité de l'ellipse.
Solution :
En passant à la limite dans l'expression précédente on a: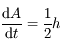 . Or l'aire balayée pendant une période
. Or l'aire balayée pendant une période 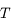 n'est rien d'autre que l'aire totale de l'ellipse. Ainsi, on a:
n'est rien d'autre que l'aire totale de l'ellipse. Ainsi, on a:
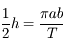 où
où 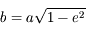 est le demi-petit axe de l'ellipse. Avec
est le demi-petit axe de l'ellipse. Avec 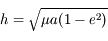 ,
on obtient
,
on obtient 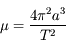 , ce qui correspond bien à la relation demandée.
, ce qui correspond bien à la relation demandée.
-
Question 3
Solution :
Comme 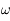 est constant, on a
est constant, on a 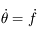 . Ainsi
. Ainsi 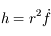 . La solution des équations du mouvement peut aussi s'écrire:
. La solution des équations du mouvement peut aussi s'écrire:
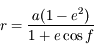 ,
,
Ainsi:
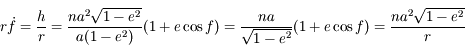 .
.
De même en différentiant l'équation précédente obtenue pour 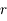 on obtient:
on obtient:
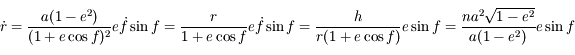 .
.
Ce qui correspond bien à l'équation demandée.
-
Question 4
Solution :
On calcule d'abord 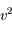 :
:
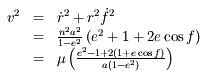 ,
,
qui correspond bien à la relation demandée.
On obtient facilement 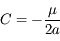 en subsituant
en subsituant 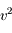 par l'expression ci-dessus dans
par l'expression ci-dessus dans 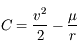 .
.
-
Question 5
Solution :
On a facilement 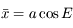 et d'après l'équation de l'ellipse on en déduit
et d'après l'équation de l'ellipse on en déduit 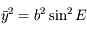 . Comme
. Comme 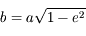 , on en déduit que
, on en déduit que 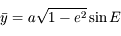 .
.
Ainsi, dans un repère centré sur  avec les mêmes axes on a:
avec les mêmes axes on a: 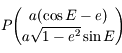 .
.
On en déduit : 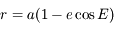 .
.
-
Question 6
Solution :
On a:
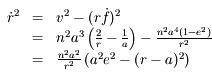 ,
,
ce qui correspond bien à l'équation demandée.
-
Question 7
Aide :
On part de 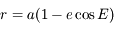 , et on utilise la relation
, et on utilise la relation 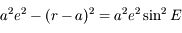 .
.
Solution :
On a vu que 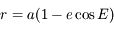 , ainsi
, ainsi 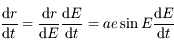 .
.
D'autre part:
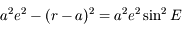 ,
,
Ainsi, on a bien l'équation demandée pour 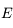 .
.
-
Question 8
Solution :
L'équation différentielle obtenue pour 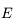 s'écirt:
s'écirt: 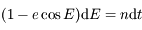 . En intégrant entre l'instant où
. En intégrant entre l'instant où 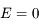 et
et 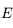 ,on obtient
,on obtient 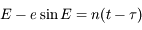 qui correspond bien à l'équation de Kepler.
qui correspond bien à l'équation de Kepler.
pages_ed-02/exo-eqmathieu.html
Exercice
-
Question 1
Solution :
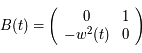 où
où 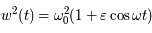 (qui est positive pour
(qui est positive pour  assez petit)
assez petit)
-
Question 2
Solution :
Soit 2 réels 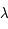 et
et 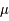 et soit 2 conditions initiales
et soit 2 conditions initiales 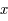 et
et 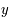 (de
(de 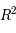 ). L'équation différentielle est linéaire donc
). L'équation différentielle est linéaire donc 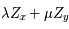 est bien UNE solution de celle-ci.
est bien UNE solution de celle-ci.
Par ailleurs,
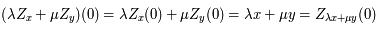
Ainsi on a bien 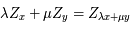
-
Question 3
Solution :
L'équation différentielle (du second ordre) à considérer est:
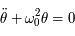
La solution générale est donc
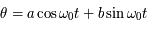
et donc:
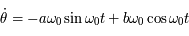
 et
et 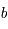 sont des constantes arbitraires que l'on va déterminer pour chacun des vecteur de la base canonique.
sont des constantes arbitraires que l'on va déterminer pour chacun des vecteur de la base canonique.
La première colonne de 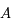 correspond à la solution de condition initiale
correspond à la solution de condition initiale 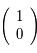 dans la notation matricielle:
dans la notation matricielle:
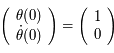
Ce qui donne 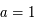 et
et 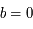 . Soit
. Soit 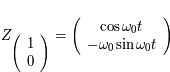
La deuxième colonne de  correspond à la solution de condition initiale
correspond à la solution de condition initiale 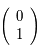 dans la notation matricielle:
dans la notation matricielle:
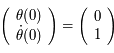
Ce qui donne 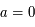 et
et 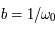 . Soit
. Soit 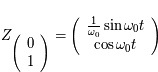
Ainsi 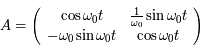
-
Question 4
Solution :
Comme 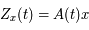 , en
, en  on a:
on a: 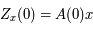 . Or, par définition,
. Or, par définition, 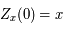 . Ainsi,
. Ainsi, 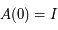 .
.
Par ailleurs, en remplaçant 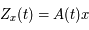 dans l'équation de Mathieu (notée matriciellement), on a:
dans l'équation de Mathieu (notée matriciellement), on a:
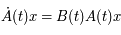
Comme cela est vrai pour tout 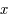 de
de 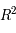 , on a bien
, on a bien 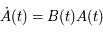 .
.
-
Question 5
Solution :
Pour un déterminant d'ordre 2, un développement direct est facile et suffit à la démonstration.
Développons 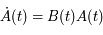 :
:
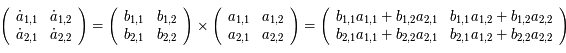
Posons 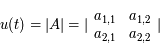 , on a:
, on a:
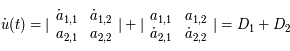
Or
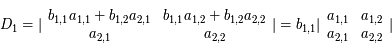
De même
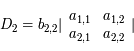
On a ainsi: 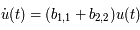 qu'il reste à intégrer. CQFD.
qu'il reste à intégrer. CQFD.
-
Question 6
Solution :
On pose encore 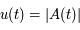 . On a:
. On a:
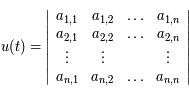
Par la forme mutilinéaire du déterminant, on 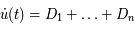 , avec
, avec
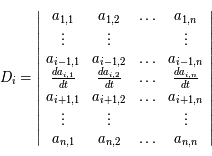
On "développe" 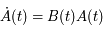 , soit:
, soit:
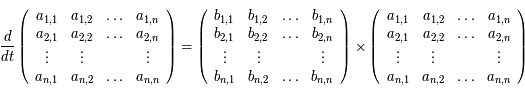
Ainsi la ligne 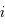 de
de 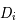 est :
est :
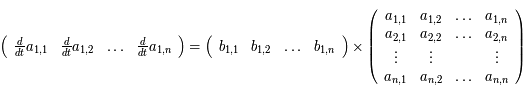
Cette ligne est donc une combinaison linéaire des lignes de 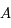 . Or dans un déterminant, on peut remplacer une ligne par cette même ligne à laquelle on ajoute une combinaison linéaire des autres lignes. On a ainsi:
. Or dans un déterminant, on peut remplacer une ligne par cette même ligne à laquelle on ajoute une combinaison linéaire des autres lignes. On a ainsi:
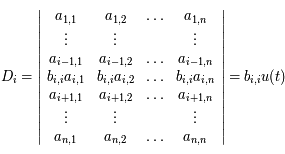
Ainsi, on a bien : 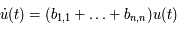
-
Question 7
Solution :
En multipliant à droite chaque membre de la relation 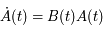 par
par 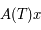 , on obtient
, on obtient
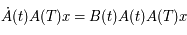
Donc 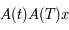 est solution de l'équation de Mathieu (sous forme matricielle:
est solution de l'équation de Mathieu (sous forme matricielle: 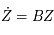 ) de condition initiale
) de condition initiale 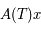 .
.
Il reste à montrer que 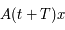 est solution aussi (avec la même condition initiale
est solution aussi (avec la même condition initiale 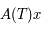 ).
).
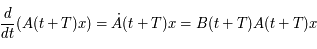
car 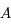 est solution de
est solution de 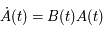 . De plus la matrice
. De plus la matrice 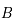 est périodique de période
est périodique de période 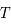 . On a finalement:
. On a finalement:
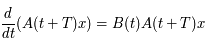
-
Question 8
Solution :
On a 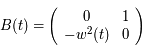 . Donc
. Donc 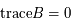 et
et 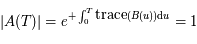
-
Question 9
Solution :
Dans ce cas, 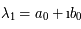 et
et 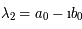 . Elles sont conjuguées car la matrice est réelle. De plus,
. Elles sont conjuguées car la matrice est réelle. De plus, 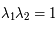 , donc
, donc 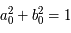 . C'est donc une matrice de rotation. Or
. C'est donc une matrice de rotation. Or 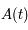 est borné sur l'intervalle borné
est borné sur l'intervalle borné 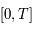 . Par la relation
. Par la relation 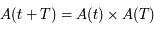 , on en déduit que
, on en déduit que 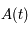 est borné sur l'ensemble des réels.
est borné sur l'ensemble des réels.
-
Question 10
Solution :
Le polynôme caractéristique est
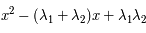
soit
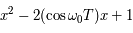
Le discrimant réduit est 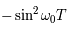 . La seule manière d'éviter des valeurs propres complexes est donc que le discriminant soit nul.
. La seule manière d'éviter des valeurs propres complexes est donc que le discriminant soit nul.
pages_ed-02/exo-ed-02.html
Exercice
'Détermination du potentiel dans une sphère de Debye'
-
Question 1
Solution :
1)
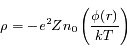
En coordonnée sphérique:
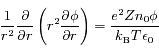
Soit 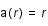 ,
, 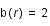 ,
, 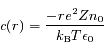 .
.
2)
On pose 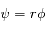 et donc
et donc 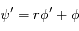 et
et 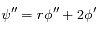
Il vient 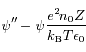
3)
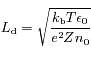
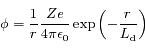
pages_ed-02/exo-pb-22-corps.html
Exercice
' Le problème de 2 corps'
pages_ed-02/exo-train-gravitationnel.html
Exercice
'Train gravitationnel'
-
Question 1
Solution :
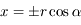
-
Question 2
Solution :
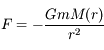 , où
, où 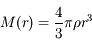 est la masse contenue à l'intérieur de la sphère de rayon
est la masse contenue à l'intérieur de la sphère de rayon 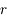 .
.
Donc 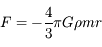 .
.
-
Question 3
Solution :
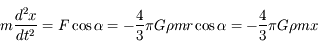 .
.
On reconnaît l'équation d'un pendule de pulsation 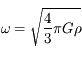 .
.
-
Question 4
Solution :
Le train peut donc atteindre le point B, la solution est périodique de période 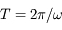 .
.
La durée du trajet est 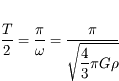 = 42 min 14 s, quels que soient les points A et B.
= 42 min 14 s, quels que soient les points A et B.
pages_ed-02/exo-pendule-foucault.html
Exercice
'Pendule de Foucault'
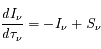
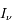 est l'intensité lumineuse à la fréquence
est l'intensité lumineuse à la fréquence 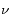 ,
, 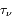 est la profondeur optique du milieu,
est la profondeur optique du milieu, 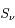 est la fonction source, égale au rapport du coefficient d'émission au coefficient d'absorption du milieu traversé.
est la fonction source, égale au rapport du coefficient d'émission au coefficient d'absorption du milieu traversé.
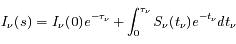
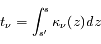 est l'épaisseur optique entre les points s' et s, et
est l'épaisseur optique entre les points s' et s, et 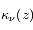 est le coefficient d'absorption du milieu en z.
est le coefficient d'absorption du milieu en z.



 où l'atmosphère n'est pas entièrement opaque. Ecrire le flux émergent dans ces régions spectrales où l'atmosphère est semi-transparente.
où l'atmosphère n'est pas entièrement opaque. Ecrire le flux émergent dans ces régions spectrales où l'atmosphère est semi-transparente.


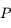 de masse négligeable soumise à l'attraction universelle d'un corps de masse
de masse négligeable soumise à l'attraction universelle d'un corps de masse 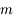 situé au centre
situé au centre 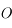 du repère de référence. La force s'appliquant à
du repère de référence. La force s'appliquant à 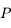 est donnée par :
est donnée par : 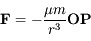 , où la notation en gras dénote des vecteurs,
, où la notation en gras dénote des vecteurs, 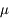 est la constante universelle de la gravitation, et
est la constante universelle de la gravitation, et 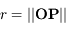 . Les coordonnées de
. Les coordonnées de 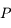 dans le repère tournant étant
dans le repère tournant étant 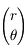 , on a vu dans l'exercice du
, on a vu dans l'exercice du 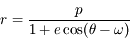 ,
,
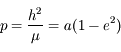 ,
, 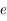 est l'
est l'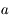 est le
est le 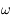 est l'
est l'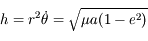 est une constante du mouvement, ainsi que l'intégrale de l'énergie donnée par
est une constante du mouvement, ainsi que l'intégrale de l'énergie donnée par 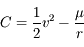 , où
, où 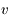 est la norme de la vitesse de
est la norme de la vitesse de  .
.
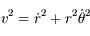 .
.
 et l'instant
et l'instant 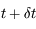 , le point
, le point 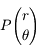 s'est déplacé au point
s'est déplacé au point 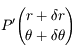 . En déduire, l'aire élémentaire
. En déduire, l'aire élémentaire 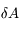 balayée par le rayon vecteur
balayée par le rayon vecteur  pendant l'intervalle de temps
pendant l'intervalle de temps 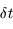 . On ne retiendra que les quantités d'ordre 1.
. On ne retiendra que les quantités d'ordre 1.
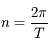 , où
, où 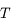 est la période du mouvement est tel que
est la période du mouvement est tel que 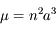 .
.
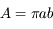 , où
, où 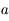 est le demi-grand axe de l'ellipse et
est le demi-grand axe de l'ellipse et 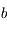 le demi-petit axe donné par
le demi-petit axe donné par 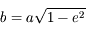 où
où 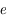 est l'excentricité de l'ellipse.
est l'excentricité de l'ellipse.
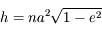 , montrer que:
, montrer que:
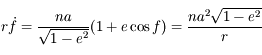
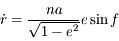
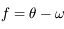 .
. 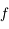 s'appelle l'
s'appelle l'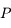 vu depuis le foyer
vu depuis le foyer 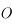 .
.
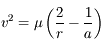 , en déduire que l'intégrale de l'énergie
, en déduire que l'intégrale de l'énergie 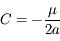 .
.
 le cercle de centre le centre
le cercle de centre le centre  de l'ellipse correspondant à la trajectoire de
de l'ellipse correspondant à la trajectoire de 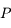 et de diamètre le grand axe de l'ellipse, c'est à dire
et de diamètre le grand axe de l'ellipse, c'est à dire 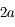 . La projection de
. La projection de 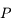 sur le cercle
sur le cercle 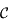 parallèlement au petit axe de l'ellipse est noté
parallèlement au petit axe de l'ellipse est noté 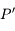 . On appelle
. On appelle 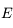 entre
entre 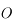 et
et 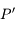 vu depuis
vu depuis 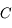 . Sachant que l'équation de l'ellipse correspondant à la trajectoire de
. Sachant que l'équation de l'ellipse correspondant à la trajectoire de 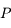 dans le repère centré sur
dans le repère centré sur 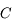 et d'axe des abscisses le grand axe dirigé vers le foyer
et d'axe des abscisses le grand axe dirigé vers le foyer 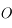 , et d'axe des ordonnées la direction orthogonale dans le sens direct, est:
, et d'axe des ordonnées la direction orthogonale dans le sens direct, est:
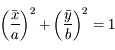 ,
,
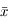 et
et 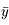 en fonction de
en fonction de 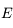 , puis l'expression de
, puis l'expression de 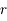 en fonction de
en fonction de 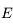 .
.
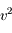 que
que 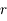 vérifie l'équation différentielle suivante:
vérifie l'équation différentielle suivante:
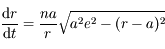
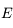 vérifie l'équation différentielle:
vérifie l'équation différentielle:
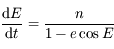 .
.
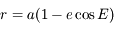 , et on utilise la relation
, et on utilise la relation 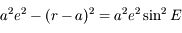 .
.
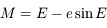 , où l'
, où l'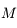 est définie par
est définie par 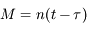 où
où 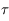 correspond à l'instant de passage au péricentre, c'est à dire quand
correspond à l'instant de passage au péricentre, c'est à dire quand  .
.
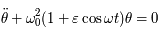
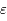 est nul, c'est l'équation d'un pendule simple pour de petites oscillations. Dans ce cas,
est nul, c'est l'équation d'un pendule simple pour de petites oscillations. Dans ce cas, 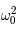 est inversement proportionnel à la longueur du pendule. On rappelle que la période
est inversement proportionnel à la longueur du pendule. On rappelle que la période 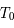 est alors
est alors 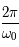 .
.
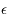 est un petit paramètre. On dit que le modèle du pendule simple est perturbé. L'équation de Mathieu est un cas particulier de l'équation
est un petit paramètre. On dit que le modèle du pendule simple est perturbé. L'équation de Mathieu est un cas particulier de l'équation
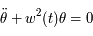
 est une fonction périodique de période
est une fonction périodique de période  qui est utilisée en Mécanique Céleste pour l'étude du mouvement de la Lune.
qui est utilisée en Mécanique Céleste pour l'étude du mouvement de la Lune.
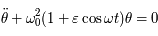
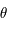 est une fonction du temps
est une fonction du temps  . Cette équation dépend des paramètres
. Cette équation dépend des paramètres 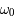 ,
, 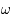 et
et 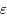 .
.
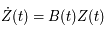
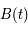 est une matrice
est une matrice 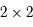 réelle. Donner la signification de la nouvelle inconnue
réelle. Donner la signification de la nouvelle inconnue 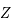 (par rapport à
(par rapport à 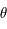 ).
).
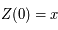 (on a
(on a 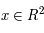 ). D'après le théorème de Cauchy l'équation différentielle a alors une solution unique que l'on note
). D'après le théorème de Cauchy l'équation différentielle a alors une solution unique que l'on note 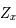
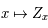 est linéaire.
est linéaire.
 donné, cette application va de
donné, cette application va de 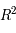 dans
dans 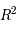 . Il existe donc une matrice
. Il existe donc une matrice 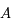 de
de 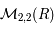 telle que
telle que 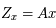 ou encore
ou encore 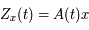 . Explciter la matrice
. Explciter la matrice 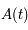 seulement dans le cas
seulement dans le cas 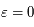 .
.
 , revient à obtenir toutes les solutions de l'équation différentielle.
, revient à obtenir toutes les solutions de l'équation différentielle.  est donc une inconnue. Montrer que
est donc une inconnue. Montrer que  vérifie le système suivant:
vérifie le système suivant:
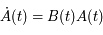
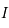 est la matrice identité.
est la matrice identité.
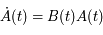
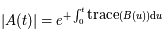
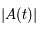 est le déterminant (d'ordre 2) de
est le déterminant (d'ordre 2) de 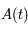 et
et 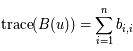 (somme des éléments diagonaux).
(somme des éléments diagonaux).
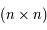 . C'est-à-dire pour
. C'est-à-dire pour 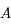 et
et 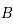 étant des matrices
étant des matrices 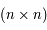 .
.
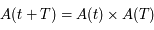
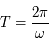
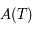 s'appelle la matrice de Floquet.
s'appelle la matrice de Floquet.
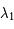 et
et 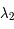 de la matrice de Floquet vérifient:
de la matrice de Floquet vérifient:
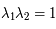
 . Donc avec
. Donc avec 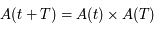 et une condition initale prise dans la direction du vecteur propre associé à cette valeur propre, la solution tendera vers l'infini.
et une condition initale prise dans la direction du vecteur propre associé à cette valeur propre, la solution tendera vers l'infini.
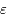 est petit. On peut alors montrer que la somme des valeurs propres de
est petit. On peut alors montrer que la somme des valeurs propres de 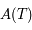 est la trace de la matrice
est la trace de la matrice 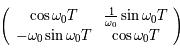 (ie: correspondant à celle trouvée dans le cas de perturbation nulle). Donc
(ie: correspondant à celle trouvée dans le cas de perturbation nulle). Donc
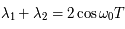
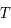 du forçage est telle que
du forçage est telle que
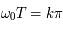
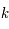 est un entier relatif.
est un entier relatif.
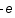 et d'ions de charge
et d'ions de charge 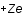 .
.
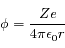 où
où 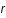 est la distance à l'ion. Ce potentiel est appelé le potentiel Coulombien.
est la distance à l'ion. Ce potentiel est appelé le potentiel Coulombien.
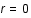 et soit
et soit 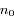 la densité ionique moyenne dans le plasma. Si le plasma est suffisamment chaud, on peut montrer que la densité électronique est égal à
la densité ionique moyenne dans le plasma. Si le plasma est suffisamment chaud, on peut montrer que la densité électronique est égal à
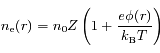
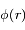 est le potentiel en
est le potentiel en 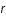 ,
, 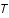 la température du plasma et
la température du plasma et 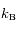 la constante de Boltzmann.
la constante de Boltzmann.
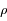 et le potentiel
et le potentiel 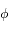 de la manière suivante:
de la manière suivante:
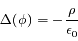
 sous la forme
sous la forme 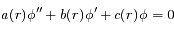
 tel que l'équation différentielle du second ordre vérifiée par
tel que l'équation différentielle du second ordre vérifiée par 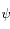 soit à coefficients constants.
soit à coefficients constants.
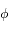 . Les conditions aux limites sont que le potentiel
. Les conditions aux limites sont que le potentiel 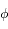 doit tendre vers 0 lorsque
doit tendre vers 0 lorsque 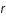 tend vers l'infini et il doit être équivalent au potentiel Coulombien lorsque
tend vers l'infini et il doit être équivalent au potentiel Coulombien lorsque 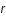 tend vers 0. En déduire la distance caractéristique d'écrantage de la charge centrale (longueur de Debye) dans ce cas.
tend vers 0. En déduire la distance caractéristique d'écrantage de la charge centrale (longueur de Debye) dans ce cas.
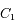 et
et 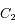 de masses respectives
de masses respectives 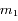 et
et 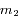 , isolés de toute autre influence, alors l'équation du mouvement de
, isolés de toute autre influence, alors l'équation du mouvement de 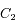 par rapport à
par rapport à 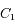 est:
est:
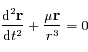
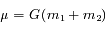 avec
avec 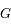 la constante universelle de la gravitation, et
la constante universelle de la gravitation, et 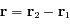 avec
avec 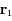 et
et 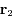 désignant les vecteurs positions des corps
désignant les vecteurs positions des corps 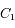 et
et 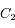 dans un repère inertiel.
dans un repère inertiel.
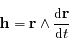 est une constante du mouvement. Cette constante s'appelle l'intégrale du moment angulaire.
est une constante du mouvement. Cette constante s'appelle l'intégrale du moment angulaire.
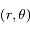 où
où 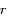 est la norme de
est la norme de 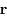 et
et 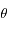 est l'angle en radian entre une direction fixe et
est l'angle en radian entre une direction fixe et 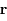 compté positivement dans le sens trigonométrique, montrer que la norme du moment angulaire s'écrit
compté positivement dans le sens trigonométrique, montrer que la norme du moment angulaire s'écrit 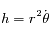 , où le point
, où le point 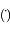 désigne la première dérivée par rapport au temps. Cette équation correspond à la deuxième loi de Kepler.
désigne la première dérivée par rapport au temps. Cette équation correspond à la deuxième loi de Kepler.
 (qui n'est rien d'autre que le vecteur vitesse), montrer que
(qui n'est rien d'autre que le vecteur vitesse), montrer que
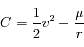 est une constante du mouvement (
est une constante du mouvement (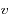 désignant la norme du vecteur vitesse).
désignant la norme du vecteur vitesse). 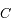 s'appelle l'intégrale de l'énergie.
s'appelle l'intégrale de l'énergie.
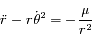
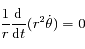
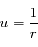 , exprimer
, exprimer 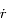 et
et 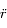 en fonction de
en fonction de 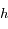 ,
, 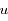 , et les dérivées première et seconde de
, et les dérivées première et seconde de 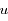 par rapport à
par rapport à 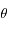 que l'on notera
que l'on notera 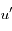 et
et 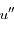 .
.
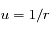 dans l'équation différentielle du second ordre obtenue pour
dans l'équation différentielle du second ordre obtenue pour 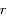 , écrire une équation linéaire du second ordre pour
, écrire une équation linéaire du second ordre pour 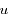 en considérant
en considérant 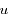 comme une fonction de
comme une fonction de 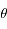 .
.
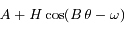 où
où 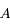 et
et 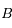 sont des constantes que l'on déterminera et
sont des constantes que l'on déterminera et 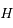 et
et 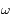 des constantes d'intégrations.
des constantes d'intégrations.
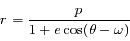 avec
avec 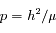 ,
, 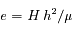 et
et 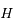 et
et 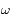 sont deux constantes d'intégration.
sont deux constantes d'intégration.
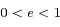 , on pourrait montrer que dans ce cas la solution correspond à une ellipse d'excentricité
, on pourrait montrer que dans ce cas la solution correspond à une ellipse d'excentricité  et de demi-grand axe
et de demi-grand axe 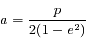 mais ceci fait l'objet d'un autre exercice.
mais ceci fait l'objet d'un autre exercice.
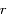 sont
sont 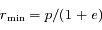 et
et 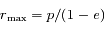 et sont obtenues pour
et sont obtenues pour 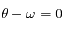 et
et 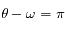 respectivement. Ces positions sont appelées péricentre et apocentre respectivement. Elles sont à l'oposées l'une de l'autre,
respectivement. Ces positions sont appelées péricentre et apocentre respectivement. Elles sont à l'oposées l'une de l'autre, 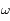 donnant la direction du pericentre et
donnant la direction du pericentre et 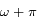 celle de l'apocentre.
La distance séparant ces deux positions est donc
celle de l'apocentre.
La distance séparant ces deux positions est donc 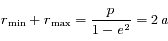 , où
, où 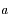 est ce qu'on appelle le demi-grand axe.
est ce qu'on appelle le demi-grand axe.
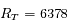 km et de masse volumique uniforme
km et de masse volumique uniforme 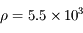
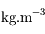 . Soit
. Soit 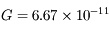 S.I. la contante de gravitation universelle. On imagine un tunnel rectiligne entre 2 points A et B quelconques de la surface terrestre, et un train roulant sans frottement dans ce tunnel. Partant de A sous l'action de la pesanteur, le wagon va accélérer jusqu'au milieu du tunnel, puis décélérer une fois atteinte la distance de moindre approche du centre 0 de la Terre (voir figure). Le train atteindra-t-il le point B, et si oui, en combien de temps?
S.I. la contante de gravitation universelle. On imagine un tunnel rectiligne entre 2 points A et B quelconques de la surface terrestre, et un train roulant sans frottement dans ce tunnel. Partant de A sous l'action de la pesanteur, le wagon va accélérer jusqu'au milieu du tunnel, puis décélérer une fois atteinte la distance de moindre approche du centre 0 de la Terre (voir figure). Le train atteindra-t-il le point B, et si oui, en combien de temps?

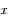 , sa distance au centre de la Terre est notée
, sa distance au centre de la Terre est notée 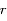 .
.
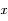 la distance du train au milieu du tunnel. Exprimer
la distance du train au milieu du tunnel. Exprimer 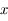 en fonction de la distance au centre de la Terre
en fonction de la distance au centre de la Terre 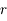 et de l'angle
et de l'angle 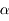 .
.
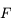 agissant sur le train en fonction de la masse du train
agissant sur le train en fonction de la masse du train 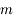 , de la masse volumique de la Terre
, de la masse volumique de la Terre 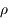 et de la distance au centre de la Terre
et de la distance au centre de la Terre 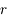 .
.

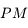 accroché en
accroché en 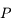 de longueur
de longueur 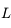 et d'une boule
et d'une boule 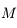 de masse
de masse 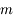 . L'espace est rapporté au système d'axes
. L'espace est rapporté au système d'axes 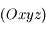 fixe dans le réferentiel lié à la Terre, l'axe
fixe dans le réferentiel lié à la Terre, l'axe 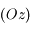 passant par
passant par 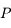 et le centre de la Terre (voir figures).
On se place dans le cas de faibles oscillations. On rappelle que dans ce cas, le mouvement de la boule
et le centre de la Terre (voir figures).
On se place dans le cas de faibles oscillations. On rappelle que dans ce cas, le mouvement de la boule 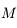 de coordonnées
de coordonnées 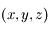 se fait dans le plan
se fait dans le plan 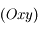 et que le module de la tension du fil
et que le module de la tension du fil 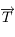 est
est 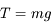 où
où 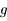 est l'accélération de la pesanteur. On note
est l'accélération de la pesanteur. On note 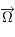 le vecteur rotation de la Terre et
le vecteur rotation de la Terre et 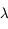 la latitude du lieu.
Le bilan des forces doit faire intervenir la force d'inertie de Coriolis, dont l'expression est
la latitude du lieu.
Le bilan des forces doit faire intervenir la force d'inertie de Coriolis, dont l'expression est 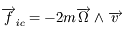 où
où 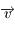 désigne la vitesse dans le repère
désigne la vitesse dans le repère 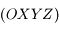 . Par contre, il n'y a pas lieu de tenir compte de la force d'inertie d'entrainement, car celle-ci est déjà incluse dans la définiton de la pesanteur, i.e. dans l'expression de
. Par contre, il n'y a pas lieu de tenir compte de la force d'inertie d'entrainement, car celle-ci est déjà incluse dans la définiton de la pesanteur, i.e. dans l'expression de 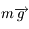 .
Une fois le bilan des forces effectué, on peut montrer que les composantes de la tension du fil dans
.
Une fois le bilan des forces effectué, on peut montrer que les composantes de la tension du fil dans 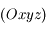 sont
sont 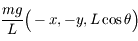 et que les composantes de la force de Coriolis sont
et que les composantes de la force de Coriolis sont 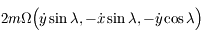 . D'après l'hypothèse faite sur la petitesse des oscillations, il n'y a pas lieu de considérer l'équation obtenue par projection sur
. D'après l'hypothèse faite sur la petitesse des oscillations, il n'y a pas lieu de considérer l'équation obtenue par projection sur 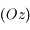 , celle-ci pouvant être considérée comme un terme correctif. On ne considère donc que les projections selon les deux autres directions, et en posant
, celle-ci pouvant être considérée comme un terme correctif. On ne considère donc que les projections selon les deux autres directions, et en posant 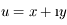 où
où 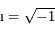 , et en posant aussi
, et en posant aussi 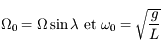 on peut montrer que l'équation du mouvement, complexe, se met sous la forme :
on peut montrer que l'équation du mouvement, complexe, se met sous la forme : 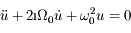 .
.


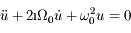
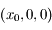 avec une vitesse initiale nulle.
avec une vitesse initiale nulle.
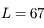 m,
m, 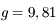 m/s2, et
m/s2, et 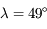 Nord. Justifier que
Nord. Justifier que 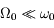 .
.
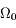 devant
devant 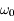 . Interpréter.
. Interpréter.
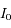 l'intensité reçue au sommet de l'atmosphère (flux solaire).
l'intensité reçue au sommet de l'atmosphère (flux solaire).
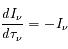 soit :
soit : 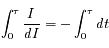
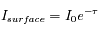
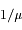 , où
, où 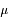 est le cosinus de l'angle d'incidence.
est le cosinus de l'angle d'incidence.
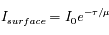
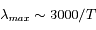 , soit environ 4
, soit environ 4 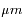 pour la surface, et 12
pour la surface, et 12 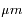 pour les nuages. On pourrait s'attendre à ce que l'émission de surface, beaucoup plus élevée, domine le spectre (voir les propriétés du
pour les nuages. On pourrait s'attendre à ce que l'émission de surface, beaucoup plus élevée, domine le spectre (voir les propriétés du 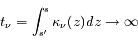 (cas optiquement épais). L'équation de transfert s'écrit dans ce cas :
(cas optiquement épais). L'équation de transfert s'écrit dans ce cas :
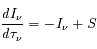 soit
soit 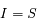 au sommet de l'atmosphère, où S est le spectre de corps noir émis par les nuages. La
au sommet de l'atmosphère, où S est le spectre de corps noir émis par les nuages. La 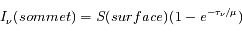
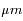 sont des bandes d'absorption du
sont des bandes d'absorption du 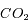 situé au-dessus des nuages. Les maxima à courtes longueurs d'onde sont des fenêtres moins opaques où le rayonnement du bas de l'atmosphère remonte jusqu'au sommet ; on voit dans ces fenêtres un corps noir beaucoup plus chaud.
situé au-dessus des nuages. Les maxima à courtes longueurs d'onde sont des fenêtres moins opaques où le rayonnement du bas de l'atmosphère remonte jusqu'au sommet ; on voit dans ces fenêtres un corps noir beaucoup plus chaud.
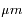 , les photons émis par la surface peuvent remonter jusqu'au sommet de l'atmosphère. Les bandes à 1.75 et 2.3
, les photons émis par la surface peuvent remonter jusqu'au sommet de l'atmosphère. Les bandes à 1.75 et 2.3 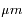 sont trop opaques pour laisser voir la surface, mais des photons émis dans la basse atmosphère peuvent néanmoins s'échapper au-dessus des nuages. Ils sont responsables des pics d'intensité observés à ces longueurs d'onde.
sont trop opaques pour laisser voir la surface, mais des photons émis dans la basse atmosphère peuvent néanmoins s'échapper au-dessus des nuages. Ils sont responsables des pics d'intensité observés à ces longueurs d'onde.
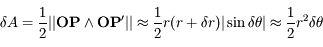 .
.
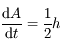 . Or l'aire balayée pendant une période
. Or l'aire balayée pendant une période 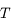 n'est rien d'autre que l'aire totale de l'ellipse. Ainsi, on a:
n'est rien d'autre que l'aire totale de l'ellipse. Ainsi, on a:
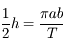 où
où 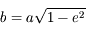 est le demi-petit axe de l'ellipse. Avec
est le demi-petit axe de l'ellipse. Avec 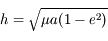 ,
on obtient
,
on obtient 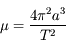 , ce qui correspond bien à la relation demandée.
, ce qui correspond bien à la relation demandée.
 est constant, on a
est constant, on a 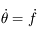 . Ainsi
. Ainsi 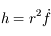 . La solution des équations du mouvement peut aussi s'écrire:
. La solution des équations du mouvement peut aussi s'écrire:
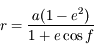 ,
,
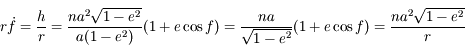 .
.
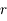 on obtient:
on obtient:
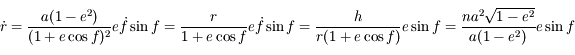 .
.
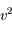 :
:
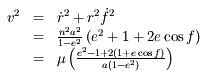 ,
,
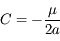 en subsituant
en subsituant 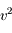 par l'expression ci-dessus dans
par l'expression ci-dessus dans 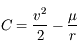 .
.
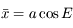 et d'après l'équation de l'ellipse on en déduit
et d'après l'équation de l'ellipse on en déduit 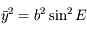 . Comme
. Comme 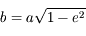 , on en déduit que
, on en déduit que 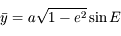 .
.
 avec les mêmes axes on a:
avec les mêmes axes on a: 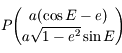 .
.
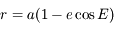 .
.
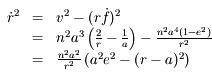 ,
,
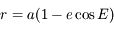 , ainsi
, ainsi 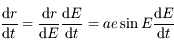 .
.
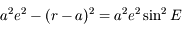 ,
,
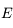 .
.
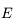 s'écirt:
s'écirt: 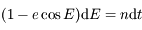 . En intégrant entre l'instant où
. En intégrant entre l'instant où 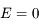 et
et 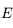 ,on obtient
,on obtient 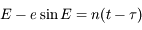 qui correspond bien à l'équation de Kepler.
qui correspond bien à l'équation de Kepler.
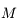 connaissant
connaissant 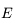 . Malheureusement on a en générale besoin de connaître
. Malheureusement on a en générale besoin de connaître 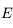 (qui est un angle géométrique relié à la position de l'objet sur son orbite) connaissant
(qui est un angle géométrique relié à la position de l'objet sur son orbite) connaissant 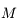 (qui est proportionelle au temps). Pour cela on doit inverser l'équation de Kepler. Cette inversion est l'objet de cet
(qui est proportionelle au temps). Pour cela on doit inverser l'équation de Kepler. Cette inversion est l'objet de cet 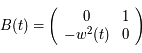 où
où 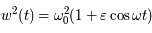 (qui est positive pour
(qui est positive pour  assez petit)
assez petit)
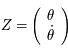
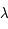 et
et 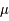 et soit 2 conditions initiales
et soit 2 conditions initiales 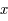 et
et 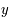 (de
(de 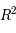 ). L'équation différentielle est linéaire donc
). L'équation différentielle est linéaire donc 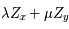 est bien UNE solution de celle-ci.
est bien UNE solution de celle-ci.
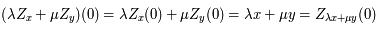
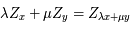
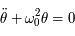
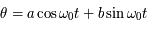
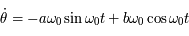
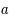 et
et 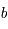 sont des constantes arbitraires que l'on va déterminer pour chacun des vecteur de la base canonique.
sont des constantes arbitraires que l'on va déterminer pour chacun des vecteur de la base canonique.
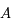 correspond à la solution de condition initiale
correspond à la solution de condition initiale 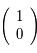 dans la notation matricielle:
dans la notation matricielle:
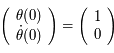
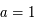 et
et 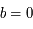 . Soit
. Soit 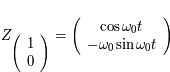
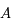 correspond à la solution de condition initiale
correspond à la solution de condition initiale 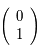 dans la notation matricielle:
dans la notation matricielle:
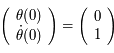
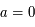 et
et 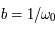 . Soit
. Soit 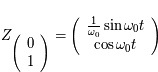
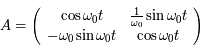
 , en
, en  on a:
on a: 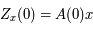 . Or, par définition,
. Or, par définition, 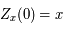 . Ainsi,
. Ainsi, 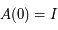 .
.
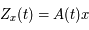 dans l'équation de Mathieu (notée matriciellement), on a:
dans l'équation de Mathieu (notée matriciellement), on a:
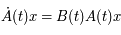
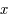 de
de 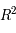 , on a bien
, on a bien 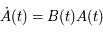 .
.
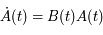 :
:
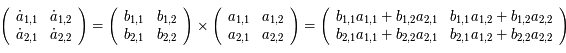
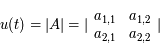 , on a:
, on a:
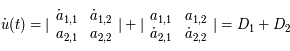
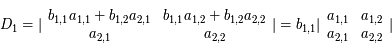
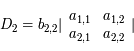
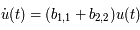 qu'il reste à intégrer. CQFD.
qu'il reste à intégrer. CQFD.
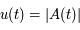 . On a:
. On a:
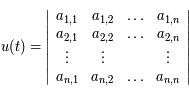
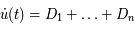 , avec
, avec
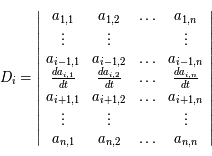
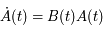 , soit:
, soit:
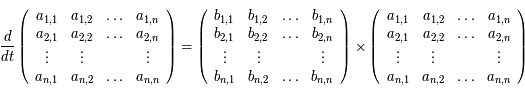
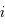 de
de 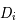 est :
est :
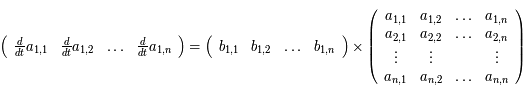
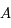 . Or dans un déterminant, on peut remplacer une ligne par cette même ligne à laquelle on ajoute une combinaison linéaire des autres lignes. On a ainsi:
. Or dans un déterminant, on peut remplacer une ligne par cette même ligne à laquelle on ajoute une combinaison linéaire des autres lignes. On a ainsi:
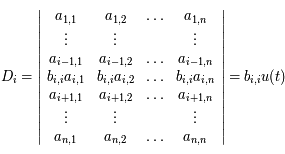
 par
par 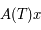 , on obtient
, on obtient
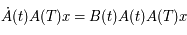
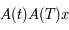 est solution de l'équation de Mathieu (sous forme matricielle:
est solution de l'équation de Mathieu (sous forme matricielle: 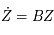 ) de condition initiale
) de condition initiale 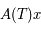 .
.
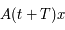 est solution aussi (avec la même condition initiale
est solution aussi (avec la même condition initiale 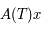 ).
).
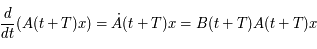
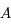 est solution de
est solution de 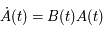 . De plus la matrice
. De plus la matrice 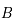 est périodique de période
est périodique de période 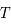 . On a finalement:
. On a finalement:
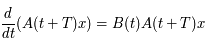
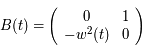 . Donc
. Donc 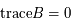 et
et 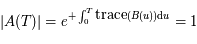
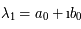 et
et 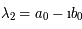 . Elles sont conjuguées car la matrice est réelle. De plus,
. Elles sont conjuguées car la matrice est réelle. De plus, 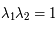 , donc
, donc 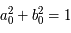 . C'est donc une matrice de rotation. Or
. C'est donc une matrice de rotation. Or 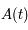 est borné sur l'intervalle borné
est borné sur l'intervalle borné 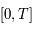 . Par la relation
. Par la relation 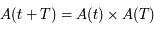 , on en déduit que
, on en déduit que 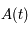 est borné sur l'ensemble des réels.
est borné sur l'ensemble des réels.
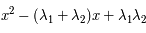
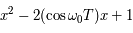
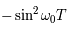 . La seule manière d'éviter des valeurs propres complexes est donc que le discriminant soit nul.
. La seule manière d'éviter des valeurs propres complexes est donc que le discriminant soit nul.
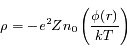
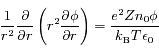
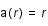 ,
, 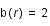 ,
, 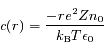 .
.
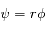 et donc
et donc 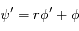 et
et 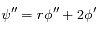
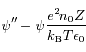
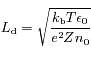
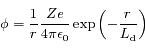
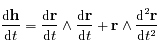 or
or 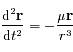 et le produit vectoriel de deux vecteurs colinéaires est nul donc
et le produit vectoriel de deux vecteurs colinéaires est nul donc
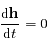 .
.
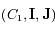 un repère orthonormal direct du plan tel que les angles sont mesurés à partir du vecteur
un repère orthonormal direct du plan tel que les angles sont mesurés à partir du vecteur 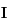 . Dans ce repère on a
. Dans ce repère on a 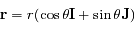 et
et 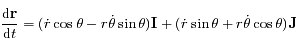 .
Ainsi, sachant que
.
Ainsi, sachant que 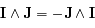 et que
et que 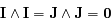 on a
on a 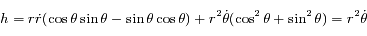 .
.
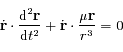 .
.
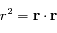 et
et 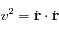 , on remarque que :
, on remarque que :
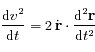 et
et 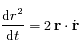 .
.
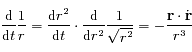
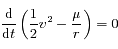 ,
,
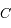 est bien une constante du mouvement.
est bien une constante du mouvement.
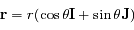 et
et 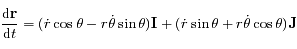 .
.
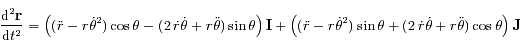 .
.
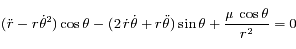
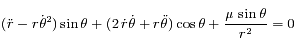
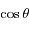 et la deuxième par
et la deuxième par 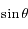 et en sommant les deux équations obtenues d'une part ; et en multipliant la première équation par
et en sommant les deux équations obtenues d'une part ; et en multipliant la première équation par 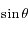 et la deuxième par
et la deuxième par 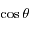 et en soustrayant les deux équations obtenues d'autre part ; on obtient le système suivant:
et en soustrayant les deux équations obtenues d'autre part ; on obtient le système suivant:
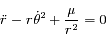
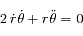
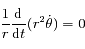 .
.
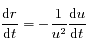 or l'intégrale du moment angulaire implique que
or l'intégrale du moment angulaire implique que 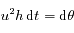 , ainsi
, ainsi 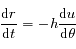 ;
que l'on peut aussi noter
;
que l'on peut aussi noter 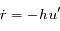 .
De même
.
De même 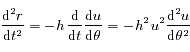 , que l'on peut écrire
, que l'on peut écrire 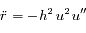
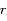 devient:
devient:
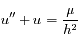
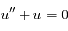 . Le polynôme caractéristique de l'équation est
. Le polynôme caractéristique de l'équation est 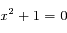 , qui a deux solutions complexes conjuguées
, qui a deux solutions complexes conjuguées  et
et 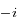 (où
(où  est tel que
est tel que 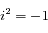 ). Ainsi la solution générale de l'équation sans second membre s'écrit:
). Ainsi la solution générale de l'équation sans second membre s'écrit:
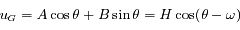
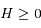 et
et 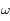 sont des constantes du mouvement dépendant des conditions initiales.
sont des constantes du mouvement dépendant des conditions initiales.
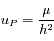 .
On en déduit la solution générale de notre équation:
.
On en déduit la solution générale de notre équation:
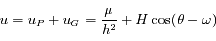
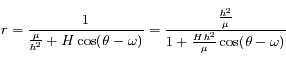
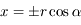
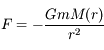 , où
, où 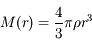 est la masse contenue à l'intérieur de la sphère de rayon
est la masse contenue à l'intérieur de la sphère de rayon 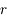 .
.
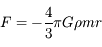 .
.
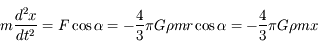 .
.
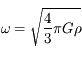 .
.
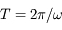 .
.
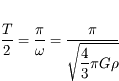 = 42 min 14 s, quels que soient les points A et B.
= 42 min 14 s, quels que soient les points A et B.
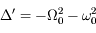
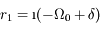 et
et 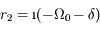 où
où 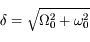 . La solution générale de l'équation différentielle est donc
. La solution générale de l'équation différentielle est donc 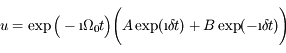
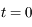 on a
on a 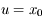 . De plus
. De plus 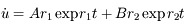 . On en déduit, la vitesse initiale étant nulle, que
. On en déduit, la vitesse initiale étant nulle, que 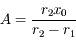 et
et 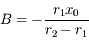 . Donc
. Donc 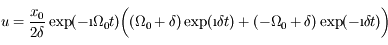
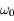 et à
et à 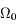 sont de 16,4 s et 31h40min.
sont de 16,4 s et 31h40min.
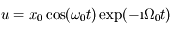
 dont le plan d'oscillation tourne avec la fréquence
dont le plan d'oscillation tourne avec la fréquence 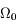 .
.