Fonction d'une variable réelle : dérivabilité
- Introduction
- Définition
- Rétrogradation de Mars
- Ex : rétrogradation de Mars
- Orbites perturbées du problème à 2 corps
- Ex: Orbites perturbées du problème à 2 corps
- Loi de Planck en fréquence
- Ex: loi de Planck en fréquence
- Théorème des accroissements finis
- Les racines du polynôme de la méthode de Laplace
- Ex: Les racines du polynôme de la méthode de Laplace
- Les racines des polynômes de Legendre
- Ex: Les racines des polynômes de Legendre
- Projection de Mollweide
- Ex : projection de Mollweide
- Extrema
- Loi de Wien
- Ex : loi de Wien
- Etoile à neutron
- Ex: Etoile à neutron
- Sphère photonique
- Ex: Sphère photonique
Introduction
On trouvera dans cette partie les exercices suivants :
- étude de la rétrogradation de la planète Mars
- perturbation d'une orbite elliptique
- loi de Planck en fréquence
- étude des racines réelles du polynôme de degré 8 issu de la méthode de Laplace (détermination d'orbite)
- le théorème de Rolle appliquée dans une récurrence pour les racines des polynômes de Legendre
- étude de la projection cartographique de Mollweide
- démonstration de la loi du déplacement de Wien pour le corps noir (application de la détermination d'un extrema pour une fonction continue sur un intervalle fermé)
- rayon d'équilibre d'une étoile à Neutron (application de la détermination d'un extrema pour une fonction continue sur un intervalle fermé)
- calcul de la sphère de photons d'un trou noir
Définition
Auteurs: Marc Fouchard, S. Renner, Stéphane Erard
Rétrogradation de Mars
Auteur : Marc Fouchard
Le mouvement de Mars vu depuis la Terre montre des périodes pendant lesquelles Mars se déplace dans le sens inverse au
Soleil par rapport au fond d'étoiles fixes. L'exercice présenté ici consiste à étudier cette phase de rétrogradation de Mars.
L'animation ci-dessous montre à gauche le mouvement de la Terre et de Mars autour du Soleil et à droite les mêmes mouvements vus depuis la Terre.
Retrogradation de Mars
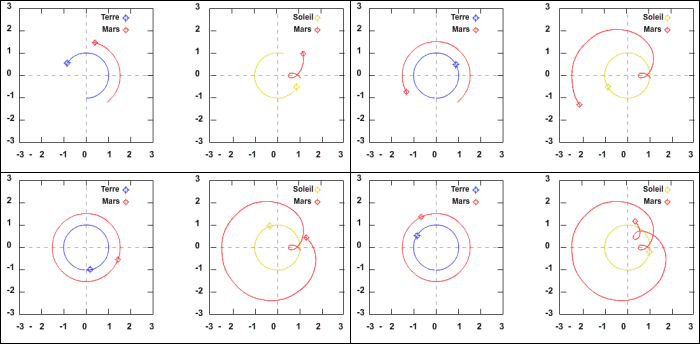
Mouvement de la Terre et de Mars autour du Soleil.
On remarque que vu de la Terre le mouvement de Mars se fait dans le sens inverse (sens retrograde) à celui du Soleil (sens prograde). Le but de cet exercice est d'étudier cette phase de rétrogradation.
Ex : rétrogradation de Mars
Orbites perturbées du problème à 2 corps
Auteur: S. Renner
Date de création: 04 avril 2011
L'objectif de cet exercice est de déterminer quels types de forces perturbatrices peuvent modifier le demi grand-axe ou l'excentricité d'une orbite.
Il est nécessaire de s'intéresser au préalable à la résolution du problème à 2 corps.
Ex: Orbites perturbées du problème à 2 corps
Loi de Planck en fréquence
Auteur: Stéphane Erard
Date de création: 07 mars 2013
La loi de Planck donnant le spectre du corps noir est souvent donnée en fonction de la longueur d'onde. L'objectif de cet exercice est de dériver cette loi en fonction de la fréquence du rayonnement. Cette expression est plus naturellement utilisée dans certains domaines, en particulier aux basses énergies (domaine radio) et aux basses températures (dans le milieu interstellaire par exemple).
Ex: loi de Planck en fréquence
Auteur: Stéphane Erard
 Loi de Planck en fréquence
Loi de Planck en fréquence
Difficulté : ☆
Temps : 30 min
On connaît la luminance du corps noir en fonction de la longueur d'onde, donnée par la loi de Planck (voir par exemple l'exercice sur la loi de Wien) :
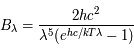
où 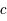 est la vitesse de la lumière dans le vide,
est la vitesse de la lumière dans le vide, 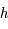 la constante de Planck,
la constante de Planck, 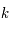 la constante de Boltzmann,
la constante de Boltzmann, 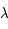 la longueur d'onde et
la longueur d'onde et 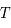 la température du corps noir.
la température du corps noir.
Cette expression est une luminance directionnelle, donnée habituellement en 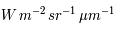 .
.
Question 1)
Donner l'expression de cette luminance en fonction de la fréquence du rayonnement.
Longueur d'onde et fréquence d'un rayonnement sont reliés par 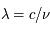
où c est la vitesse de la lumière dans le vide.
Question 2)
Comparer les graphiques de ces deux expressions en échelle linéaire.
Théorème des accroissements finis
Auteurs: Alain Vienne, Marc Fouchard
Les racines du polynôme de la méthode de Laplace
Auteur: Alain Vienne
Lors de la découverte d'un nouvel objet dans le système solaire, on souhaite rapidement connaitre sa trajectoire. Celle-ci est généralement héliocentrique et, dans un premier temps, on la suppose képlérienne. Or les observations terrestres donnent uniquement la direction de l'astre mais pas sa distance. La méthode de Laplace propose un moyen qui, à partir de 3 observations de direction faites à des dates assez rapprochées, donne les vecteurs position et la vitesse de l'astre. Le détail de la méthode peut être trouvé dans le cours suivant: Dynamique du système solaire. On peut y voir notamment que la méthode conduit à chercher les racines d'un polynôme de degré 8. Il y est affirmé qu'il y a 4 racines réelles (1 négative, 3 positives) et 4 complexes non réelles. C'est cette affirmation qui est étudiée dans l'exercice qui suit.
Le polynôme est de la forme:
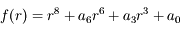
On sait que 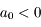 et qu'il existe au moins 2 solutions distinctes strictement positives. L'une des deux est
et qu'il existe au moins 2 solutions distinctes strictement positives. L'une des deux est  où
où 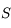 est la distance Terre-Soleil. On peut aller voir l'exercice qui vérifie cette racine ici. La deuxième solution distincte de
est la distance Terre-Soleil. On peut aller voir l'exercice qui vérifie cette racine ici. La deuxième solution distincte de 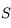 et strictement positive suppose que les 3 observations ont été bien faites et correspondent physiquement à un même objet du système solaire. Elle n'est pas garantie mathématiquement mais s'appuie sur l'argument que cette solution "doit exister".
et strictement positive suppose que les 3 observations ont été bien faites et correspondent physiquement à un même objet du système solaire. Elle n'est pas garantie mathématiquement mais s'appuie sur l'argument que cette solution "doit exister".
Voici à titre d'exemple le graphe du polynôme dans le cas de 3 observations de Jupiter à son opposition (courbe "complète" et un agrandissement):
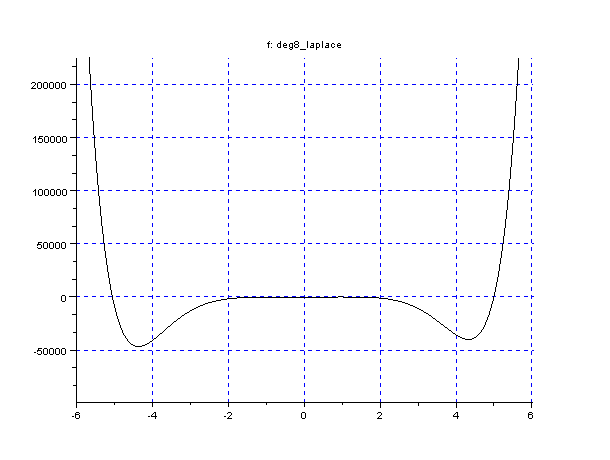
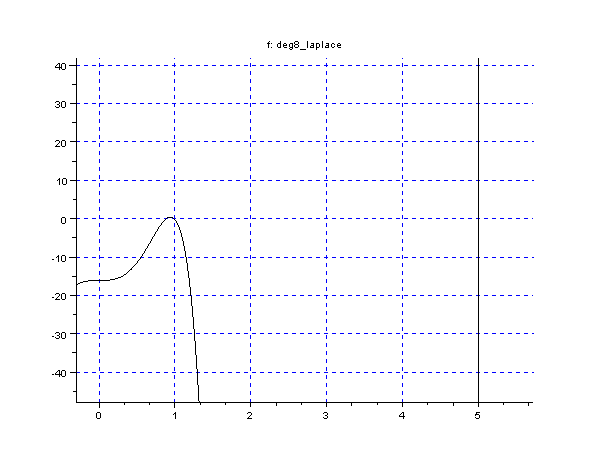
Le polynome de la méthode de Laplace dans le cas de 3 observations de Jupiter (courbe "complète" et un agrandissement). L'axe horizontal est gradué en ua. On note que ce polynôme n'est pas très bien conditionné car la vue d'ensemble ne donne pas une idée des racines ni même du nombre de ces racines. La deuxième figure est agrandissement sur la partie utile. On voit la racine
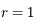
ua (
) et les 2 autres racines dont celle qui nous intéresse à 5 ua.
Ex: Les racines du polynôme de la méthode de Laplace
Auteur: Alain Vienne
 Les racines du polynôme de la méthode de Laplace
Les racines du polynôme de la méthode de Laplace
Difficulté : ☆☆
Temps : 1h
Soit un polynôme à coefficients réels de la forme:
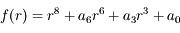
On sait que 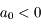 et qu'il existe au moins 2 solutions distinctes strictement positives.
et qu'il existe au moins 2 solutions distinctes strictement positives.
Question 1)
Calculer 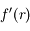 et étudier le polynôme
et étudier le polynôme 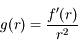 dans le cas où
dans le cas où 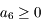
Question 2)
En déduire que 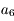 est strictement négatif
est strictement négatif
Voir que, dans ce cas, 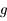 est strictement croissant puis utiliser le théorème des valeurs intermédiaires.
est strictement croissant puis utiliser le théorème des valeurs intermédiaires.
Question 3)
Montrer que 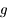 s'annule en un point
s'annule en un point 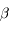 positif
positif
Utiliser le théorème de Rolle pour 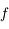 sur l'intervalle définie par ses 2 racines positives
sur l'intervalle définie par ses 2 racines positives
Question 5)
Monter que 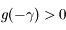 .
.
Question 7)
Etudier les 2 cas 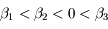 et
et 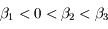 . Monter que le premier cas est impossible et que le deuxième cas conduit à une ou trois racines positives
. Monter que le premier cas est impossible et que le deuxième cas conduit à une ou trois racines positives
Dresser le tableau de variation de 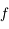 dans ces 2 cas.
dans ces 2 cas.
Les racines des polynômes de Legendre
Auteur: Alain Vienne
En Mécanique Céleste, on est souvent conduit à utiliser les polynômes de Legendre que l'on note ici 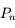 .
.
C'est le cas, par exemple, dans le développement du potentiel terrestre. Si on suppose que la Terre est un sphéroïde, le potentiel peut s'écrire:
![U(r,\varphi)=\frac{KM_T}{r} \ [1 - \sum_{m=1}^{\infty} J_{2m} (\frac{a_e}{r})^{2m} P_{2m}(\sin\varphi) \ ]](../pages_af/equations_af/equation51.png)
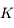 est la constante de gravitation de la Terre,
est la constante de gravitation de la Terre, 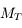 la masse totale de la Terre,
la masse totale de la Terre, 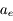 son rayon équatorial et
son rayon équatorial et 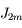 des coefficients numériques.
des coefficients numériques. 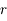 et
et 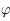 sont le rayon et la latitude du point pour lequel on évalue le potentiel
sont le rayon et la latitude du point pour lequel on évalue le potentiel 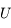 .
.
Un autre exemple d'utilisation est de considérer 2 corps 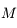 et
et 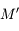 décrivant autour d'un centre
décrivant autour d'un centre 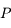 des orbites proches d'un mouvement elliptique. Pour décrire les perturbations (gravitationnelles) entre
des orbites proches d'un mouvement elliptique. Pour décrire les perturbations (gravitationnelles) entre 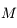 et
et 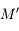 , on doit écrire l'inverse de la dsitance entre
, on doit écrire l'inverse de la dsitance entre 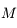 et
et 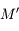 ,
, 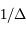 , en fonction de leurs éléments d'orbite. On montre facilement que:
, en fonction de leurs éléments d'orbite. On montre facilement que:
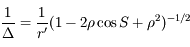
Avec 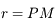 ,
, 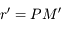 ,
, 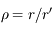 et
et 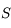 l'angle entre
l'angle entre 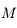 et
et 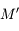 vu de
vu de 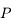 .
.
Cette dernière expression est développée en puissance de 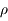 grâce aux polynômes de Legendre:
grâce aux polynômes de Legendre:
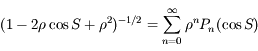
Ce développement est rapidement convergent si 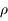 est petit. C'est le cas si, par exemple,
est petit. C'est le cas si, par exemple, 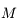 est la Terre,
est la Terre, 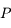 le Soleil et
le Soleil et 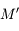 un satellite artificiel.
un satellite artificiel.
Plus de détails de ces développement peuvent être vus dans le cours de Mécanique Céleste de Luc Duriez.
Les polynômes de Legendre ont de nombreuses propriétés. Celle que nous allons utiliser dans l'exercice qui suit est la formule de Rodrigues:
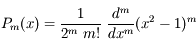
Cette formule va nous permettre de montrer que l'équation 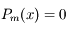 a toutes ses racines dans
a toutes ses racines dans ![[-1,+1]](../pages_af/equations_af/equation83.png) et en a
et en a 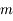 distinctes.
distinctes.
Ex: Les racines des polynômes de Legendre
Auteur: Alain Vienne
 Les racines des polynômes de Legendre
Les racines des polynômes de Legendre
Difficulté : ☆☆
Temps : 1h (pour une rédaction correcte)
Les polynômes de Legendre, bien connus en Mécanique Céleste, peuvent se déterminer par la formule de Rodrigues:
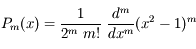
Projection de Mollweide
Auteur: Marc Fouchard
La projection de Mollweide est la projection d'une sphère sur un plan qui conserve les aires au sacrifice de la conservation des distances et des formes. La projection d'une sphère rempli une ellipse dont le petit axe est le double du grand axe.
L'avantage d'une telle projection en astronomie est qu'elle permet d'avoir une idée globale de la répartition d'une certaine quantité sur la sphère céleste par unité de surface (ou stéradian). Par exemple, l'image suivante montre la répartition du rayonnement du fond cosmologique sur une projection de Mollweide de la sphère céleste.
Comme ce rayonnement est mesuré par unité de surface (ou par stéradian), la conservation des aires est ici fondamentale pour bien visualiser les données.
Le rayonnement du fond cosmologique par WMAP
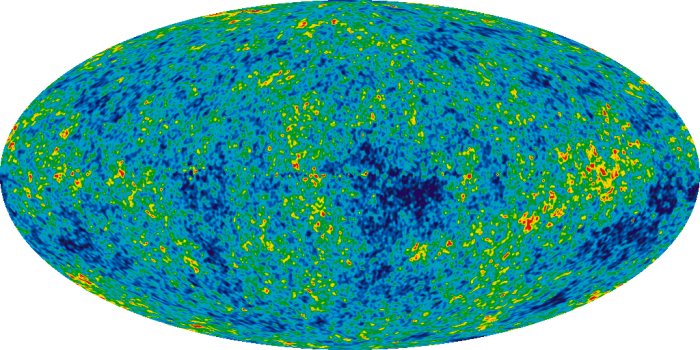
Répartition du rayonnement du fond cosmologique observé par le satellite WMAP (l'échelle de couleur est entre +/- 200 micro Kelvin par rapport à une valeur moyenne) sur une projection de Mollweide de la sphère céleste. Le plan de référence est celui de la Voie Lactée dont le rayonnement a été soustrait.
Crédit :
NASA/WMAP
Sur une sphère, on défini un système de coordonnées en choisissant un plan de référence (par exemple l'équateur), à partir duquel seront
mesurées les latitudes, notées 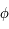 , un méridien de référence (par exemple le méridien de Greenwich) à partir duquel sont mesurées les longitudes, notées
, un méridien de référence (par exemple le méridien de Greenwich) à partir duquel sont mesurées les longitudes, notées 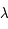 .
Pour chaque angle un sens positif est défini (par exemple vers le nord pour les latitudes et vers l'ouest pour les longitudes).
.
Pour chaque angle un sens positif est défini (par exemple vers le nord pour les latitudes et vers l'ouest pour les longitudes).
Les coordonnées 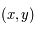 par la projection de Mollweide d'un point de coordonnées
par la projection de Mollweide d'un point de coordonnées 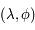 de la sphère céleste sont définies par:
de la sphère céleste sont définies par:
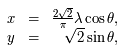
où la longitude 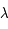 est mesurée entre
est mesurée entre 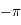 et
et 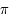 et
et 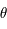 est un angle auxiliaire défini par :
est un angle auxiliaire défini par :
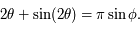 (*)
(*)
L'équation (*) ne peut être résolue analytiquement. Le but de cet exercice est de trouver une méthode permettant de déterminer 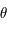 afin de pouvoir calculer
afin de pouvoir calculer 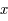 et
et 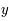 .
.
Ex : projection de Mollweide
Auteur: Marc Fouchard
 projection de Mollweide
projection de Mollweide
Difficulté : ☆☆
Temps : 1h30
Question 1)
Nous allons commencer par étudier la fonction:
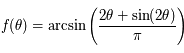 ,
,
sur l'intervalle ![I=[-\pi/2,\pi/2]](../pages_af/equations_af/equation124.png) .
.
Montrer que 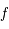 est définie et continue sur
est définie et continue sur 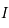 et qu'elle est impaire.
et qu'elle est impaire.
Question 2)
Montrer que 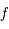 est dérivable sur
est dérivable sur ![]-\pi/2, \pi/2[](../pages_af/equations_af/equation137.png) , puis en prolongeant par continuité sur
, puis en prolongeant par continuité sur 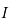 .
.
Question 8)
Montrer que la suite définie par 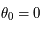 et
et 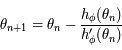 converge vers
converge vers 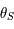 .
.
Extrema
Auteurs: Marc Fouchard, Jérôme Thiébaut
Loi de Wien
Ex : loi de Wien
Auteur: Marc Fouchard
 Loi de Wien
Loi de Wien
Difficulté : ☆☆
Temps : 2h
Question 3)
En déduire qu'il doit exister un maximum pour 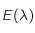 sur
sur 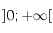 .
.
Etoile à neutron
Auteur : Jérôme Thiébaut
Une étoile à neutron constitue l'étape ultime d'évolution des étoiles de masses inférieures à trois masses solaires. Ayant brulé tout son carburant, l'étoile devient une supernova, elle éjecte ses couches extérieures et son coeur s'éffondre sur lui même. Les électrons et les protons fusionnent ensemble et se transforment en neutrons. La densité devient alors comparable à celle de la matière nucléaire et la température est de l'ordre de 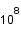 K.
Le but de cet exercice est de déterminer grâce à un modèle simple le rayon d'équilibre de ces étoiles.
K.
Le but de cet exercice est de déterminer grâce à un modèle simple le rayon d'équilibre de ces étoiles.
Ex: Etoile à neutron
Auteur: Jérôme Thiébaut
 Etoile à neutron
Etoile à neutron
Difficulté : ☆
Temps : 45 min
On assimile l'étoile à neutron à un gaz parfait de neutrons contenu dans une sphère. La densité d'états (ou fonction de distribution) de l'impulsion 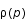 est la suivante:
est la suivante: 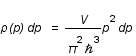 , où V est le volume et
, où V est le volume et 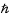 la constante de Planck réduite.
la constante de Planck réduite.
Question 1)
On définit la densité de particule n:
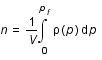 où
où 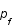 est l'impulsion de Fermi, c'est à dire l'impulsion maximale.
Exprimer n en fonction de
est l'impulsion de Fermi, c'est à dire l'impulsion maximale.
Exprimer n en fonction de 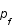 .
.
Question 2)
Exprimer l'impulsion de Fermi en fonction de la masse du neutron, m, celle de l'étoile, M, et du rayon de l'étoile, R.
Calculer d'abord la densité de particules en fonction des caractéristiques de l'étoile.
Question 4)
L'énergie du gaz E vallant 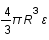 , l'exprimer en fonction de l'impulsion de Fermi puis en fonction des caractéristiques de l'étoile et de la masse du neutron.
, l'exprimer en fonction de l'impulsion de Fermi puis en fonction des caractéristiques de l'étoile et de la masse du neutron.
Question 5)
L'énergie gravitationnelle de l'étoile est 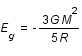 , où G est la constante de gravitation. L'équilibre est atteint lorsque l'énergie totale (celle du gaz plus celle gravitationnelle) de l'étoile est minimum. Calculer le rayon
, où G est la constante de gravitation. L'équilibre est atteint lorsque l'énergie totale (celle du gaz plus celle gravitationnelle) de l'étoile est minimum. Calculer le rayon 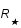 qui minimise l'énergie en fonction de la masse de l'étoile et des constantes m, G et
qui minimise l'énergie en fonction de la masse de l'étoile et des constantes m, G et 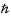 . Calculer ce rayon pour le soleil.
. Calculer ce rayon pour le soleil.
Trouver le rayon qui minimise l'énergie revient à résoudre 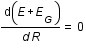 .
.
Sphère photonique
Auteur: Jérôme Thiébaut
En relativité générale la gravitation n'est pas une force mais une déformation de l'espace temps due aux corps qu'il contient. Par conséquent, la métrique, c'est à dire la manière de mesurer les distances, s'en trouve transformée par rapport aux distances euclidiennes usuelles. La métrique de Schwarzschild est une métrique applicable à un corps massif central statique ou en rotation lente. Cette métrique s'applique à l'extérieur du corps en question et n'est plus valable en son sein. Elle permet de plus, à grande distance ou dans le cas de potentiel faible, de retrouver la gravitation newtonnienne.
Le but de cet exercice est de montrer que pour des trous noirs, il existe une orbite circulaire en deça de laquelle il est impossible d'orbiter, et que cette orbite correspond à la trajectoire de photons.
Ex: Sphère photonique
Réponses aux exercices
pages_def/exo-retrogradation-mars.html
Exercice
'Rétrogradation de Mars'
-
Question 1
Solution :
Pour la Terre on a :
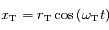
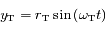 .
.
Et pour Mars on a :
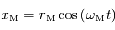
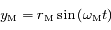 .
.
On en déduit :
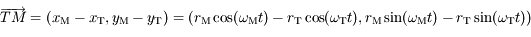 .
.
On en déduit:
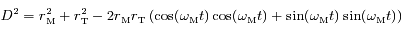
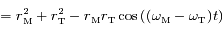 ,
,
et
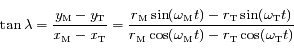 . Cette fonction n'est pas définie lorsque
. Cette fonction n'est pas définie lorsque 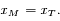
-
Question 2
Solution :
On a:
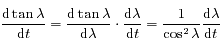 .
.
Or
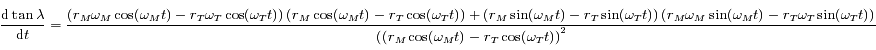
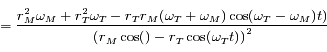 .
.
Le signe de 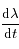 est celui du numérateur de l'expression ci-dessus.
Ainsi, quand
est celui du numérateur de l'expression ci-dessus.
Ainsi, quand 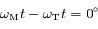 , le signe de la dérivée est celui de
, le signe de la dérivée est celui de 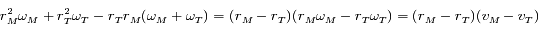 ,
oùt
,
oùt 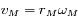 et
et 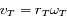 .
.
Or d'après la propriété dérivant de la troisième loi de Kepler, on a
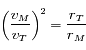 . Ainsi, pour Mars on a
. Ainsi, pour Mars on a 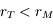 et
et 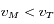 , donc la dérivée est négative.
De même on montre que pour
, donc la dérivée est négative.
De même on montre que pour 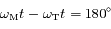 , la dérivée est positive.
, la dérivée est positive.
On en conclue qu'effectivement lors de l'opposition ( 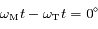 ), le mouvement de Mars est rétrograde, alors qu'à la conjonction
), le mouvement de Mars est rétrograde, alors qu'à la conjonction 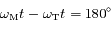 , le mouvement est prograde.
, le mouvement est prograde.
-
Question 3
Solution :
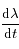 s'annulle lorsque
s'annulle lorsque 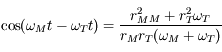 , soit
, soit 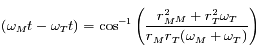 .
.
Ce qui nous donne, à 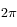 près, deux solutions opposées l'une de l'autre.
près, deux solutions opposées l'une de l'autre.
-
Question 4
Solution :
On a 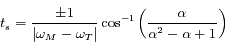 , d'où la durée de la rétrogradation
, d'où la durée de la rétrogradation 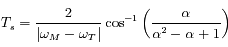 .
.
Pour Mars, cette durée est égale à 72,8 jours.
pages_def/exo-perturb-orbit.html
Exercice
'Orbites perturbées du problème à 2 corps'
pages_def/exo-planck-fq.html
Exercice
'Loi de Planck en fréquence'
-
Question 1
Aide :
Longueur d'onde et fréquence d'un rayonnement sont reliés par 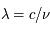
où c est la vitesse de la lumière dans le vide.
Solution :
Les intégrales en 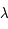 et
et 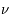 sont égales, elles donnent toutes deux la luminance intégrale du corps noir (loi de Stefan) :
sont égales, elles donnent toutes deux la luminance intégrale du corps noir (loi de Stefan) :
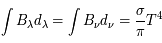
En dérivant, on obtient :
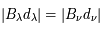 où
où 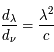
Le changement de variable donne directement :
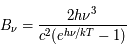 (donné couramment en
(donné couramment en  )
)
-
Question 2
Solution :
Corps noir en longueur d'onde
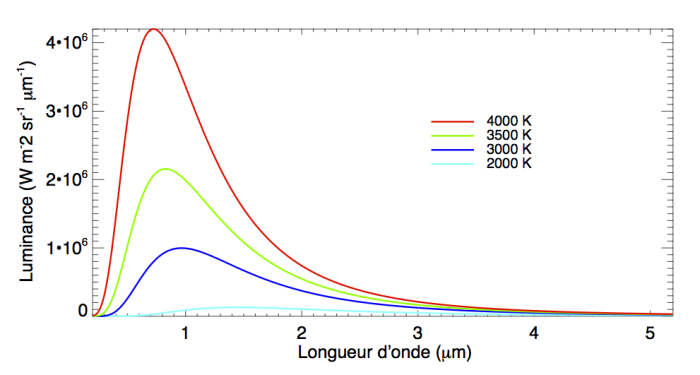
Corps noir en fréquence
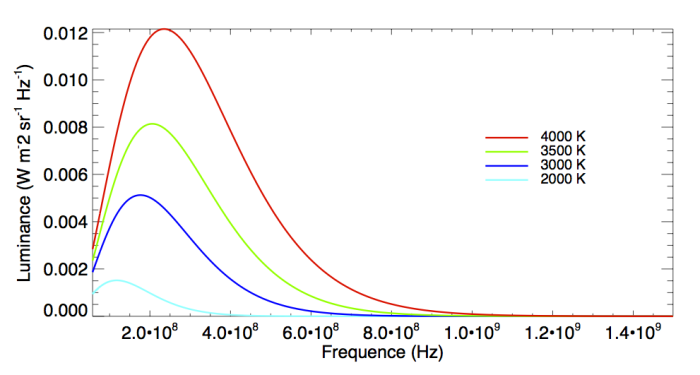
Outre la forme différente, on voit que le maximum se déplace en direction inverse quand la température augmente.
pages_af/exo-racines-laplace.html
Exercice
'Les racines du polynôme de la méthode de Laplace'
pages_af/exo-poly-legendre-racines.html
Exercice
'Les racines des polynômes de Legendre'
pages_af/exo-proj-mollweide-af.html
Exercice
'projection de Mollweide'
-
Question 1
Solution :
La fonction 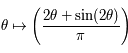 est continue dérivable et strictement croissante. Ainsi l'image de
est continue dérivable et strictement croissante. Ainsi l'image de  est l'ensemble
est l'ensemble ![[-1, 1]](../pages_af/equations_af/equation129.png) .
Donc la fonction
.
Donc la fonction  est bien définie sur
est bien définie sur 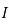 .
.
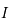 est symétrique par rapport à zéro,
est symétrique par rapport à zéro, 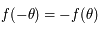 . Donc
. Donc 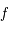 est une fonction impaire sur
est une fonction impaire sur 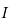 .
.
-
Question 2
Aide :
Pour le prolongement par continuité en 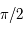 de la dérivée de
de la dérivée de 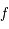 , on pourra faire le changement de variable
, on pourra faire le changement de variable 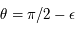 et faire le développement limité en zéro.
et faire le développement limité en zéro.
Solution :
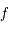 est dérivable sur
est dérivable sur ![]-\pi/2, \pi/2[](../pages_af/equations_af/equation143.png) par composition de fonction continues et dérivables.
On a:
par composition de fonction continues et dérivables.
On a:
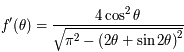 .
.
Cette fonction n'est pas définie pour 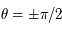 . On pose alors
. On pose alors 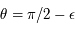 . Ainsi:
. Ainsi:
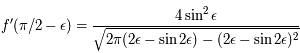 .
.
Les développements limités en zéro nous indiquent que le dénominateur est de l'ordre de 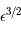 alors que le numérateur est de l'ordre de
alors que le numérateur est de l'ordre de 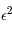 . Ainsi on a:
. Ainsi on a: 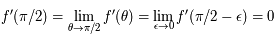 . Comme
. Comme 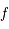 est impaire on a de même en prolongeant par continuité
est impaire on a de même en prolongeant par continuité 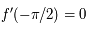 .
.
-
Question 3
Solution :
D'après la question précédente, on voit que 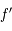 est strictement supérieur à zéro sur
est strictement supérieur à zéro sur ![]-\pi/2, \pi/2[](../pages_af/equations_af/equation159.png) , et ne s'annule qu'en
, et ne s'annule qu'en 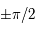 .
Ainsi
.
Ainsi 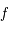 est strictement croissante sur
est strictement croissante sur 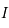 . Comme
. Comme 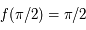 , par parité on en déduit que
, par parité on en déduit que 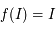 .
Donc
.
Donc 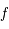 est une fonction bijective de
est une fonction bijective de 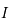 dans lui-même. Il existe donc une fonction réciproque
dans lui-même. Il existe donc une fonction réciproque 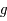 .
D'après les propriétés de
.
D'après les propriétés de 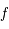 , on en déduit que
, on en déduit que 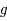 est une fonction impaire définie et continue sur
est une fonction impaire définie et continue sur 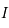 et dérivable sur
et dérivable sur 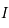 ouvert.
De plus comme on a
ouvert.
De plus comme on a ![f([0,\pi/2])=[0,\pi/2]](../pages_af/equations_af/equation172.png) , on a aussi
, on a aussi ![g([0,\pi/2])=[0,\pi/2]](../pages_af/equations_af/equation173.png) .
.
-
Question 4
Solution :
- Si
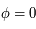 , alors l'équation (*) admet
, alors l'équation (*) admet 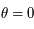 comme solution (en effet
comme solution (en effet 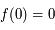 , c'est-à-dire
, c'est-à-dire 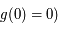 . Ainsi
. Ainsi  et
et 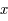 varie de
varie de 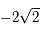 à
à 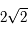 lorsque
lorsque 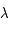 varie de
varie de 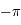 à
à 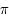 .
.
- Pour le pôle nord, on a
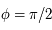 . Or
. Or 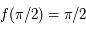 , soit
, soit 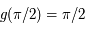 , ainsi
, ainsi 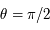 . L'image du pôle nord est
. L'image du pôle nord est 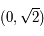 .
Par symétrie, le pôle Sud a pour image
.
Par symétrie, le pôle Sud a pour image 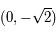 .
.
- Dans ce cas on a
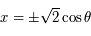 et
et 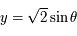 (le signe "+" correspond à la longitude positive). Les points se trouvent donc sur un demi-cercle centré à l'origine et de rayon
(le signe "+" correspond à la longitude positive). Les points se trouvent donc sur un demi-cercle centré à l'origine et de rayon 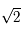 se trouvant à droite de l'axe des ordonnées pour la longitude positive et à gauche pour la longitude négative. Comme un méridien correspond à l'ensemble des latitudes
se trouvant à droite de l'axe des ordonnées pour la longitude positive et à gauche pour la longitude négative. Comme un méridien correspond à l'ensemble des latitudes ![\phi \in [-\pi/2,\pi/2]](../pages_af/equations_af/equation199.png) , chaque demi-cercle est décrit complètement d'après la propriété de la fonction
, chaque demi-cercle est décrit complètement d'après la propriété de la fonction 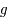 :
: ![g([-\pi/2,\pi/2])=[-\pi/2,\pi/2]](../pages_af/equations_af/equation201.png) .
.
- Dans ce cas on a
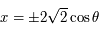 et
et 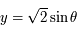 . Comme à la question précédente sauf que les points se trouvent sur deux demi-ellipses d'une ellipse centrée à l'origine et de demi-petit axe
. Comme à la question précédente sauf que les points se trouvent sur deux demi-ellipses d'une ellipse centrée à l'origine et de demi-petit axe 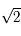 parallèle à l'axe des ordonnées et de demi-grand axe
parallèle à l'axe des ordonnées et de demi-grand axe 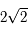 . Toute l'ellipse est décrite, pour la même raison que précédemment.
. Toute l'ellipse est décrite, pour la même raison que précédemment.
- Si on note
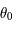 la solution de l'équation (*) pour la latitude
la solution de l'équation (*) pour la latitude 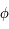 , i.e.
, i.e. 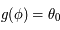 , alors
, alors 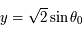 et
et 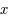 varie de
varie de 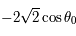 à
à 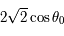 lorsque
lorsque 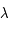 varie de
varie de 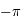 à
à 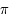 . C'est une corde de l'ellipse parallèle à l'axe des abcisses.
. C'est une corde de l'ellipse parallèle à l'axe des abcisses.
-
Question 5
Solution :
On a 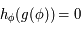 , or
, or 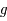 est impaire, donc
est impaire, donc 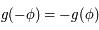 , ce qui répond au premier point. Ensuite, comme
, ce qui répond au premier point. Ensuite, comme ![g([0,\pi/2])=[0,\pi/2]](../pages_af/equations_af/equation232.png) on en déduit que si
on en déduit que si ![\phi\in[0,\pi/2]](../pages_af/equations_af/equation233.png) alors la solution de
alors la solution de 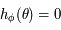 est dans
est dans ![[0,\pi/2]](../pages_af/equations_af/equation235.png) . Les deux dernières égalités viennent directement du fait que
. Les deux dernières égalités viennent directement du fait que 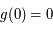 et
et 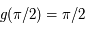 .
.
-
Question 6
Solution :
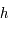 est définie continue dérivable sur
est définie continue dérivable sur 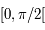 comme composée de fonctions définies continues et dérivables. On a
comme composée de fonctions définies continues et dérivables. On a 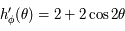 qui est continue et strictement positive sur
qui est continue et strictement positive sur 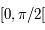 . Elle est aussi dérivable, avec
. Elle est aussi dérivable, avec 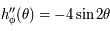 .
. 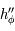 est strictement négative sur
est strictement négative sur ![]0,\pi/2[](../pages_af/equations_af/equation251.png) et nulle en 0. Ainsi
et nulle en 0. Ainsi 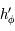 est strictement décroissante sur
est strictement décroissante sur 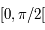 .
.
-
Question 7
Aide :
On utilisera le théorème des accroissements finis.
Solution :
L'équation de la tangente est 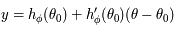 . Pour
. Pour 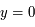 on obtient
on obtient 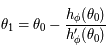 .
Comme
.
Comme 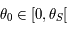 , que
, que 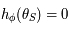 et que
et que 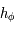 est croissante, on en déduit que
est croissante, on en déduit que 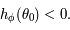 De plus
De plus 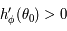 ainsi
on a bien
ainsi
on a bien 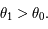 D'après le théorème des accroissements finis, il existe
D'après le théorème des accroissements finis, il existe ![\theta\in]\theta_0,\theta_S[](../pages_af/equations_af/equation275.png) tel que
tel que 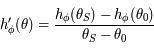 . Ainsi, en considérant
. Ainsi, en considérant 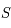 comme le point d'intersection entre l'axe des abscisses et la droite passant par
comme le point d'intersection entre l'axe des abscisses et la droite passant par 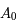 et de coefficient directeur
et de coefficient directeur 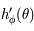 , on a
, on a 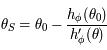 . Comme
. Comme 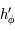 est une fonction strictement décroissante sur
est une fonction strictement décroissante sur ![]\theta_0, \theta_S[](../pages_af/equations_af/equation282.png) , on en déduit que
, on en déduit que 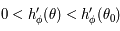 , soit
, soit 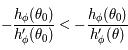 .
Ainsi on a bien
.
Ainsi on a bien 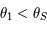 .
.
-
Question 8
Solution :
On sait que si ![\phi\in]0,\pi/2[](../pages_af/equations_af/equation300.png) alors
alors ![\theta_S\in]0,\pi/2[](../pages_af/equations_af/equation301.png) . Autrement dit
. Autrement dit 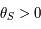 , donc
, donc 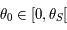 . Ainsi d'après la question précédente on sait que
. Ainsi d'après la question précédente on sait que 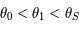 . Donc
. Donc 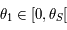 .
Si on suppose maintenant
.
Si on suppose maintenant 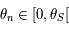 alors, toujours d'après la question précédente on a
alors, toujours d'après la question précédente on a 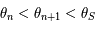 , en outre
, en outre 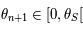 .
Ainsi,
.
Ainsi, 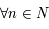 on a
on a 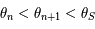 . Donc la suite
. Donc la suite 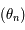 est croissante et majorée, donc elle converge vers une limite
est croissante et majorée, donc elle converge vers une limite 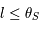 .
Par continuité de
.
Par continuité de 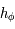 et
et 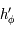 , on a
, on a 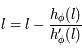 , et comme
, et comme 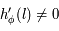 , on en déduit que
, on en déduit que 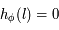 , donc
, donc 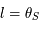 .
.
pages_extremas/exo-loi-de-wien-extremas.html
Exercice
'Loi de Wien'
pages_extremas/ex-neutron-star.html
Exercice
'Etoile à neutron'
-
Question 1
Solution :
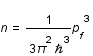
-
Question 2
Aide :
Calculer d'abord la densité de particules en fonction des caractéristiques de l'étoile.
Solution :
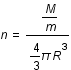
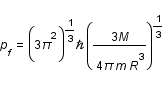
-
Question 3
Solution :
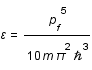
-
Question 4
Solution :
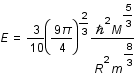
-
Question 5
Aide :
Trouver le rayon qui minimise l'énergie revient à résoudre 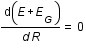 .
.
Solution :
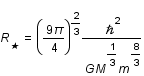 L'application numérique donne pour une étoile d'une masse solaire un rayon de 12km !
L'application numérique donne pour une étoile d'une masse solaire un rayon de 12km !
pages_extremas/ex-sph-phot.html
Exercice
'Sphère photonique'

 et Mars
et Mars  se déplacent
se déplacent 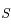 . Soit
. Soit 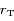 et
et 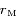 les rayons respectives des
les rayons respectives des 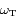 ,
, 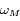 leur
leur 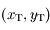 et
et 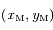 les coordonnées respectives de la Terre et de Mars. On suppose qu'initialement le Soleil, la Terre et Mars sont alignés dans cet ordre sur l'axe des abscisses du côté des abscisses positives.
les coordonnées respectives de la Terre et de Mars. On suppose qu'initialement le Soleil, la Terre et Mars sont alignés dans cet ordre sur l'axe des abscisses du côté des abscisses positives.
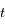 . Soit
. Soit 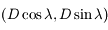 les coordonnées du vecteur
les coordonnées du vecteur 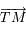 . En déduire une expression de
. En déduire une expression de 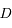 et de
et de 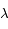 en fonction de
en fonction de 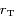 ,
, 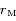 ,
, 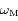 ,
, 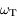 et
et 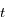 .
.
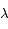 par rapport au temps, puis déterminer son signe pour
par rapport au temps, puis déterminer son signe pour 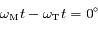 et
et 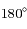 .
On utilisera la propriété
.
On utilisera la propriété 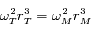 qui dérive de la troisième loi de Kepler.
Conclure.
qui dérive de la troisième loi de Kepler.
Conclure.
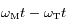 lorsque
lorsque 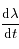 s'annule. Ces positions correspondent aux stations de Mars. On notera dans la suite
s'annule. Ces positions correspondent aux stations de Mars. On notera dans la suite 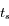 un instant conrrespondant à une station.
un instant conrrespondant à une station.
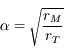 . En déduire la durée de la rétrogradation.
. En déduire la durée de la rétrogradation.
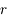 ) est soumis à une force perturbatrice de la forme
) est soumis à une force perturbatrice de la forme 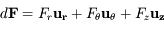 , où
, où 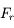 ,
, 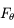 ,
, 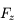 sont respectivement les composantes (constantes) radiale, tangentielle et normale de la force, et
sont respectivement les composantes (constantes) radiale, tangentielle et normale de la force, et 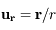 ,
, 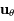 ,
, 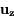 des vecteurs orthonormés unitaires. Cette force est suffisamment faible pour que la trajectoire de l'objet reste keplerienne.
des vecteurs orthonormés unitaires. Cette force est suffisamment faible pour que la trajectoire de l'objet reste keplerienne.
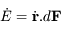 due à la force
due à la force 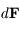 . Sachant de plus que
. Sachant de plus que 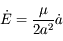 avec
avec 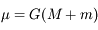 , montrer quels types de forces vont modifier le
, montrer quels types de forces vont modifier le 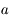 en calculant
en calculant 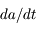 .
.
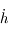 due à
due à 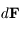 , montrer quels types de forces modifient l'
, montrer quels types de forces modifient l'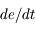 .
.
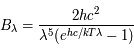
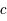 est la vitesse de la lumière dans le vide,
est la vitesse de la lumière dans le vide, 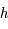 la constante de Planck,
la constante de Planck, 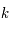 la constante de Boltzmann,
la constante de Boltzmann, 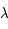 la longueur d'onde et
la longueur d'onde et 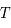 la température du corps noir.
la température du corps noir.
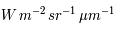 .
.
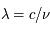
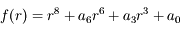
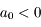 et qu'il existe au moins 2 solutions distinctes strictement positives. L'une des deux est
et qu'il existe au moins 2 solutions distinctes strictement positives. L'une des deux est 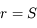 où
où 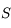 est la distance Terre-Soleil. On peut aller voir l'exercice qui vérifie cette racine
est la distance Terre-Soleil. On peut aller voir l'exercice qui vérifie cette racine 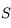 et strictement positive suppose que les 3 observations ont été bien faites et correspondent physiquement à un même objet du système solaire. Elle n'est pas garantie mathématiquement mais s'appuie sur l'argument que cette solution "doit exister".
et strictement positive suppose que les 3 observations ont été bien faites et correspondent physiquement à un même objet du système solaire. Elle n'est pas garantie mathématiquement mais s'appuie sur l'argument que cette solution "doit exister".


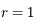 ua (
ua (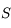 ) et les 2 autres racines dont celle qui nous intéresse à 5 ua.
) et les 2 autres racines dont celle qui nous intéresse à 5 ua.
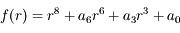
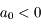 et qu'il existe au moins 2 solutions distinctes strictement positives.
et qu'il existe au moins 2 solutions distinctes strictement positives.
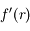 et étudier le polynôme
et étudier le polynôme 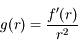 dans le cas où
dans le cas où 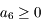
 est strictement négatif
est strictement négatif
 est strictement croissant puis utiliser le théorème des valeurs intermédiaires.
est strictement croissant puis utiliser le théorème des valeurs intermédiaires.
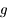 s'annule en un point
s'annule en un point 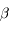 positif
positif
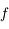 sur l'intervalle définie par ses 2 racines positives
sur l'intervalle définie par ses 2 racines positives
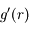 peut donc s'écrire
peut donc s'écrire 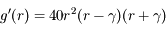 (avec
(avec 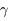 positif). Monter que
positif). Monter que 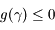 .
.
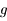 et voir qu'on ne pourrait alors avoir l'existence de
et voir qu'on ne pourrait alors avoir l'existence de 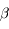 .
.
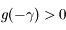 .
.
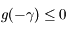 et dresser le tableau de variation de
et dresser le tableau de variation de 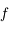 . On n'oublie pas que
. On n'oublie pas que 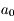 est négatif.
est négatif.
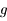 s'annule en
s'annule en 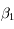 ,
, 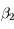 et
et 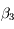 tels que
tels que 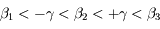
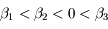 et
et 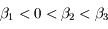 . Monter que le premier cas est impossible et que le deuxième cas conduit à une ou trois racines positives
. Monter que le premier cas est impossible et que le deuxième cas conduit à une ou trois racines positives
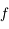 dans ces 2 cas.
dans ces 2 cas.
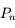 .
.
![U(r,\varphi)=\frac{KM_T}{r} \ [1 - \sum_{m=1}^{\infty} J_{2m} (\frac{a_e}{r})^{2m} P_{2m}(\sin\varphi) \ ]](../pages_af/equations_af/equation51.png)
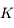 est la constante de gravitation de la Terre,
est la constante de gravitation de la Terre, 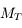 la masse totale de la Terre,
la masse totale de la Terre, 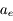 son rayon équatorial et
son rayon équatorial et 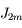 des coefficients numériques.
des coefficients numériques. 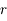 et
et 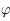 sont le rayon et la latitude du point pour lequel on évalue le potentiel
sont le rayon et la latitude du point pour lequel on évalue le potentiel 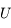 .
.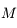 et
et 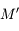 décrivant autour d'un centre
décrivant autour d'un centre 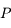 des orbites proches d'un mouvement elliptique. Pour décrire les perturbations (gravitationnelles) entre
des orbites proches d'un mouvement elliptique. Pour décrire les perturbations (gravitationnelles) entre 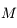 et
et 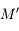 , on doit écrire l'inverse de la dsitance entre
, on doit écrire l'inverse de la dsitance entre 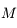 et
et 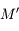 ,
, 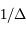 , en fonction de leurs éléments d'orbite. On montre facilement que:
, en fonction de leurs éléments d'orbite. On montre facilement que:
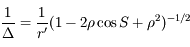
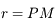 ,
, 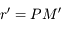 ,
, 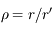 et
et 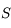 l'angle entre
l'angle entre 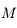 et
et 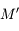 vu de
vu de 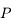 .
.
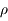 grâce aux polynômes de Legendre:
grâce aux polynômes de Legendre:
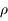 est petit. C'est le cas si, par exemple,
est petit. C'est le cas si, par exemple, 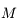 est la Terre,
est la Terre, 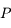 le Soleil et
le Soleil et 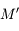 un satellite artificiel.
un satellite artificiel.
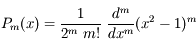
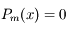 a toutes ses racines dans
a toutes ses racines dans ![[-1,+1]](../pages_af/equations_af/equation83.png) et en a
et en a 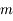 distinctes.
distinctes.
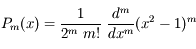
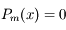 a toutes ses racines dans
a toutes ses racines dans ![[-1,+1]](../pages_af/equations_af/equation87.png) et en a
et en a 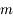 distinctes.
distinctes.
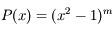 a
a 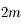 racines. Elles sont non disctinctes car il s'agit de
racines. Elles sont non disctinctes car il s'agit de 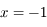 et
et 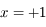 chacune d'elles étant d'ordre
chacune d'elles étant d'ordre 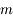 .
.
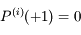 et
et 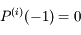 pour tout
pour tout 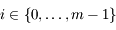 , où
, où
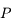 sur l'intervalle
sur l'intervalle ![[-1,+1]](../pages_af/equations_af/equation98.png)
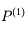 qui s'annulle en
qui s'annulle en 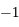 ,
, 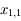 et
et 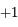 (ces trois racines sont distinctes)
(ces trois racines sont distinctes)
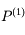 sur l'intervalle
sur l'intervalle ![[-1,x_{1,1}]](../pages_af/equations_af/equation104.png) , puis sur
, puis sur ![[x_{1,1},+1]](../pages_af/equations_af/equation105.png) . On a donc les racines
. On a donc les racines 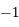 ,
, 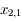 ,
, 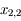 et
et 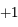 (ces quatres racines sont distinctes). Rédigez ensuite la récurrence. Une rédaction propre n'est pas si aisée. Faites la avec soin et choissisez bien vos notations (par exemple, bien différencier l'indice du polynôme et l'indice de la récurrence).
(ces quatres racines sont distinctes). Rédigez ensuite la récurrence. Une rédaction propre n'est pas si aisée. Faites la avec soin et choissisez bien vos notations (par exemple, bien différencier l'indice du polynôme et l'indice de la récurrence).

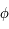 , un méridien de référence (par exemple le méridien de Greenwich) à partir duquel sont mesurées les longitudes, notées
, un méridien de référence (par exemple le méridien de Greenwich) à partir duquel sont mesurées les longitudes, notées 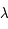 .
Pour chaque angle un sens positif est défini (par exemple vers le nord pour les latitudes et vers l'ouest pour les longitudes).
.
Pour chaque angle un sens positif est défini (par exemple vers le nord pour les latitudes et vers l'ouest pour les longitudes).
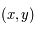 par la projection de Mollweide d'un point de coordonnées
par la projection de Mollweide d'un point de coordonnées 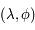 de la sphère céleste sont définies par:
de la sphère céleste sont définies par:
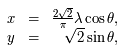
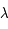 est mesurée entre
est mesurée entre 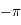 et
et 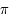 et
et 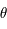 est un angle auxiliaire défini par :
est un angle auxiliaire défini par :
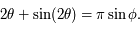 (*)
(*)
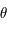 afin de pouvoir calculer
afin de pouvoir calculer 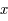 et
et 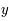 .
.
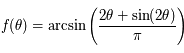 ,
,
![I=[-\pi/2,\pi/2]](../pages_af/equations_af/equation124.png) .
.
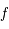 est définie et continue sur
est définie et continue sur  et qu'elle est impaire.
et qu'elle est impaire.
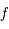 est dérivable sur
est dérivable sur ![]-\pi/2, \pi/2[](../pages_af/equations_af/equation137.png) , puis en prolongeant par continuité sur
, puis en prolongeant par continuité sur 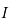 .
.
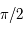 de la dérivée de
de la dérivée de 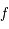 , on pourra faire le changement de variable
, on pourra faire le changement de variable 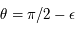 et faire le développement limité en zéro.
et faire le développement limité en zéro.
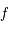 est strictement croissante de
est strictement croissante de 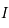 dans lui-même et donc qu'il existe une fonction réciproque, notée
dans lui-même et donc qu'il existe une fonction réciproque, notée 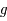 .
Déterminer les propriétés principales de
.
Déterminer les propriétés principales de 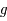 et en particulier que
et en particulier que ![g([0,\pi/2])=[0,\pi/2]](../pages_af/equations_af/equation157.png)
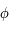 donné,
donné, 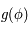 est la solution de l'équation (*).
est la solution de l'équation (*).
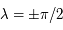 .
.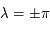 .
.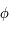 .
.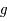 n'est pas définie analytiquement. On va montrer ici qu'on peut estimer
n'est pas définie analytiquement. On va montrer ici qu'on peut estimer 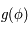 par la méthode de Newton-Raphson.
Soit
par la méthode de Newton-Raphson.
Soit 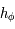 la fonction définie sur
la fonction définie sur ![[-\pi/2,\pi/2]](../pages_af/equations_af/equation219.png) par :
par :
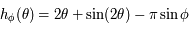 .
.
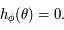
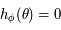 alors
alors 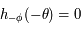 et que si
et que si ![\phi\in[0,\pi/2]](../pages_af/equations_af/equation224.png) alors la solution de
alors la solution de 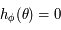 est dans
est dans ![[0,\pi/2]](../pages_af/equations_af/equation226.png) .
De même montrer que
.
De même montrer que 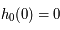 et
et 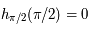 .
.
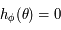 pour
pour ![\phi\in]0,\pi/2[](../pages_af/equations_af/equation239.png) . On sait déjà que la solution se trouve dans
. On sait déjà que la solution se trouve dans ![]0,\pi/2[](../pages_af/equations_af/equation240.png) d'après la question 3.
Montrer que, pour
d'après la question 3.
Montrer que, pour ![\phi\in]0,\pi/2[](../pages_af/equations_af/equation241.png) ,
, 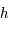 est définie continue dérivable et strictement croissante sur
est définie continue dérivable et strictement croissante sur 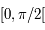 et que sa dérivée est définie continue, strictement positive et strictement décroissante sur
et que sa dérivée est définie continue, strictement positive et strictement décroissante sur 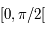 .
.
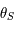 la solution de
la solution de 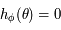 . Soit
. Soit 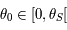 . On note
. On note 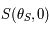 et
et 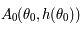 les points de la courbe représentative
les points de la courbe représentative 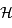 de
de 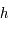 dans un repère orthonormé.
On note
dans un repère orthonormé.
On note 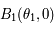 , le point d'intersection de la tangente en
, le point d'intersection de la tangente en 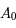 à
à 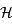 avec l'axe des abscisses.
Montrer que
avec l'axe des abscisses.
Montrer que 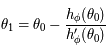 et que
et que 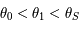 .
.
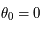 et
et 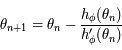 converge vers
converge vers 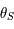 .
.
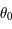 . La figure ci-dessous montre le nombre d'itérations nécessaires pour attendre un précision relative de l'ordre de
. La figure ci-dessous montre le nombre d'itérations nécessaires pour attendre un précision relative de l'ordre de 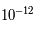 sur
sur 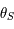 en fonction de
en fonction de 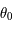 et
et 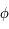 .
On voit que pour certains choix la convergence est très mauvaise voire impossible. Par contre avec
.
On voit que pour certains choix la convergence est très mauvaise voire impossible. Par contre avec 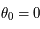 , la méthode converge pour toute valeur de
, la méthode converge pour toute valeur de 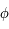 même si ce n'est pas le choix optimal.
même si ce n'est pas le choix optimal.
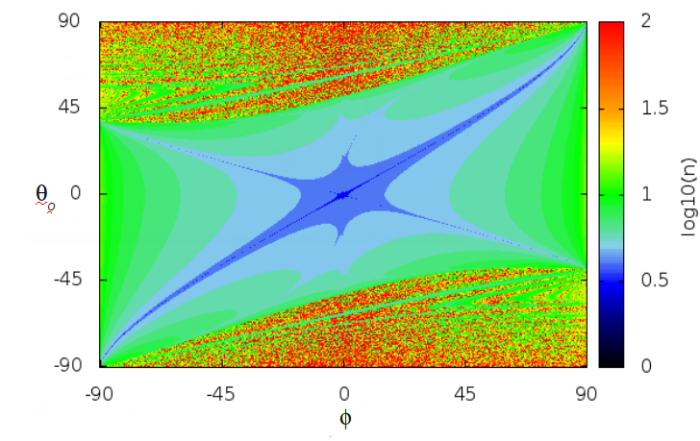
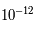 sur
sur 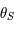 en fonction de
en fonction de 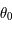 et
et 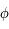 .
.
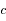 correspond à la vitesse de la lumière dans le vide,
correspond à la vitesse de la lumière dans le vide, 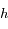 est la constante de Planck,
est la constante de Planck, 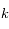 la constante de Boltzmann,
la constante de Boltzmann, 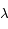 la longueur d'onde à laquelle le rayonnement est émis et
la longueur d'onde à laquelle le rayonnement est émis et 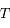 la température de surface du corps noir.
la température de surface du corps noir.
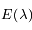 pour différentes températures de surface du corps noir. On peut remarquer que le maximum de la courbe se déplace sur la gauche lorsque la température augmente. Autrement dit, la longueur d'onde pour laquelle le rayonnement émis est maximal diminue lorsque la température de surface augmente.
pour différentes températures de surface du corps noir. On peut remarquer que le maximum de la courbe se déplace sur la gauche lorsque la température augmente. Autrement dit, la longueur d'onde pour laquelle le rayonnement émis est maximal diminue lorsque la température de surface augmente.

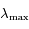 et
et 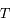 .
.
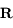 , mais ce théorème peut être admis ici.
, mais ce théorème peut être admis ici.
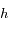 ,
, 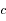 et
et 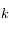 sont des constantes strictement positives et que la température
sont des constantes strictement positives et que la température 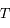 étant mesurée en Kelvin est aussi strictement positive, montrer que
étant mesurée en Kelvin est aussi strictement positive, montrer que 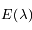 est de classe
est de classe 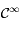 sur
sur ![]0,+\infty[](../pages_extremas/equations_extremas/equation17.png) et est toujours strictement positive sur cet intervalle.
et est toujours strictement positive sur cet intervalle.
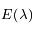 quand
quand 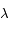 tend vers 0 et vers
tend vers 0 et vers 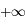 sont toutes les deux égales à zéro. Ce résultat peut être admis ici.
sont toutes les deux égales à zéro. Ce résultat peut être admis ici.
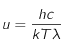 . Pour la limite en
. Pour la limite en 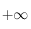 on pourra faire un dévelopement limité en 0 à l'ordre 1 de la fonction exponentielle.
on pourra faire un dévelopement limité en 0 à l'ordre 1 de la fonction exponentielle.
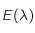 sur
sur 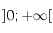 .
.
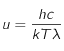 , montrer qu'étudier le signe de
, montrer qu'étudier le signe de 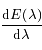
 revient à étudier celui de
revient à étudier celui de 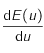 .
.
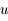 , de la forme
, de la forme 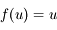 , pour que
, pour que 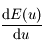 s'annule. On note
s'annule. On note 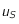 la solution de cette équation lorsqu'elle existe.
la solution de cette équation lorsqu'elle existe.
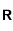 que
que 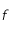 admet un point fixe et que la suite définie par
admet un point fixe et que la suite définie par 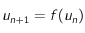 converge vers ce point fixe (voir
converge vers ce point fixe (voir 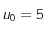 trouver une valeur
trouver une valeur 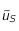 qui soit une valeur approchée de
qui soit une valeur approchée de 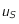 à
à 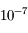 prêt.
prêt.
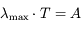 où
où 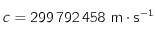 ,
, 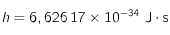 et
et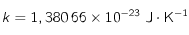 . Cette relation correspond à la loi du déplacement de Wien pour les corps noirs.
Justifier l'utilisation de
. Cette relation correspond à la loi du déplacement de Wien pour les corps noirs.
Justifier l'utilisation de 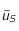 dans le calcul de la constante
dans le calcul de la constante 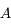 .
.
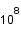 K.
Le but de cet exercice est de déterminer grâce à un modèle simple le rayon d'équilibre de ces étoiles.
K.
Le but de cet exercice est de déterminer grâce à un modèle simple le rayon d'équilibre de ces étoiles.
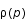 est la suivante:
est la suivante: 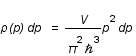 , où V est le volume et
, où V est le volume et 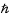 la constante de Planck réduite.
la constante de Planck réduite.
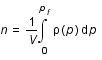 où
où 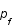 est l'impulsion de Fermi, c'est à dire l'impulsion maximale.
Exprimer n en fonction de
est l'impulsion de Fermi, c'est à dire l'impulsion maximale.
Exprimer n en fonction de 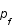 .
.
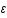 :
:
 .
calculer
.
calculer  en fonction de
en fonction de  .
.
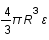 , l'exprimer en fonction de l'impulsion de Fermi puis en fonction des caractéristiques de l'étoile et de la masse du neutron.
, l'exprimer en fonction de l'impulsion de Fermi puis en fonction des caractéristiques de l'étoile et de la masse du neutron.
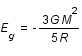 , où G est la constante de gravitation. L'équilibre est atteint lorsque l'énergie totale (celle du gaz plus celle gravitationnelle) de l'étoile est minimum. Calculer le rayon
, où G est la constante de gravitation. L'équilibre est atteint lorsque l'énergie totale (celle du gaz plus celle gravitationnelle) de l'étoile est minimum. Calculer le rayon 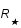 qui minimise l'énergie en fonction de la masse de l'étoile et des constantes m, G et
qui minimise l'énergie en fonction de la masse de l'étoile et des constantes m, G et 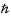 . Calculer ce rayon pour le soleil.
. Calculer ce rayon pour le soleil.
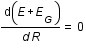 .
.
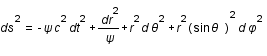 , où
, où 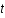 est le temps,c la vitesse de la lumière,
est le temps,c la vitesse de la lumière, 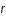
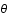
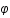 sont les coordonnées sphériques et
sont les coordonnées sphériques et 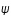 est défini comme
est défini comme 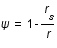 . Le rayon de Schwarzschild
. Le rayon de Schwarzschild 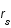 est directement relié à la masse du corps central par
est directement relié à la masse du corps central par 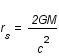 , où G est la constante de gravitation.
, où G est la constante de gravitation.
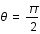 . Que vaut
. Que vaut 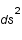 dans le cas d'une orbite circulaire ?
dans le cas d'une orbite circulaire ?
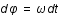 , où
, où 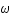 est la fréquence angulaire du mouvement vu par un observateur lointain. Sachant que pour qu'un mouvement soit physiquement réalisable il faut que
est la fréquence angulaire du mouvement vu par un observateur lointain. Sachant que pour qu'un mouvement soit physiquement réalisable il faut que 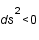 (ceci vient uniquement d'un choix spécifique de métrique); déterminer la condition sur
(ceci vient uniquement d'un choix spécifique de métrique); déterminer la condition sur 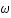 .
.
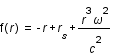
 . Que vaut son rayon ?
. Que vaut son rayon ?
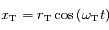
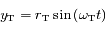 .
.
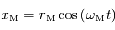
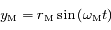 .
.
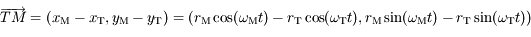 .
.
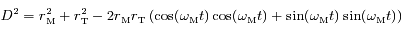
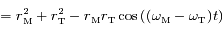 ,
,
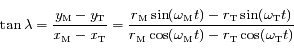 . Cette fonction n'est pas définie lorsque
. Cette fonction n'est pas définie lorsque 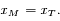
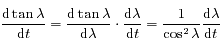 .
.
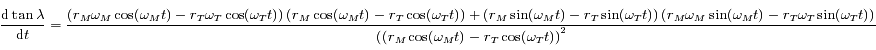
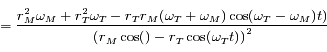 .
.
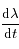 est celui du numérateur de l'expression ci-dessus.
Ainsi, quand
est celui du numérateur de l'expression ci-dessus.
Ainsi, quand 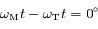 , le signe de la dérivée est celui de
, le signe de la dérivée est celui de 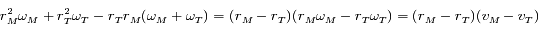 ,
oùt
,
oùt 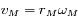 et
et 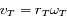 .
.
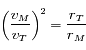 . Ainsi, pour Mars on a
. Ainsi, pour Mars on a 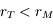 et
et 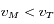 , donc la dérivée est négative.
De même on montre que pour
, donc la dérivée est négative.
De même on montre que pour 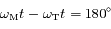 , la dérivée est positive.
, la dérivée est positive.
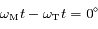 ), le mouvement de Mars est rétrograde, alors qu'à la
), le mouvement de Mars est rétrograde, alors qu'à la 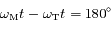 , le mouvement est prograde.
, le mouvement est prograde.
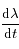 s'annulle lorsque
s'annulle lorsque 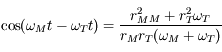 , soit
, soit 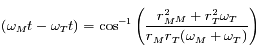 .
.
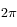 près, deux solutions opposées l'une de l'autre.
près, deux solutions opposées l'une de l'autre.
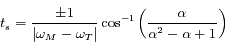 , d'où la durée de la rétrogradation
, d'où la durée de la rétrogradation 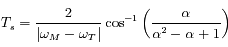 .
.
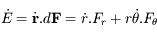 et
et 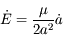 , où
, où 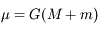 .
.
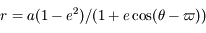 ,
, 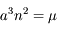 donc
donc 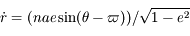 et
et ![r {\dot \theta} = (na [1 + e \cos(\theta - \varpi) ]) / \sqrt{1 - e^2}](../pages_def/equations_def/equation77.png) .
.
![{\dot a} = 2 a^{\displaystyle 3/2} [F_r e \sin (\theta - \varpi) + F_\theta (1 + e \cos (\theta - \varpi)) ]/\sqrt{\mu(1-e^2)}](../pages_def/equations_def/equation78.png)
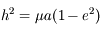 ,
, 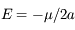 , donc
, donc 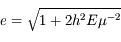 et
et 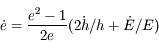 .
.
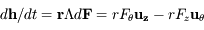 donc
donc 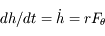
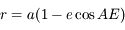 où
où 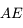 est l'
est l'![{\dot e} = \sqrt{a(1-e^2)/\mu}[F_r \sin(\theta - \varpi) + F_\theta (\cos (\theta-\varpi) + \cos AE]](../pages_def/equations_def/equation90.png) .
.
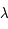 et
et 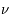 sont égales, elles donnent toutes deux la luminance intégrale du corps noir (
sont égales, elles donnent toutes deux la luminance intégrale du corps noir (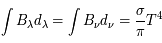
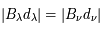 où
où 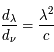
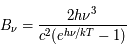 (donné couramment en
(donné couramment en 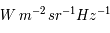 )
)


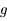 . Cette racine est unique car
. Cette racine est unique car 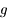 est croissant. On dresse alors le tableau de variation de
est croissant. On dresse alors le tableau de variation de 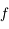 et comme
et comme 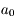 est négatif, de la même manière, il n'y a qu'une seule racine positive. Ce qui n'est pas notre cas.
est négatif, de la même manière, il n'y a qu'une seule racine positive. Ce qui n'est pas notre cas.
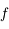 sur l'intervalle définie par ses 2 racines positives indique que
sur l'intervalle définie par ses 2 racines positives indique que 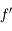 s'annule en un point
s'annule en un point 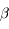 distint des 2 racines de
distint des 2 racines de 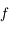 .
. 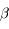 est donc positif non nul. Or
est donc positif non nul. Or 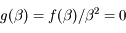
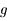 qui normalement a déjà été fait.
qui normalement a déjà été fait.
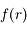 dans
dans ![\mathbb{C} [X]](../pages_af/equations_af/equation48.png) , le polynôme a 8 racines complexes. On en déduit que
, le polynôme a 8 racines complexes. On en déduit que 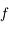 admet aussi 4 racines complexes non réelles.
admet aussi 4 racines complexes non réelles.
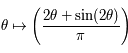 est continue dérivable et strictement croissante. Ainsi l'image de
est continue dérivable et strictement croissante. Ainsi l'image de 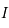 est l'ensemble
est l'ensemble ![[-1, 1]](../pages_af/equations_af/equation129.png) .
Donc la fonction
.
Donc la fonction  est bien définie sur
est bien définie sur 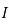 .
.
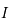 est symétrique par rapport à zéro,
est symétrique par rapport à zéro, 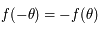 . Donc
. Donc 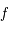 est une fonction impaire sur
est une fonction impaire sur 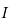 .
.
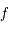 est dérivable sur
est dérivable sur ![]-\pi/2, \pi/2[](../pages_af/equations_af/equation143.png) par composition de fonction continues et dérivables.
On a:
par composition de fonction continues et dérivables.
On a:
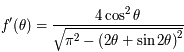 .
.
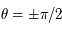 . On pose alors
. On pose alors 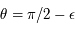 . Ainsi:
. Ainsi:
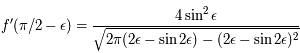 .
.
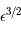 alors que le numérateur est de l'ordre de
alors que le numérateur est de l'ordre de 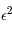 . Ainsi on a:
. Ainsi on a: 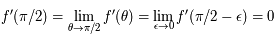 . Comme
. Comme 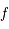 est impaire on a de même en prolongeant par continuité
est impaire on a de même en prolongeant par continuité 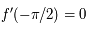 .
.
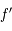 est strictement supérieur à zéro sur
est strictement supérieur à zéro sur ![]-\pi/2, \pi/2[](../pages_af/equations_af/equation159.png) , et ne s'annule qu'en
, et ne s'annule qu'en 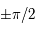 .
Ainsi
.
Ainsi 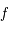 est strictement croissante sur
est strictement croissante sur 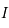 . Comme
. Comme 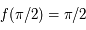 , par parité on en déduit que
, par parité on en déduit que 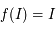 .
Donc
.
Donc 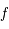 est une fonction bijective de
est une fonction bijective de 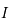 dans lui-même. Il existe donc une fonction réciproque
dans lui-même. Il existe donc une fonction réciproque 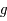 .
D'après les propriétés de
.
D'après les propriétés de 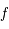 , on en déduit que
, on en déduit que 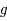 est une fonction impaire définie et continue sur
est une fonction impaire définie et continue sur 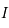 et dérivable sur
et dérivable sur 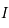 ouvert.
De plus comme on a
ouvert.
De plus comme on a ![f([0,\pi/2])=[0,\pi/2]](../pages_af/equations_af/equation172.png) , on a aussi
, on a aussi ![g([0,\pi/2])=[0,\pi/2]](../pages_af/equations_af/equation173.png) .
.
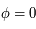 , alors l'équation (*) admet
, alors l'équation (*) admet 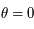 comme solution (en effet
comme solution (en effet 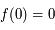 , c'est-à-dire
, c'est-à-dire 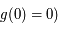 . Ainsi
. Ainsi 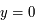 et
et 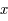 varie de
varie de 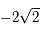 à
à 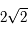 lorsque
lorsque 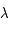 varie de
varie de 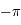 à
à 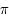 .
. 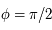 . Or
. Or 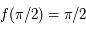 , soit
, soit 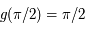 , ainsi
, ainsi 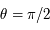 . L'image du pôle nord est
. L'image du pôle nord est 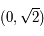 .
Par symétrie, le pôle Sud a pour image
.
Par symétrie, le pôle Sud a pour image 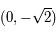 .
. 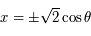 et
et 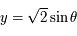 (le signe "+" correspond à la longitude positive). Les points se trouvent donc sur un demi-cercle centré à l'origine et de rayon
(le signe "+" correspond à la longitude positive). Les points se trouvent donc sur un demi-cercle centré à l'origine et de rayon 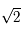 se trouvant à droite de l'axe des ordonnées pour la longitude positive et à gauche pour la longitude négative. Comme un méridien correspond à l'ensemble des latitudes
se trouvant à droite de l'axe des ordonnées pour la longitude positive et à gauche pour la longitude négative. Comme un méridien correspond à l'ensemble des latitudes ![\phi \in [-\pi/2,\pi/2]](../pages_af/equations_af/equation199.png) , chaque demi-cercle est décrit complètement d'après la propriété de la fonction
, chaque demi-cercle est décrit complètement d'après la propriété de la fonction 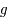 :
: ![g([-\pi/2,\pi/2])=[-\pi/2,\pi/2]](../pages_af/equations_af/equation201.png) .
.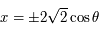 et
et 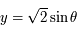 . Comme à la question précédente sauf que les points se trouvent sur deux demi-ellipses d'une ellipse centrée à l'origine et de demi-petit axe
. Comme à la question précédente sauf que les points se trouvent sur deux demi-ellipses d'une ellipse centrée à l'origine et de demi-petit axe 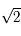 parallèle à l'axe des ordonnées et de demi-grand axe
parallèle à l'axe des ordonnées et de demi-grand axe 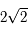 . Toute l'ellipse est décrite, pour la même raison que précédemment.
. Toute l'ellipse est décrite, pour la même raison que précédemment. 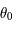 la solution de l'équation (*) pour la latitude
la solution de l'équation (*) pour la latitude 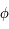 , i.e.
, i.e. 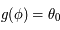 , alors
, alors 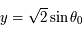 et
et 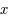 varie de
varie de 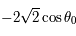 à
à 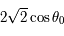 lorsque
lorsque 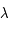 varie de
varie de 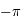 à
à 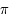 . C'est une corde de l'ellipse parallèle à l'axe des abcisses.
. C'est une corde de l'ellipse parallèle à l'axe des abcisses. , or
, or 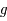 est impaire, donc
est impaire, donc 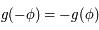 , ce qui répond au premier point. Ensuite, comme
, ce qui répond au premier point. Ensuite, comme ![g([0,\pi/2])=[0,\pi/2]](../pages_af/equations_af/equation232.png) on en déduit que si
on en déduit que si ![\phi\in[0,\pi/2]](../pages_af/equations_af/equation233.png) alors la solution de
alors la solution de 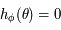 est dans
est dans ![[0,\pi/2]](../pages_af/equations_af/equation235.png) . Les deux dernières égalités viennent directement du fait que
. Les deux dernières égalités viennent directement du fait que 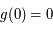 et
et 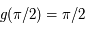 .
.
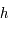 est définie continue dérivable sur
est définie continue dérivable sur 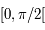 comme composée de fonctions définies continues et dérivables. On a
comme composée de fonctions définies continues et dérivables. On a 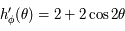 qui est continue et strictement positive sur
qui est continue et strictement positive sur 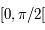 . Elle est aussi dérivable, avec
. Elle est aussi dérivable, avec 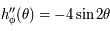 .
. 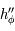 est strictement négative sur
est strictement négative sur ![]0,\pi/2[](../pages_af/equations_af/equation251.png) et nulle en 0. Ainsi
et nulle en 0. Ainsi 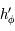 est strictement décroissante sur
est strictement décroissante sur 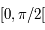 .
.
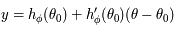 . Pour
. Pour 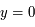 on obtient
on obtient 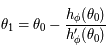 .
Comme
.
Comme 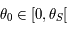 , que
, que 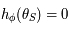 et que
et que 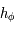 est croissante, on en déduit que
est croissante, on en déduit que 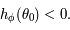 De plus
De plus 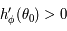 ainsi
on a bien
ainsi
on a bien 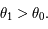 D'après le théorème des accroissements finis, il existe
D'après le théorème des accroissements finis, il existe ![\theta\in]\theta_0,\theta_S[](../pages_af/equations_af/equation275.png) tel que
tel que 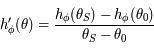 . Ainsi, en considérant
. Ainsi, en considérant 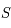 comme le point d'intersection entre l'axe des abscisses et la droite passant par
comme le point d'intersection entre l'axe des abscisses et la droite passant par 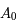 et de coefficient directeur
et de coefficient directeur 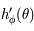 , on a
, on a 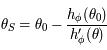 . Comme
. Comme 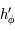 est une fonction strictement décroissante sur
est une fonction strictement décroissante sur ![]\theta_0, \theta_S[](../pages_af/equations_af/equation282.png) , on en déduit que
, on en déduit que 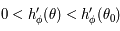 , soit
, soit 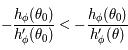 .
Ainsi on a bien
.
Ainsi on a bien 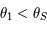 .
.
![\phi\in]0,\pi/2[](../pages_af/equations_af/equation300.png) alors
alors ![\theta_S\in]0,\pi/2[](../pages_af/equations_af/equation301.png) . Autrement dit
. Autrement dit 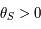 , donc
, donc 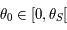 . Ainsi d'après la question précédente on sait que
. Ainsi d'après la question précédente on sait que 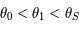 . Donc
. Donc 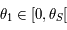 .
Si on suppose maintenant
.
Si on suppose maintenant 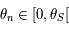 alors, toujours d'après la question précédente on a
alors, toujours d'après la question précédente on a 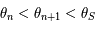 , en outre
, en outre 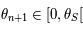 .
Ainsi,
.
Ainsi, 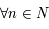 on a
on a 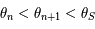 . Donc la suite
. Donc la suite 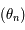 est croissante et majorée, donc elle converge vers une limite
est croissante et majorée, donc elle converge vers une limite 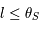 .
Par continuité de
.
Par continuité de 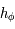 et
et 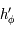 , on a
, on a 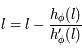 , et comme
, et comme 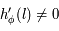 , on en déduit que
, on en déduit que 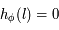 , donc
, donc 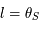 .
.
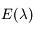 s'écrit comme un produit et composition de fonction de classe
s'écrit comme un produit et composition de fonction de classe 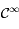 sur leur ensemble de définition. Ainsi
sur leur ensemble de définition. Ainsi 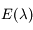 est de classe
est de classe 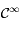 sur son intervalle de définition, c'est à dire sur
sur son intervalle de définition, c'est à dire sur ![]0,+\infty[](../pages_extremas/equations_extremas/equation22.png) .
.
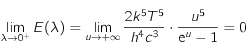 car l'exponentielle l'emporte sur tout polynôme en
car l'exponentielle l'emporte sur tout polynôme en 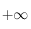 .
.
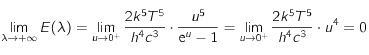 où on a utilisé le dévelopement limité en 0 à l'ordre 1 de la fonction exponentielle :
où on a utilisé le dévelopement limité en 0 à l'ordre 1 de la fonction exponentielle :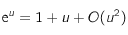 .
.
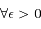 ,
, 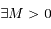 et
et 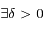 tels que
tels que 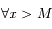 on a
on a 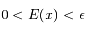 et
et 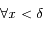 et
et 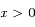 on a
on a 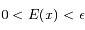 .
.
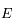 est une fonction continue sur l'intervalle
est une fonction continue sur l'intervalle ![[\delta,M]](../pages_extremas/equations_extremas/equation43.png) . Or l'image d'un segment fermé par une fonction continue est un segment fermé. Ce dernier possède donc une borne supérieure qui est atteinte par la fonction
. Or l'image d'un segment fermé par une fonction continue est un segment fermé. Ce dernier possède donc une borne supérieure qui est atteinte par la fonction 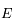 sur
sur ![[\delta,M]](../pages_extremas/equations_extremas/equation45.png) .
.
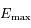 ce maximum. On peut alors choisir
ce maximum. On peut alors choisir 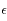 pour que
pour que 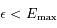 , ainsi
, ainsi 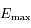 sera aussi le maximum de
sera aussi le maximum de 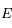 sur
sur ![]0,+\infty[](../pages_extremas/equations_extremas/equation51.png) .
.
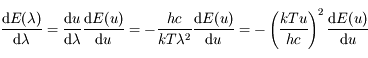 ,
,
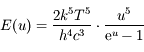 donc
donc 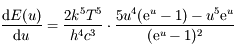 .
.
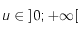 , et que
, et que 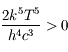 on a
on a 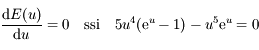 .
.
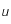 peut se mettre sous la forme
peut se mettre sous la forme 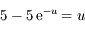 .
.
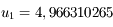
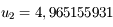
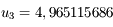
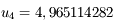
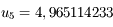
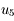 est une approximation qui répond à la question.
est une approximation qui répond à la question.
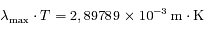 .
.
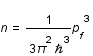
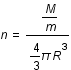
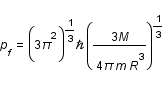
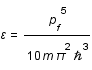
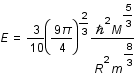
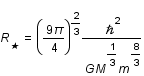 L'application numérique donne pour une étoile d'une masse solaire un rayon de 12km !
L'application numérique donne pour une étoile d'une masse solaire un rayon de 12km !
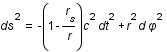
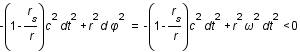
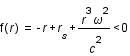
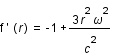
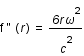 La dérivée seconde est toujours positive, la fonction est donc convexe. Son minimum est atteint en
La dérivée seconde est toujours positive, la fonction est donc convexe. Son minimum est atteint en 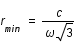 lorsque la dérivé s'annule. Lorsque
lorsque la dérivé s'annule. Lorsque 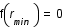 , il n'y a plus de solution possible donc
, il n'y a plus de solution possible donc 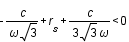 soit
soit 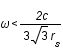
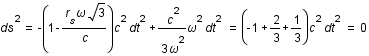
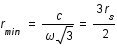 Ce rayon correspond à la dernière orbite possible pour des photons c'est la sphère photonique.
Ce rayon correspond à la dernière orbite possible pour des photons c'est la sphère photonique.