Fonctions de plusieurs variables
- Introduction
- Dérivations partielles
- Entropie
- Ex: Entropie
- Formulation hamiltonienne du problème de 2 corps
- Ex: Formulation hamiltonienne du problème de 2 corps
- Les variables de Delaunay
- Ex: les variables de Delaunay
- Théorème d'inversion de Lagrange
- Ex: Théorème d'inversion de Lagrange
- Paramètre de Tisserand
- Ex: paramètre de Tisserand
- Intégrales multiples
- Photométrie des surfaces planétaires
- Ex: photométrie des surfaces planétaires
- Théorème de Liouville
- Ex: théorème de Liouville
Introduction
On trouvera dans ce chapitre les exercices suivants :
- Détermination de l'entropie de l'univers en fonction de sa température (dérivations partielles)
- Formulation hamiltonienne du problème des deux corps (dérivations partielles)
- Variables de Delaunay dans le problème des deux corps (dérivations partielles)
- Théorème d'inversion de Lagrange (dérivations partielles)
- Paramètre de Tisserand (dérivations partielles)
- Photométrie planétaire (intégrales multiples)
- Théorème de Liouville (intégrales multiples)
Dérivations partielles
Auteurs: Jérôme Thiébaut, Marc Fouchard, S. Renner
Entropie
Auteur : Jérôme Thiébaut
La connaissance du contenu de l'univers en terme de particules et d'énergie est indispensable à la compréhension de son évolution. Juste après le Big Bang, l'univers était très chaud et les premières particules présentes n'étaient ni des électrons ni des protons, mais plutôt des quarks, neutrinos... En se diluant, l'univers refroidit et les particules qui le constituent changent et évoluent ensemble puis séparément. La température de l'univers est donc une quantité extrêmement importante.
La thermodynamique est la branche de la physique qui permet de traiter ce problème. Elle permet, grâce à ses lois, de relier entre elles diverses quantités fondamentales telles que la température, la pression, l'énergie, la densité de particules, de photons...
L'entropie est une de ces quantités. Elle mesure en quelque sorte le degré de désordre d'un système microscopique, où autrement dit, la capacité d'un système de particules à produire ou non des phénomènes collectifs.
Le but de cet exercice est d'exprimer l'entropie en fonction de la température de l'univers.
Ex: Entropie
Auteur: Jérôme Thiébaut
 Entropie
Entropie
Difficulté : ☆
Temps : 10 min
On peut relier la variation d'énergie, 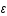 , aux variations d'entropie, S, et de volume, V, par la relation suivante:
, aux variations d'entropie, S, et de volume, V, par la relation suivante:
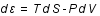 ,
où T est la température et P la pression.
,
où T est la température et P la pression.
Question 1)
Exprimer la variation d'entropie en fonction des variations de volume et de densité volumique d'énergie, 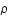 .
.
Question 2)
Exprimer la variation d'entropie en fonction des variations de volume et de température.
Question 3)
Montrer que 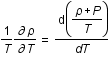 .
.
Utiliser la propriété suivante: 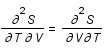 .
.
Question 4)
Exprimer la variation d'entropie comme la variaton d'une seule quantité dépendant de V, P, T et 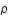 puis relier l'entropie à ces variables thermodynamiques.
puis relier l'entropie à ces variables thermodynamiques.
Formulation hamiltonienne du problème de 2 corps
Auteur : Marc Fouchard
On a vu dans cet exercice comment résoudre le problème de deux corps.
Nous allons voir ici, comment obtenir les équations hamiltoniennes de ce problème.
On considère donc un corps ponctuel 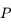 de masse unité mobile dans un plan et soumis à l'attraction gravitationnelle d'un corps fixe de masse
de masse unité mobile dans un plan et soumis à l'attraction gravitationnelle d'un corps fixe de masse 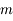 se trouvant en
se trouvant en 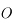 . On suppose que
. On suppose que 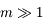 .
.
Ex: Formulation hamiltonienne du problème de 2 corps
Auteur: Marc Fouchard
 Formulation hamiltonienne du problème de 2 corps
Formulation hamiltonienne du problème de 2 corps
Difficulté : ☆
Temps : 30 mn
Question 1)
On se place dans un repère polaire, centré sur 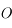 . On précise que la force universelle de la gravitation
s'appliquant au point
. On précise que la force universelle de la gravitation
s'appliquant au point 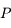 est:
est:
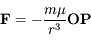 ,
,
où 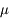 désigne la constante universelle de la gravitation et
désigne la constante universelle de la gravitation et 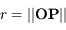 (les notations en gras dénotent des vecteurs).
(les notations en gras dénotent des vecteurs).
Déterminer le potentiel dont dérive la force. En déduire l'énérgie potentielle 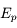 .
.
Question 2)
Calculer l'énergie cinétique. En déduire le lagrangien et le hamiltonien du système.
Question 4)
En déduire les équations hamiltoniennes du problème.
Pour chaque couple 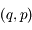 on a les équations:
on a les équations:
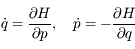 .
.
Les variables de Delaunay
Auteur: Marc Fouchard
On a vu dans l'exercice sur la formulation hamiltonienne du problème de 2 corps, comment écrire les équations de hamilton de ce problème. Cependant, on n'intégrait pas les équations. On va voir ici, qu'en utilisant des variables hamiltoniennes appropriées on peut intégrer le problème très facilement. Ces variables sont les variables de Delaunay.
Ex: les variables de Delaunay
Auteur: Marc Fouchard
 Les variables de Delaunay
Les variables de Delaunay
Difficulté : ☆
Temps : 10 mn
Théorème d'inversion de Lagrange
Auteur: S. Renner
Le théorème d'inversion de Lagrange donne le développement en série d'une fonction définie implicitement. L'application de ce théorème permet entre autres d'obtenir une solution numérique de l'équation de Kepler 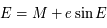 , ou d'écrire des développements utiles du problème des deux corps.
, ou d'écrire des développements utiles du problème des deux corps.
Voici un énoncé de ce théorème :
Soit 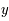 fonction de 2 variables
fonction de 2 variables 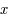 et
et 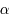 et d'une fonction
et d'une fonction 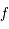 infiniment dérivable de la forme :
infiniment dérivable de la forme : 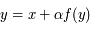 avec
avec 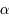 petit.
petit.
Alors 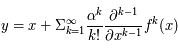 .
.
On propose ici de le démontrer par une méthode reposant sur les dérivées partielles, révélée par Pierre-Simon Laplace.
Ex: Théorème d'inversion de Lagrange
Auteur: S. Renner
 Théorème d'inversion de Lagrange
Théorème d'inversion de Lagrange
Difficulté : ☆☆
Temps : 1H
On va donc démontrer que si 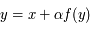 , alors
, alors 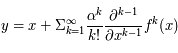 avec
avec 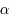 petit.
petit.
Question 1)
Développer 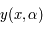 au voisinage de
au voisinage de 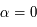 .
.
Question 2)
Montrer que 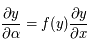 .
.
Question 3)
Montrer que pour tout entier 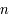 strictement positif,
strictement positif, 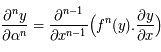 . On utilisera le résultat de la question précédente.
. On utilisera le résultat de la question précédente.
Question 4)
En déduire 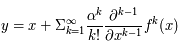 .
.
Paramètre de Tisserand
Auteur: Marc Fouchard
Date de création: 9 Mai 2013
L'objectif de cet exercice est de déterminer le paramètre de Tisserand qui est une quasi-constante du mouvement pour les comètes observées.
Ainsi ce paramètre permet de montrer que l'observation de deux comètes à des époques différentes correspondent en fait au même objet.
Ex: paramètre de Tisserand
Auteur: Marc Fouchard
 Paramètre de Tisserand
Paramètre de Tisserand
Difficulté : ☆
Temps : 1h30
On considère un problème de trois corps où les deux premiers 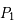 et
et 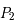 , appelés primaires et de masse respective
, appelés primaires et de masse respective 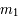 et
et 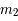 , sont sur des orbites circulaires et uniforme ; et le troisième
, sont sur des orbites circulaires et uniforme ; et le troisième 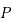 , de masse
négligeable voit sa trajectoire affectée
par les primaires alors que celui-ci n'affecte pas le mouvement des deux primaires. Ce problème est appelé le problème de trois corps restreint et circulaire.
, de masse
négligeable voit sa trajectoire affectée
par les primaires alors que celui-ci n'affecte pas le mouvement des deux primaires. Ce problème est appelé le problème de trois corps restreint et circulaire.
On considère un repère tournant orthonormé, centré sur le centre de gravité 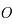 des deux primaires et dont les axes sont tels que l'axe des abscisses est dirigé vers le deuxième primaire, l'axe des ordonnées fait un angle de
des deux primaires et dont les axes sont tels que l'axe des abscisses est dirigé vers le deuxième primaire, l'axe des ordonnées fait un angle de 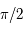 avec celui des abscisse dans le même sens que le mouvement de rotation des primaires, et l'axe des
avec celui des abscisse dans le même sens que le mouvement de rotation des primaires, et l'axe des 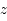 complète un trièdre direct.
complète un trièdre direct.
On considère aussi un repère fixe orthonormé qui coïncide avec le repère tournant à 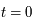 .
.
Dans le repère tournant, les coordonnées des deux primaires sont 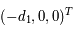 et
et 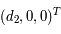 , où
, où 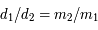 et
et 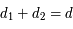 qui est la distance (fixe) qui sépare les deux primaires. On note
qui est la distance (fixe) qui sépare les deux primaires. On note 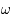 la vitesse de rotation angulaire des deux primaires par rapport au repère fixe.
la vitesse de rotation angulaire des deux primaires par rapport au repère fixe.
De manière générale on notera 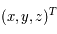 les coordonnées dans le repère fixe et
les coordonnées dans le repère fixe et 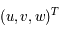 les coordonnées dans le repère tournant.
Le point au dessus d'une quantité indique la dérivée par rapport au temps de cette quantité.
les coordonnées dans le repère tournant.
Le point au dessus d'une quantité indique la dérivée par rapport au temps de cette quantité.
Question 2)
Déterminer les formules de passage entre 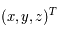 et
et 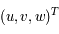 pour un même objet.
pour un même objet.
Question 4)
En différenciant les expressions de 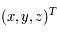 en fonction de
en fonction de 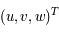 , en déduire les équations du mouvement dans le repère tournant.
, en déduire les équations du mouvement dans le repère tournant.
Question 5)
Montrer qu'il existe une fonction 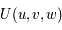 tel que le système d'équations précédent s'écrit :
tel que le système d'équations précédent s'écrit :
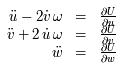 ,
,
Question 6)
En multipliant chaque ligne du système précédent par 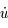 ,
, 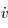 et
et 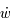 respectivement, puis en additionnant, montrer que le système admet une intégrale du mouvement (c'est -à-dire une quantité qui est constante au cours du temps).
respectivement, puis en additionnant, montrer que le système admet une intégrale du mouvement (c'est -à-dire une quantité qui est constante au cours du temps).
Question 7)
En déduire 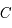 en fonction de
en fonction de 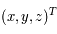 et de leur dérivées par rapport au temps.
et de leur dérivées par rapport au temps.
Intégrales multiples
Auteurs: Stéphane Erard, Marc Fouchard
Photométrie des surfaces planétaires
Les surfaces planétaires réfléchissent la lumière solaire d'une façon qui dépend de leurs propriétés et de leur composition. Si les caractéristiques spectrales reflètent la composition (minéralogique) d'une surface, la distribution angulaire du rayonnement diffusé dépend surtout de ses propriétés physiques : taille de particules, porosité, rugosité à diverses échelles...
Divers modèles photométriques rendent compte de ces comportements, en décrivant la dépendance angulaire de la luminance. La luminance est la puissance émise ou diffusée dans un angle solide élémentaire par unité de surface. Il s’agit d’une caractéristique intrinsèque à la source lumineuse :
Figure 1
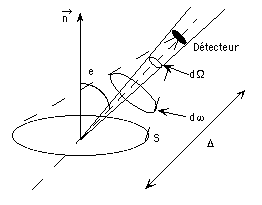
Géométrie d'observation d'une surface
Dans la configuration générale décrite Figure 1, la luminance est définie de la façon suivante :
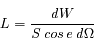
où dW est la puissance recueillie par le détecteur, e est l'angle sous lequel on voit la source, 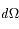 l'angle solide sous lequel la source voit le détecteur, et S la surface de la source. Dans le Système International, la luminance se mesure en
l'angle solide sous lequel la source voit le détecteur, et S la surface de la source. Dans le Système International, la luminance se mesure en 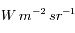 , ou dans un intervalle de longueur d'onde élémentaire en
, ou dans un intervalle de longueur d'onde élémentaire en 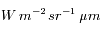 .
.
Le modèle photométrique le plus commun est le modèle lambertien, que suit notamment le corps noir : la luminance est simplement isotrope (ne dépend pas de la direction e).
Ex: photométrie des surfaces planétaires
 Soleil
Soleil
Difficulté : ☆☆
Temps : 45 min
Question 1)
On assimile le Soleil à un corps noir. Quelle est la puissance rayonnée par un élément de surface dans une direction donnée ?
En première approximation, le Soleil rayonne comme un corps noir à la température de la photosphère (5780 K en moyenne).
Question 2)
Calculer la luminance intégrale (intégrée spectralement), toujours dans une direction donnée. Application numérique.
Question 3)
Calculer la luminosité totale d'un élément de surface (rayonnée dans toutes les directions). Commenter.
Question 4)
Calculer la puissance totale émise par le Soleil. Application numérique (on donne pour le rayon du Soleil 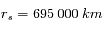 ).
).
 Surface lunaire
Surface lunaire
Difficulté : ☆☆
Temps : 20 min
Le cas des surfaces planétaires est différent, leur capacité à réfléchir le rayonnement solaire dépendant de leur état physique : rugosité, taille des particules en surface... En outre la position du Soleil intervient également puisqu'on observe maintenant en réflexion (voir Figure 2). Le modèle lambertien est encore adapté aux surfaces très claires, mais ne décrit pas correctement les propriétés de la Lune ou des astéroïdes qui sont relativement sombres. On utilise souvent le modèle de Lommel-Seeliger, qui donne la luminance comme :
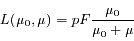
où p est l'albedo de la surface (coefficient de réflexion sous incidence et émergence nulles), F est le flux solaire à la distance de la planète, 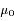 et
et 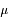 sont les cosinus des angles d'incidence et d'émergence.
sont les cosinus des angles d'incidence et d'émergence.
Figure 2
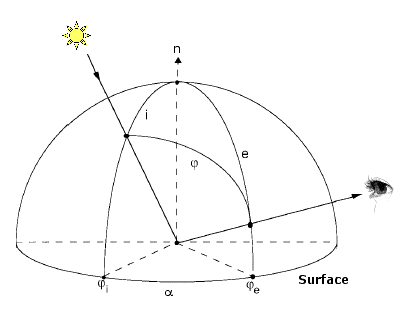
Géométrie d'observation d'une surface planétaire
Question 1)
On utilise la réflectance hémisphérique pour étudier les propriétés thermiques des surfaces. Celle-ci est définie comme :
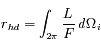
où 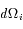 est l'angle solide élémentaire dans la direction d'incidence.
est l'angle solide élémentaire dans la direction d'incidence.
Calculer cette quantité en fonction des variables 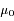 et
et 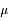 .
.
Théorème de Liouville
Auteur : Marc Fouchard.
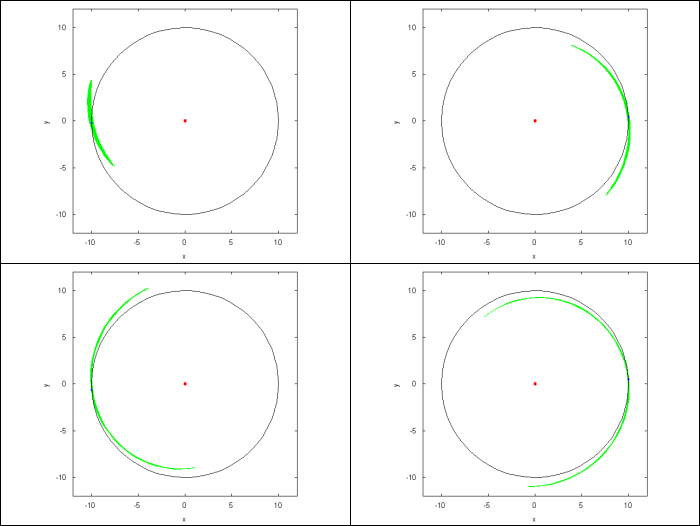
Le but de cet exercice est de montrer qu'un volume soumis à un flux, c'est-à-dire qu'en chaque point de l'espace on peut associer un vecteur vitesse donné par une équation différentielle d'ordre 1, hamiltonien reste constant.
La figure suivante illustre cette propriété dans le cas du problème de 2 corps plan. Comme on est à deux dimensions un volume correspond à une surface. Le disque est soumis à une force gravitationelle due à un corps massif se trouvant à l'origine. La surface verte est constante au cours du temps, même si la forme est fortement modifiée.
théorème de Liouville
Un flux hamiltonien vérifie les équations d'hamilton. C'est-à-dire que le point de coordonnées 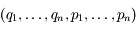 vérifie les équations différentielles suivantes :
vérifie les équations différentielles suivantes :
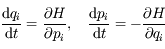 , avec
, avec 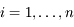 .
.
où 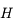 est le hamiltonien du système, indépendant du temps.
est le hamiltonien du système, indépendant du temps.
Ex: théorème de Liouville
Auteur: Marc Fouchard
 théorème de Liouville
théorème de Liouville
Difficulté : ☆☆☆
Temps : 1h
Question 2)
Montrer que 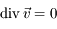 et donc que
et donc que 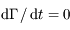 .
.
Réponses aux exercices
pages_der-part/ent-exo.html
Exercice
'Entropie'
-
Question 1
Aide :
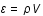
Solution :
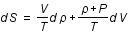
-
Question 2
Aide :
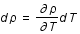
Solution :
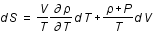
-
Question 3
Aide :
Utiliser la propriété suivante: 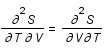 .
.
Solution :
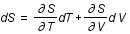
donc 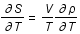 et
et 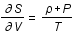 .
.
Comme 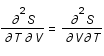 ,
, 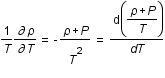
-
Question 4
Solution :
Avec l'égalité de l'équation précédente, il vient: 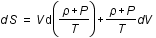 .
Donc,
.
Donc, 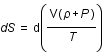 et
et 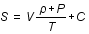 , où C est une constante d'intégration.
, où C est une constante d'intégration.
-
Question 5
Solution :
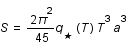
L'entropie étant constante, 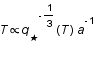 .
.
pages_der-part/exo-pb-2corps-hami.html
Exercice
'Formulation hamiltonienne du problème de 2 corps'
pages_der-part/exo-delaunay.html
Exercice
'Les variables de Delaunay'
pages_der-part/exo-th-inversion-lagrange-der-part.html
Exercice
'Théorème d'inversion de Lagrange'
pages_der-part/exo-tisserand.html
Exercice
'Paramètre de Tisserand'
-
Question 1
Solution :
on a le système d'équation suivant :
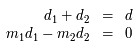 .
.
Ce qui nous donne :
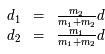 .
.
-
Question 2
Solution :
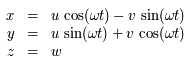 ,
,
et
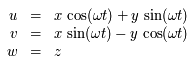 ,
,
-
Question 3
Solution :
Sous forme vectorielle on a 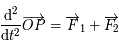 , soit :
, soit : 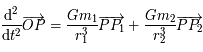 , où
, où 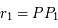 et
et 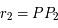 .
.
Sachant que les coordonnées de 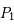 et
et 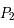 dans le repère fixe sont
dans le repère fixe sont 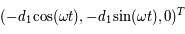 et
et 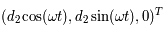 respectivement, on en déduit les équations du mouvement :
respectivement, on en déduit les équations du mouvement :
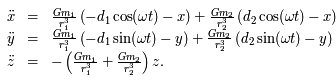
-
Question 4
Solution :
On a :
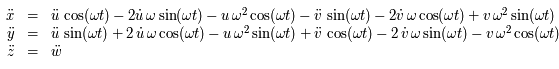 ,
,
En multipliant la première par 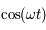 et la deuxième par
et la deuxième par 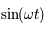 et en ajoutant d'une part, et en multipliant la première par
et en ajoutant d'une part, et en multipliant la première par
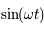 et la deuxième par
et la deuxième par 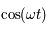 et en retranchant d'autre part, on obtient le système suivant :
et en retranchant d'autre part, on obtient le système suivant :
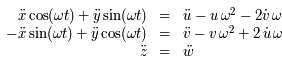 ,
,
Ainsi :
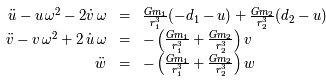 ,
,
-
Question 5
Solution :
On doit avoir :
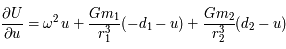 .
.
Or 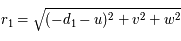 , ainsi
, ainsi 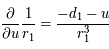 . De même
. De même 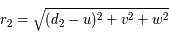 , ainsi
, ainsi 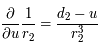 .
.
On en déduit que 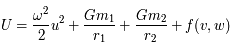 .
.
Finalement on a 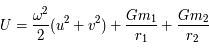 .
.
-
Question 6
Solution :
En effectuant l'opération demandée on obtient : 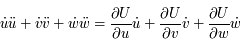 .
.
Ce qui est facilement intégrable et donne : 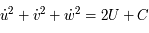 , où
, où 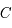 est une constante d'intégration.
est une constante d'intégration.
Ainsi 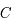 est une constante du mouvement.
est une constante du mouvement.
-
Question 7
Solution :
On a :
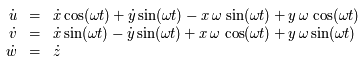
Ainsi 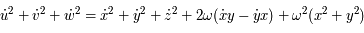 .
.
On en déduit 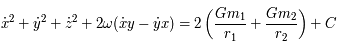
-
Question 8
Solution :
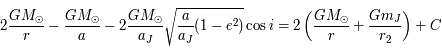 .
.
En négligeant 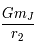 et avec
et avec 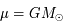 on obtient :
on obtient : 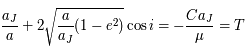 .
.
pages_int-mult/exo-photometrie.html
Exercice
'Soleil'
-
Question 1
Aide :
En première approximation, le Soleil rayonne comme un corps noir à la température de la photosphère (5780 K en moyenne).
Solution :
La luminance spectrale (ou chromatique) est donnée par la loi de Planck 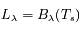
où 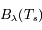 est la fonction de Plank pour la température de la photosphère. Il s'agit de la luminosité d'un élément de surface dans un intervalle de longueur d'onde et dans une direction donnée.
est la fonction de Plank pour la température de la photosphère. Il s'agit de la luminosité d'un élément de surface dans un intervalle de longueur d'onde et dans une direction donnée.
-
Question 2
Solution :
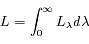
La loi de Stefan donne 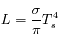 =
= 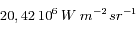
-
Question 3
Solution :
Chaque élément de surface rayonne en L cos e. En intégrant dans toutes les directions on trouve :
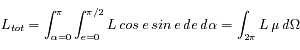
où 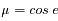 , et
, et 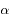 est l'azimuth. L'intégrale porte sur le demi-espace libre (
est l'azimuth. L'intégrale porte sur le demi-espace libre (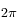 sr).
sr).
On a de façon évidente 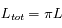 puisque la luminance L est isotrope par hypothèse.
puisque la luminance L est isotrope par hypothèse.
On remarque que la quantité L est intensive (non sommable). La quantité 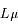 est la puissance diffusée par unité de surface, qui est sommable.
est la puissance diffusée par unité de surface, qui est sommable.
-
Question 4
Solution :
On intègre la quantité précédente sur toute la surface du Soleil :
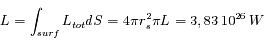
pages_int-mult/exo-photometrie.html
Exercice
'Surface lunaire'
pages_int-mult/exo-thm-liouville.html
Exercice
'théorème de Liouville'
-
Question 1
Solution :
D'après le théorème de Green-Astrograsdki, on a:
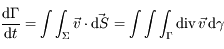 .
.
-
Question 2
Solution :
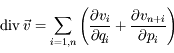 .
.
Or 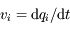 et
et 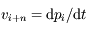 , donc en tenant compte des propriétés du flux hamiltonien données dans l'introduction on a:
, donc en tenant compte des propriétés du flux hamiltonien données dans l'introduction on a:
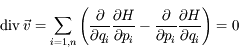 .
.
D'après la question précédente la conclusion est immédiate.
 Entropie
Entropie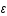 , aux variations d'entropie, S, et de volume, V, par la relation suivante:
, aux variations d'entropie, S, et de volume, V, par la relation suivante:
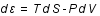 ,
où T est la température et P la pression.
,
où T est la température et P la pression.
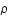 .
.
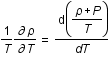 .
.
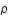 puis relier l'entropie à ces variables thermodynamiques.
puis relier l'entropie à ces variables thermodynamiques.
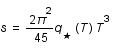 , où
, où 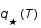 est un facteur dépendant de la température et des particules présentes. L'unité de volume est
est un facteur dépendant de la température et des particules présentes. L'unité de volume est 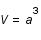 , où
, où 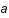 est le facteur d'échelle mesurant l'expansion de l'univers. Exprimer S comme une fonction de la température T et du facteur d'échelle a.
est le facteur d'échelle mesurant l'expansion de l'univers. Exprimer S comme une fonction de la température T et du facteur d'échelle a.
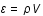
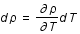
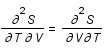 .
.
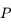 de masse unité mobile dans un plan et soumis à l'attraction gravitationnelle d'un corps fixe de masse
de masse unité mobile dans un plan et soumis à l'attraction gravitationnelle d'un corps fixe de masse 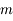 se trouvant en
se trouvant en 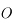 . On suppose que
. On suppose que 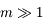 .
.
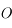 . On précise que la force universelle de la gravitation
s'appliquant au point
. On précise que la force universelle de la gravitation
s'appliquant au point 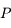 est:
est:
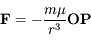 ,
,
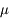 désigne la constante universelle de la gravitation et
désigne la constante universelle de la gravitation et 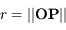 (les notations en gras dénotent des vecteurs).
(les notations en gras dénotent des vecteurs).
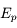 .
.
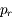 et
et 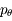 associées aux coordonnées
associées aux coordonnées 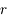 et
et 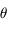 .
.
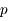 associée à la coordonnée
associée à la coordonnée 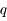 est définie par :
est définie par : 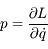 .
.
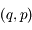 on a les équations:
on a les équations:
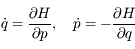 .
.
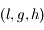 associées aux moments conjuguées
associées aux moments conjuguées 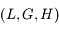 (voir ce
(voir ce 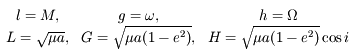 .
.
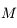 est
est 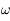 est
est 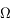 est
est 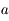 est
est 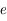 est
est  est
est 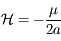 , (voir cet exercice sur l'
, (voir cet exercice sur l'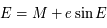 , ou d'écrire des développements utiles du problème des deux corps.
, ou d'écrire des développements utiles du problème des deux corps.
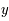 fonction de 2 variables
fonction de 2 variables 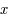 et
et 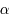 et d'une fonction
et d'une fonction 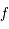 infiniment dérivable de la forme :
infiniment dérivable de la forme : 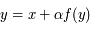 avec
avec 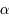 petit.
petit.
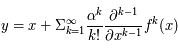 .
.
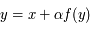 , alors
, alors 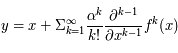 avec
avec 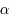 petit.
petit.
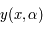 au voisinage de
au voisinage de 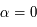 .
.
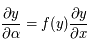 .
.
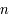 strictement positif,
strictement positif, 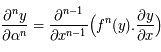 . On utilisera le résultat de la question précédente.
. On utilisera le résultat de la question précédente.
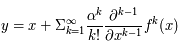 .
.
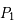 et
et 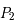 , appelés primaires et de masse respective
, appelés primaires et de masse respective 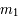 et
et 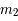 , sont sur des orbites circulaires et
, sont sur des orbites circulaires et 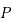 , de masse
négligeable voit sa trajectoire affectée
par les primaires alors que celui-ci n'affecte pas le mouvement des deux primaires. Ce problème est appelé le problème de trois corps restreint et circulaire.
, de masse
négligeable voit sa trajectoire affectée
par les primaires alors que celui-ci n'affecte pas le mouvement des deux primaires. Ce problème est appelé le problème de trois corps restreint et circulaire.
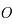 des deux primaires et dont les axes sont tels que l'axe des abscisses est dirigé vers le deuxième primaire, l'axe des ordonnées fait un angle de
des deux primaires et dont les axes sont tels que l'axe des abscisses est dirigé vers le deuxième primaire, l'axe des ordonnées fait un angle de 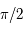 avec celui des abscisse dans le même sens que le mouvement de rotation des primaires, et l'axe des
avec celui des abscisse dans le même sens que le mouvement de rotation des primaires, et l'axe des 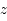 complète un trièdre direct.
complète un trièdre direct.
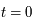 .
.
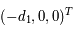 et
et 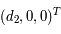 , où
, où 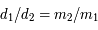 et
et 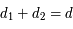 qui est la distance (fixe) qui sépare les deux primaires. On note
qui est la distance (fixe) qui sépare les deux primaires. On note 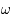 la vitesse de rotation angulaire des deux primaires par rapport au repère fixe.
la vitesse de rotation angulaire des deux primaires par rapport au repère fixe.
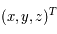 les coordonnées dans le repère fixe et
les coordonnées dans le repère fixe et 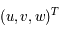 les coordonnées dans le repère tournant.
Le point au dessus d'une quantité indique la dérivée par rapport au temps de cette quantité.
les coordonnées dans le repère tournant.
Le point au dessus d'une quantité indique la dérivée par rapport au temps de cette quantité.
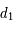 et
et 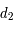 en fonction de
en fonction de 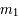 ,
, 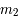 et
et 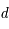 .
.
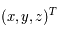 et
et 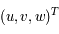 pour un même objet.
pour un même objet.
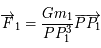 et
et 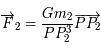 . En appliquant le principe fondamental de la dynamique, c'est-à-dire que l'accélération est égale à la somme des forces dans le repère fixe, écire les équations différentielles
vérifiées par les coordonnées
. En appliquant le principe fondamental de la dynamique, c'est-à-dire que l'accélération est égale à la somme des forces dans le repère fixe, écire les équations différentielles
vérifiées par les coordonnées 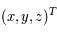 de
de 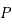 .
.
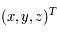 en fonction de
en fonction de 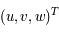 , en déduire les équations du mouvement dans le repère tournant.
, en déduire les équations du mouvement dans le repère tournant.
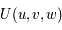 tel que le système d'équations précédent s'écrit :
tel que le système d'équations précédent s'écrit :
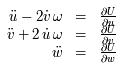 ,
,
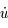 ,
, 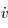 et
et 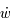 respectivement, puis en additionnant, montrer que le système admet une intégrale du mouvement (c'est -à-dire une quantité qui est constante au cours du temps).
respectivement, puis en additionnant, montrer que le système admet une intégrale du mouvement (c'est -à-dire une quantité qui est constante au cours du temps).
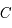 en fonction de
en fonction de 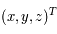 et de leur dérivées par rapport au temps.
et de leur dérivées par rapport au temps.
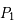 et
et 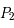 correspondent au Soleil et à Jupiter respectivement.
On pose
correspondent au Soleil et à Jupiter respectivement.
On pose 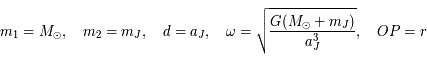 . Comme
. Comme 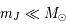 ,
on en déduit que
,
on en déduit que 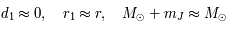 .
.
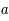 ,
, 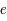 , et
, et 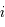 le demi-grand axe, l'excentricité et l'inclinaison de cette trajectoire. On a alors les relations suivantes:
le demi-grand axe, l'excentricité et l'inclinaison de cette trajectoire. On a alors les relations suivantes:
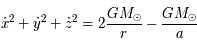 ,
, 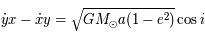 , réécrire l'équation précédente pour
, réécrire l'équation précédente pour 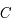 en fonction
de
en fonction
de 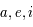 . L'expression obtenue correspond au paramètre de Tisserand qui est une quasi constante du mouvement pour les comètes
de la famille de Jupiter qui sont essentiellement soumisent à l'influence de Jupiter et du Soleil. On remarquera que les approximations faites
fonctionnent pourvu que l'on ne soit pas trop proche de Jupiter.
. L'expression obtenue correspond au paramètre de Tisserand qui est une quasi constante du mouvement pour les comètes
de la famille de Jupiter qui sont essentiellement soumisent à l'influence de Jupiter et du Soleil. On remarquera que les approximations faites
fonctionnent pourvu que l'on ne soit pas trop proche de Jupiter.

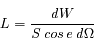
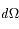 l'angle solide sous lequel la source voit le détecteur, et S la surface de la source. Dans le Système International, la luminance se mesure en
l'angle solide sous lequel la source voit le détecteur, et S la surface de la source. Dans le Système International, la luminance se mesure en 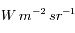 , ou dans un intervalle de longueur d'onde élémentaire en
, ou dans un intervalle de longueur d'onde élémentaire en 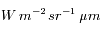 .
.
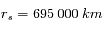 ).
).
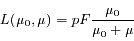
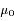 et
et 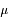 sont les cosinus des angles d'incidence et d'émergence.
sont les cosinus des angles d'incidence et d'émergence.

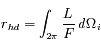
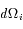 est l'angle solide élémentaire dans la direction d'incidence.
est l'angle solide élémentaire dans la direction d'incidence.
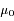 et
et 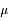 .
.

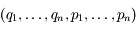 vérifie les équations différentielles suivantes :
vérifie les équations différentielles suivantes :
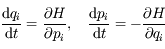 , avec
, avec 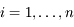 .
.
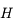 est le hamiltonien du système, indépendant du temps.
est le hamiltonien du système, indépendant du temps.
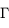 un volume de surface
un volume de surface 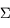 . La variation du volume au cours du temps s'écrit:
. La variation du volume au cours du temps s'écrit:
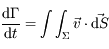 ,
,
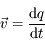 est le vecteur vitesse et
est le vecteur vitesse et 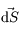 est un vecteur normal à la surface
est un vecteur normal à la surface 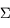 et de norme égale à une élément de surface.
et de norme égale à une élément de surface.
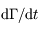 en vonction de la divergence de la vitesse
en vonction de la divergence de la vitesse 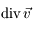 .
.
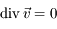 et donc que
et donc que 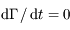 .
.
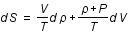
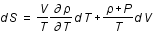
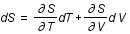
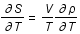 et
et 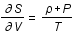 .
.
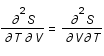 ,
, 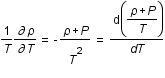
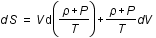 .
Donc,
.
Donc, 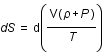 et
et 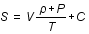 , où C est une constante d'intégration.
, où C est une constante d'intégration.
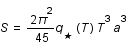
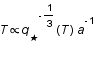 .
.
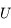 est tel que
est tel que 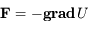 . Dans le repère polaire on a:
. Dans le repère polaire on a:
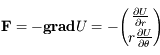 ,
,
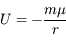 , en considérant que le potentiel est nul à l'infini.
L'énergie potentielle est donc:
, en considérant que le potentiel est nul à l'infini.
L'énergie potentielle est donc: 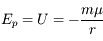 (on rappelle que la masse de
(on rappelle que la masse de 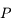 est égale à 1).
est égale à 1).
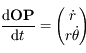 . Donc l'énergie cinétique est
. Donc l'énergie cinétique est 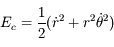 .
.
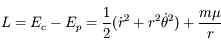 ,
,
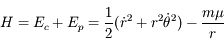 .
.
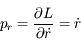 et
et 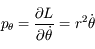
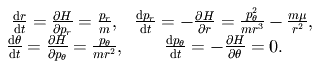
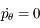 correspond à la loi des aires et découle du fait que
correspond à la loi des aires et découle du fait que 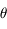 n'est pas présent explicitement dans le hamiltonien.
n'est pas présent explicitement dans le hamiltonien.
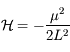 , ainsi les équations de hamilton nous donnent:
, ainsi les équations de hamilton nous donnent:
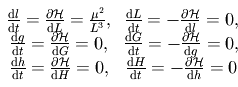 .
.
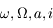 et
et 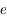 sont constants. Seule l'anomalie moyenne varie, et est donnée par
sont constants. Seule l'anomalie moyenne varie, et est donnée par 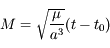 , où
, où 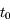 correspond au passage au péricentre, c'est à dire lorsque
correspond au passage au péricentre, c'est à dire lorsque 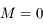 . Avec
. Avec 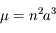 on retrouve bien la définition
on retrouve bien la définition 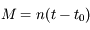 de l'anomalie moyenne donnée dans l'exercice sur l'
de l'anomalie moyenne donnée dans l'exercice sur l'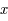 fixé et au voisinage de
fixé et au voisinage de 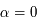 ,
, 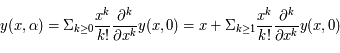
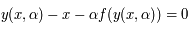 .
.
![\frac{\partial y}{\partial x} - 1 - \alpha \frac{\partial f}{\partial y} \frac{\partial y}{\partial x} = 0 \Longleftrightarrow \frac{\partial y}{\partial x} \Big{[} 1 - \alpha f'(y) \Big{]} = 1](../pages_der-part/equations_der-part/equation96.png) .
.
![\frac{\partial y}{\partial \alpha} - f(y(x,\alpha)) - \alpha \frac{\partial f}{\partial y} \frac{\partial y}{\partial \alpha} = 0 \Longleftrightarrow \frac{\partial y}{\partial \alpha} \Big{[} 1 - \alpha f'(y) \Big{]} = f(y)](../pages_der-part/equations_der-part/equation97.png) .
.
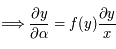 .
.
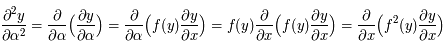 .
.
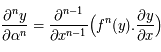 .
.
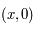 ,
, 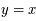 ,
, 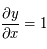 et
et 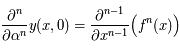 .
.
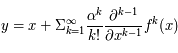 .
.
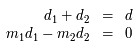 .
.
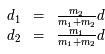 .
.
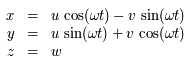 ,
,
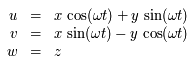 ,
,
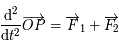 , soit :
, soit : 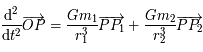 , où
, où 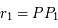 et
et 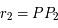 .
.
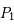 et
et 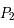 dans le repère fixe sont
dans le repère fixe sont 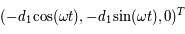 et
et 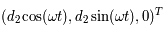 respectivement, on en déduit les équations du mouvement :
respectivement, on en déduit les équations du mouvement :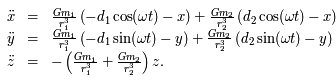
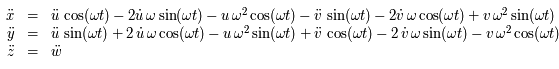 ,
,
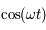 et la deuxième par
et la deuxième par 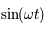 et en ajoutant d'une part, et en multipliant la première par
et en ajoutant d'une part, et en multipliant la première par
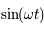 et la deuxième par
et la deuxième par 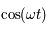 et en retranchant d'autre part, on obtient le système suivant :
et en retranchant d'autre part, on obtient le système suivant :
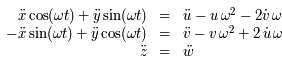 ,
,
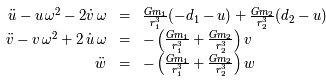 ,
,
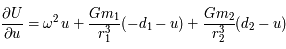 .
.
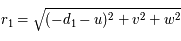 , ainsi
, ainsi 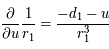 . De même
. De même 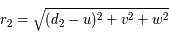 , ainsi
, ainsi 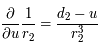 .
.
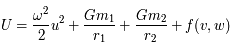 .
.
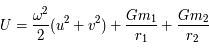 .
.
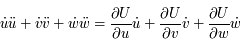 .
.
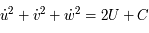 , où
, où 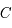 est une constante d'intégration.
est une constante d'intégration.
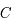 est une constante du mouvement.
est une constante du mouvement.
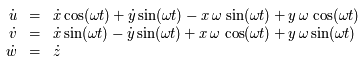
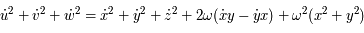 .
.
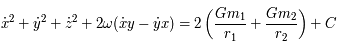
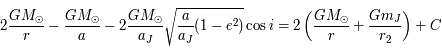 .
.
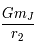 et avec
et avec 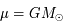 on obtient :
on obtient : 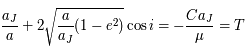 .
.
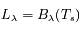
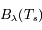 est la fonction de Plank pour la température de la photosphère. Il s'agit de la luminosité d'un élément de surface dans un intervalle de longueur d'onde et dans une direction donnée.
est la fonction de Plank pour la température de la photosphère. Il s'agit de la luminosité d'un élément de surface dans un intervalle de longueur d'onde et dans une direction donnée.
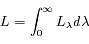
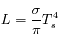 =
= 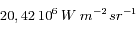
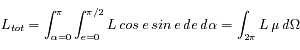
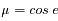 , et
, et 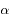 est l'azimuth. L'intégrale porte sur le demi-espace libre (
est l'azimuth. L'intégrale porte sur le demi-espace libre (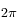 sr).
sr).
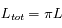 puisque la luminance L est isotrope par hypothèse.
puisque la luminance L est isotrope par hypothèse.
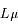 est la puissance diffusée par unité de surface, qui est sommable.
est la puissance diffusée par unité de surface, qui est sommable.
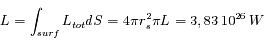
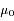 , le résultat est donc une fonction de
, le résultat est donc une fonction de 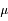 seul:
seul:
![r_{hd}(\mu) = 2p \left[ 1 - \mu Log \frac{\mu +1}{\mu} \right]](../pages_int-mult/equations_int-mult/equation27.png)
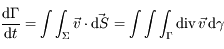 .
.
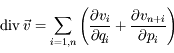 .
.
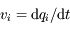 et
et 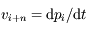 , donc en tenant compte des propriétés du flux hamiltonien données dans l'introduction on a:
, donc en tenant compte des propriétés du flux hamiltonien données dans l'introduction on a:
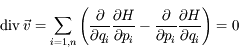 .
.