Ex : Excentricité limite dans les développements du problème à 2 corps

Auteurs: Alain Vienne, Stéphane Erard

Auteur: Alain Vienne

Excentricité limite dans les développements du problème à 2 corps

Difficulté : ☆☆☆ Temps : 1h30

Introduction

Dans le problème à 2 corps (voir, pour plus de détails, un cours d'astronomie, par exemple celui-ci) l'anomalie vraie et l'anomalie moyenne sont liées grâce à l'anomalie excentrique 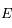par les 2 formules suivantes:

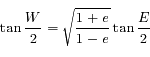$\tan \frac{W}{2} = \sqrt{\frac{1+e}{1-e}} \tan \frac{E}{2}$ , et

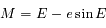$M=E-e\sin E$ qui est appelée "équation de Képler".

Question 1)

Sachant que est le petit paramètre, montrer que l'équation de Kepler est de la forme indiquée dans le théorème de Lagrange. Indiquer à quoi correspond chacun des paramètres de ce théorème dans notre problème.

Aide Solution

Question 2)

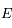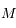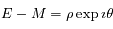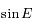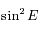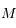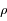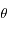
est donc complexe. On suppose réel et on pose: $E-M=\rho \exp \imath \theta$ (module et argument). Exprimer $\sin E$ puis $\sin ^2 E$ en fonction de , $\rho$ et $\theta$

Aide Aide Solution

Question 3)

Le contour 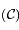$( \mathcal{C} )$ est défini par 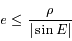$e \le \frac{\rho}{|\sin E|}$ . Le cas le plus défavorable correspond à 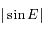$|\sin E |$ maximum. Donner les conditions sur 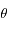$\theta$ et 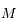correspondantes.

Aide Solution

Question 4)

Que devient 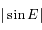$|\sin E |$ pour ces conditions?

Solution

Question 5)

Par la condition 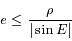$e \le \frac{\rho}{|\sin E|}$ , on cherche donc à maximiser 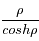$\frac{\rho}{cosh \rho}$ . Montrer que ce maximum est atteint pour 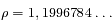$\rho = 1,1996784\dots$ En déduire la plus grande valeur de l'exentricité e_M .

Solution

Remarque

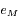Ainsi pour 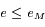$e \le e_M$ , on peut écrire:

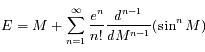$E=M+\sum_{n=1}^{\infty} \frac {e^n}{n!}\frac{d^{n-1}}{dM^{n-1}}(\sin ^n M )$ . Pour obtenir l'équation du centre, il faut encore utiliser la formule 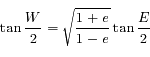$\tan \frac{W}{2} = \sqrt{\frac{1+e}{1-e}} \tan \frac{E}{2}$ pour revenir à 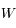. Mais cette formule ne pose aucun problème de convergence. La valeur de 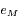e_M est donc inchangée.