

Ex: relations de Kramers-Kronig |
Difficulté : ☆☆ Temps : 60 min
Les équations de Maxwell dans un milieu matériel font intervenir un vecteur induction électrique défini comme :
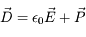
où 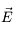 est le champ électrique appliqué,
est le champ électrique appliqué, 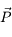 la polarisation électrique du milieu (qui décrit la réaction du milieu à l'application du champ électrique externe) et
la polarisation électrique du milieu (qui décrit la réaction du milieu à l'application du champ électrique externe) et 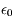 une constante physique appelée permittivité du vide.
une constante physique appelée permittivité du vide.
Les propriétés du milieu lui-même sont décrites par un certain type de relation entre le champ électrique et la polarisation. Dans un grand nombre de cas (milieu isotrope, champ faible...) cette relation peut s'écrire :
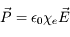
où 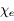 (la susceptibilité électrique) est a priori un tenseur d'ordre 2 dépendant du temps et de la position.
(la susceptibilité électrique) est a priori un tenseur d'ordre 2 dépendant du temps et de la position.
La solution des équations de Maxwell dans le milieu met en évidence l'indice de réfraction complexe de ce milieu :
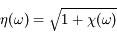
où 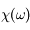 est la représentation en fréquence de
est la représentation en fréquence de 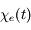 , c'est-à-dire sa transformée de Fourier.
, c'est-à-dire sa transformée de Fourier.
Déduire en utilisant le théorème de convolution une relation entre les représentations en fréquence du champ électrique et de la polarisation, puis entre G et 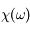 .
.
En supposant constantes les propriétés du milieu, comment peut-on simplifier la fonction G ?
On considère la fonction 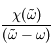 de la variable complexe
de la variable complexe 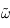 , où
, où 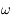 est réel. Montrer qu'elle est analytique dans la partie supérieure du plan complexe.
est réel. Montrer qu'elle est analytique dans la partie supérieure du plan complexe.
Trouver un contour d'intégration adéquat pour calculer l'intégrale de 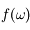 . Calculer l'intégrale. Commentaire ?
. Calculer l'intégrale. Commentaire ?
En déduire une relation entre parties réelle et imaginaire de 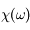 .
.
En explicitant les symétries de 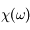 , trouver une autre écriture de ces relations.
, trouver une autre écriture de ces relations.