Ex: Spectre de puissance

Auteur: Jérôme Thiébaut

spectre de puissance

Difficulté : ☆☆☆ Temps : 25 min

Introduction

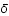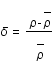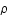On définit le contraste de densité delta par delta=(rho-accent(rho;barre))/accent(rho;barre) , où rho est la densité et 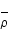la densité moyenne.

On travaille dans une boîte d'univers isotrope et plat de côté L (les mesures étant faites à partir d'observations, seul l'univers proche est accessible), on peut donc exprimer le champ de contraste de densité 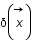delta(accent(x;->)) comme une série de Fourier:

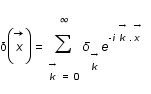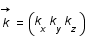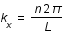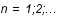delta(accent(x;->))=somme(delta_accent(k;->)*exp(-i*pscalaire(accent(k;->);accent(x;->)));accent(k;->)=0;infty) , où le vecteur accent(k;->) = matrice(ligne(k_x ; k_y; k_z)) est tel que k_x=n*2*pi/L avec n= 1;2;... .De même pour 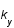k_y et k_z .

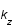On définit la fonction d'autocorrélation du champ de densité par :

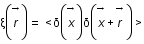xi(accent(r;->))=<delta(accent(x;->))*delta(accent(x;->)+accent(r;->))> , où la valeur moyenne s'effectue sur le volume de la boîte.

Question 1)

Exprimer la fonction d'autocorrélation en fonction de 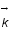accent(k;->) .

Solution

Question 2)

Ramener la double somme obtenue à une seule.

Aide Solution

Question 3)

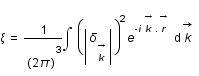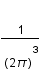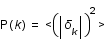Le passage de la somme en intégrale donne xi=(1/(2*pi)^3)*intégrale(abs(delta_accent(k;->))^2*exp(-i*pscalaire(accent(k;->);accent(r;->)));accent(k;->)) , où le facteur a été introduit par commodité. On définit le spectre de puissance comme : P(k)=<abs(delta_k)^2> .

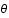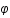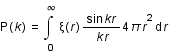Calculer la partie angulaire de l'intégrale (en coordonnées sphériques, intégrer selon theta et phi ) et exprimer le résultat en fonction du spectre de puissance. Si on inverse cette relation, on trouve que P(k)=intégrale(xi(r)*(sin(kr)/(k*r))*4*pi*r^2;r;0;infini) .

Les relevés de galaxies tel le SDSS, permettent, grâce à des modèles de profils de masse autour des galaxies, de remonter à une estimation du champ de densité. Après avoir calculé son autocorrélation, on peut donc calculer son spectre de puissance et le comparer à la théorie.

Aide Aide Solution