Courbe de vitesse nulle
Reprenons notre Hamiltonien. Si on réintroduit les vitesses relatives dans le référentiel en rotation
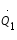
et
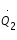
, on obtient :
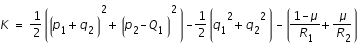
Puisque
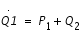
et
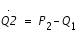
, et que la courbe de vitesse nulle s'écrit
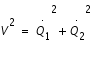
, nous obtenons :
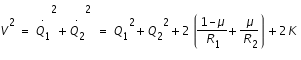
Or, nous avons
l'intégrale de Jacobi qui vaut J=-2K. L'équation de la courbe de vitesse nulle est donc la suivante :
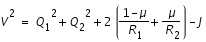
Pou une valeur fixé de J, le plan
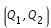
sera partagé en plusieurs régions. Celles où l'équation précédente est négative sont des zones où le mouvement n'est pas possible, ce sont des zones interdites. Les points
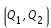
pour lesquels l'expression précédente s'annule forment les "courbes de vitesse nulle". Notons que c'est séparatrices ne sont pas interdites ! En effet, ce n'est pas parce que la vitesse s'y annule que l'accélération est elle même nulle. La trajectoire de la particule peut être tangente à ces courbes.
Bien entendu, c'est courbe ne sont visible que dans le repère non-tournant.
Pour une même valeur du paramètre de masse (ici
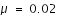
), il y a différents cas possibles :
- Pour une faible valeur de J, tout l'espace est accessible.
- Lorsque la valeur de l'intégrale de Jacobi (J) augmente, deux zones interdites symétrique se développent autour des points de Lagrange
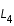 et
et 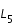 .
.
- Lorsqu'on augmente encore J, ces deux zones se rejoignent autour de
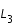 .
.
- Puis, ces deux zones se rejoignent aussi de l'autre côté, c'est-à-dire autour de
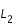 . Le plan
. Le plan 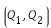 est alors séparé en deux régions qui ne peuvent communiquer entre elles. Si la sonde est lâchée au voisinage d'un des deux corps massif, elle ne peut s'échapper.
est alors séparé en deux régions qui ne peuvent communiquer entre elles. Si la sonde est lâchée au voisinage d'un des deux corps massif, elle ne peut s'échapper.
- Pour des valeurs toujours plus grandes de J, la zone interdit sépare le voisinage de
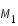 de celui de
de celui de 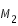 . La sonde est alors confiné au voisinage d'une seule des deux masses.
. La sonde est alors confiné au voisinage d'une seule des deux masses.

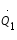 et
et 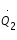 , on obtient :
, on obtient :
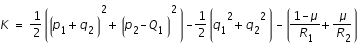
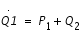 et
et 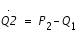 , et que la courbe de vitesse nulle s'écrit
, et que la courbe de vitesse nulle s'écrit 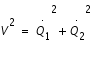 , nous obtenons :
, nous obtenons :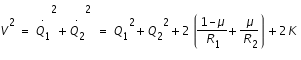
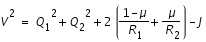
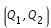 sera partagé en plusieurs régions. Celles où l'équation précédente est négative sont des zones où le mouvement n'est pas possible, ce sont des zones interdites. Les points
sera partagé en plusieurs régions. Celles où l'équation précédente est négative sont des zones où le mouvement n'est pas possible, ce sont des zones interdites. Les points 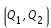 pour lesquels l'expression précédente s'annule forment les "courbes de vitesse nulle". Notons que c'est séparatrices ne sont pas interdites ! En effet, ce n'est pas parce que la vitesse s'y annule que l'accélération est elle même nulle. La trajectoire de la particule peut être tangente à ces courbes.
pour lesquels l'expression précédente s'annule forment les "courbes de vitesse nulle". Notons que c'est séparatrices ne sont pas interdites ! En effet, ce n'est pas parce que la vitesse s'y annule que l'accélération est elle même nulle. La trajectoire de la particule peut être tangente à ces courbes.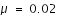 ), il y a différents cas possibles :
), il y a différents cas possibles :
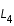 et
et 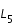 .
.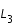 .
.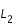 . Le plan
. Le plan 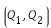 est alors séparé en deux régions qui ne peuvent communiquer entre elles. Si la sonde est lâchée au voisinage d'un des deux corps massif, elle ne peut s'échapper.
est alors séparé en deux régions qui ne peuvent communiquer entre elles. Si la sonde est lâchée au voisinage d'un des deux corps massif, elle ne peut s'échapper.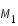 de celui de
de celui de 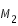 . La sonde est alors confiné au voisinage d'une seule des deux masses.
. La sonde est alors confiné au voisinage d'une seule des deux masses.