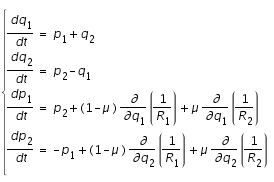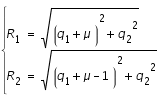Introduction de 'Integrateur Numerique'

Introduction

La trajectoire d'une particule dans un champ gravitationnel créé par deux masses peut être défini par les équations du mouvement de cette particule. A partir de ces équations (si on les résoud), il est possible de décrire la trajectoire de cette particule.

Equations du mouvement

Les équations du mouvement de notre particule sont les suivantes :
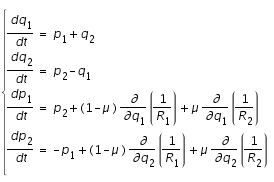
système(dq_1/dt = p_1 + q_2 ; dq_2/dt = p_2 - q_1 ; dp_1/dt = p_2 +(1-mu) * ( part/partq_1)(1/R_1) + mu * ( part/partq_1)(1/R_2) ; dp_2/dt = -p_1 +(1-mu) * ( part/partq_2)(1/R_1) + mu * ( part/partq_2)(1/R_2))

système(dq_1/dt = p_1 + q_2 ; dq_2/dt = p_2 - q_1 ; dp_1/dt = p_2 +(1-mu) * ( part/partq_1)(1/R_1) + mu * ( part/partq_1)(1/R_2) ; dp_2/dt = -p_1 +(1-mu) * ( part/partq_2)(1/R_1) + mu * ( part/partq_2)(1/R_2))

où

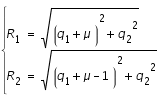
système(R_1 = sqrt( (q_1 + mu )^2 +q_2^2 ); R_2 = sqrt( (q_1 + mu - 1)^2 +q_2^2 ))

Le problème est que nous ne savons pas résoudre ce système analytiquement. Il nous est donc impossible de trouver une expression analytique pour la trajectoire. C'est pourquoi nous allons utiliser un intégrateur numérique.