Principe de la méthode de Runge-Kutta
L'idée de cette ensemble de méthodes est d'essayer de répartir les endroits où l'on évalue
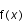
entre les abscisses
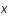
et
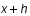
, plutôt que de calculer les dérivées successives jusqu'à un certain ordre de
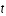
en un point.
Soient
On définit la méthode (implicite) de Runge-Kutta à E-étages par
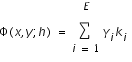
(2)
où
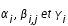
seront déterminés de façon à définir la méthode d'ordre le plus élevé possible.
Notons qu'il existe deux grandes familles de formules d'intégration numérique : les formules explicites et les formules implicites. Les secondes sont généralement stables alors que les premières ne le sont pas toujours.

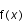 entre les abscisses
entre les abscisses 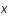 et
et 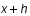 , plutôt que de calculer les dérivées successives jusqu'à un certain ordre de
, plutôt que de calculer les dérivées successives jusqu'à un certain ordre de 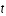 en un point.
en un point.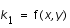
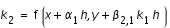
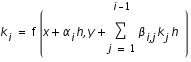
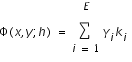 (2)
(2)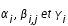 seront déterminés de façon à définir la méthode d'ordre le plus élevé possible.
seront déterminés de façon à définir la méthode d'ordre le plus élevé possible.