Principe de la méthode de Runge-Kutta (RK2)
Les méthodes à deux étages (E=2)
En partant de l'équation
(2), on trouve
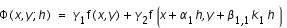
,
en utilisant le développement de Taylor sur le second terme, on obtient
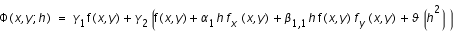
finalement en regroupant les termes, on a
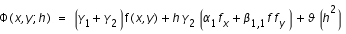
Pour que la méthode soit d'ordre 2, on fait l'analogie avec l'équation
(1) et on trouve que :
on obtient le système suivant
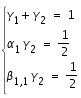
(3)
Ce système à deux caractéristiques importantes propres à toutes les méthodes de Runge-Kutta :
- ce sont des équations non linéaires,
- le système est sous-déterminés (plus d'inconnues que d'équations) et admet donc une infinité de solutions.
Retournons à présent au système
(3), il s'agit de résoudre 3 équations à 4 inconnues, il y a donc une infinité simple (4-3=1) de solutions.
On en conclut qu'il y a une infinité de formules de Runge-Kutta à 2 étages et elles sont toutes d'ordre 2.
-
Exemple
-
-
Méthode de Heun
-
Si on regarde notre système (3), cette méthode correspond au cas où
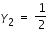 et donc,
et donc, 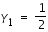 ,
, 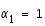 et
et 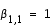 . Cette méthode se formule comme suit :
. Cette méthode se formule comme suit :
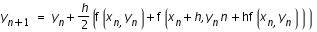
Point de vue géométrique
-
Méthode de la tangente améliorée
-
A nouveau, en regard avec notre système (3), cette méthode correspond au cas où
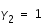 et donc,
et donc, 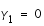 ,
, 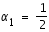 et
et 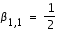 . Cette méthode se formule de la façon suivante :
. Cette méthode se formule de la façon suivante :


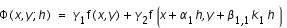 ,
,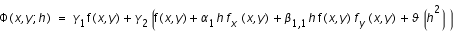
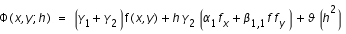
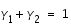
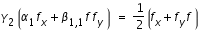
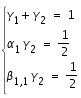 (3)
(3)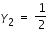 et donc,
et donc, 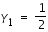 ,
, 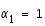 et
et 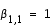 . Cette méthode se formule comme suit :
. Cette méthode se formule comme suit : 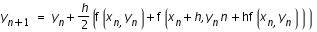
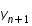 en
en 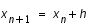 connaissant
connaissant 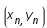 et
et 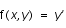 .
.
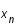 , c'est-à-dire la tangente. On la prolonge pour avoir la valeur en
, c'est-à-dire la tangente. On la prolonge pour avoir la valeur en 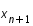 . Ceci correspond à la méthode d'Euler.
. Ceci correspond à la méthode d'Euler.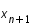 . On prend la parallèle de cette pente passant par
. On prend la parallèle de cette pente passant par 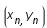 . On la prolonge pour obtenir la valeur en
. On la prolonge pour obtenir la valeur en 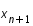 .
.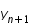 comme l'image de
comme l'image de 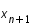 sur la droite obtenue.
sur la droite obtenue.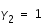 et donc,
et donc, 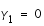 ,
, 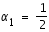 et
et 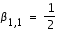 . Cette méthode se formule de la façon suivante :
. Cette méthode se formule de la façon suivante : 