Rappels de cours
On s'intéresse aux méthodes à un pas, définies par la relation de récurrence
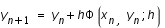
pour une certaine fonction
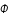
.
-
Définition
-
La méthode définie par la récurrence est dite d'ordre p si pour toute équation différentielle
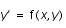 avec la condition initiale
avec la condition initiale 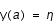 intégrable, dont la solution est
intégrable, dont la solution est 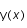

![C^1*[a,b]](../../../../images/trois-corps-integration/equations_integrateur_numerique/equation23.png) , on a
, on a 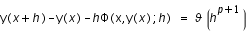
Pour augmenter l'ordre, on peut utiliser la méthode de Taylor : dans l'équation
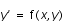
, on considère que
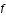
est différentiable jusqu'à l'ordre p. On peut alors écrire
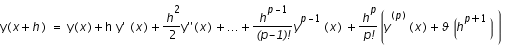
Lorsque l'on prend
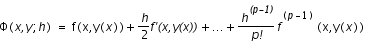
(1)
où
-
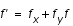
-
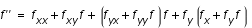
- ...
On obtient une méthode d'ordre p.
Le gros inconvénient de cette méthode, c'est qu'elle exige de calculer des dérivées successives de
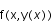
à chaque itération.

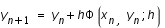 pour une certaine fonction
pour une certaine fonction 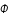 .
.
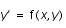 avec la condition initiale
avec la condition initiale 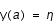 intégrable, dont la solution est
intégrable, dont la solution est 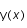

![C^1*[a,b]](../../../../images/trois-corps-integration/equations_integrateur_numerique/equation23.png) , on a
, on a 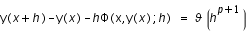
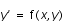 , on considère que
, on considère que 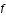 est différentiable jusqu'à l'ordre p. On peut alors écrire
est différentiable jusqu'à l'ordre p. On peut alors écrire
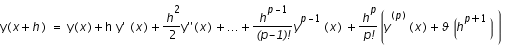
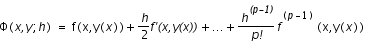 (1)
(1)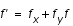
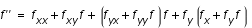
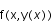 à chaque itération.
à chaque itération.