Méthode à pas variable (Runge-Kutta 4)
Méthode à pas variable (Runge-Kutta 4)
La figure suivante nous montre l'intérêt du pas variable.

Idée : faire les calculs deux fois :
- on calcul une première fois
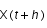 (noté
(noté 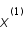 ) à partir de
) à partir de 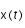 par une méthode de Runge-Kutta 4 (RK4).
par une méthode de Runge-Kutta 4 (RK4).
- on recommence avec un pas
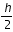 en faisant deux fois le calcul : on calcul
en faisant deux fois le calcul : on calcul  par RK4 à partir de
par RK4 à partir de 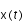 ; puis, par RK4 on calcule
; puis, par RK4 on calcule 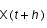 (noté
(noté 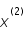 ) à partir de
) à partir de 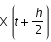
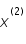
sera donc plus précis.
-
Si le pas
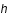 est trop grand, c'est à dire que
est trop grand, c'est à dire que 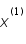 est fort différent de
est fort différent de 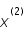 :
: 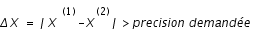
Alors, on diminue le pas et on recommence cette étape.
-
Si le pas
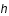 est adapté, c'est à dire
est adapté, c'est à dire 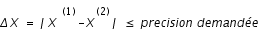
Alors, on passe à l'étape suivante et la prochaine fois, le pas sera augmenté.
C'est de cette façon que se fait l'adaptation du pas.
Nous allons maintenant donner et démontrer l'équation pour l'adaptation du pas :
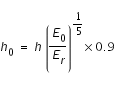
où
-
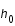 est le nouveau pas,
est le nouveau pas,
-
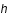 est le pas précédemment calculé,
est le pas précédemment calculé,
-
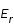 est l'erreur en objectif,
est l'erreur en objectif,
-
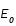 est l'erreur réalisée.
est l'erreur réalisée.
-
Démonstration
-
Écrivons l'équation de RK4 :
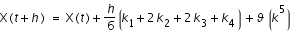
que nous écrivons : 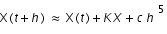
où 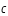 ne varie pas beaucoup.
ne varie pas beaucoup.
L'erreur réalisée est 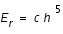 et l'erreur objectif est
et l'erreur objectif est 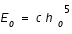 .
.
En combinant les deux équations précédentes, nous obtenons : 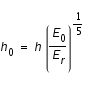 .
.
Pour se garder une marge d'erreur, nous multiplions ce résultat par 0.9.

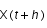 (noté
(noté 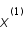 ) à partir de
) à partir de 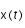 par une méthode de Runge-Kutta 4 (RK4).
par une méthode de Runge-Kutta 4 (RK4).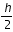 en faisant deux fois le calcul : on calcul
en faisant deux fois le calcul : on calcul  par RK4 à partir de
par RK4 à partir de 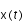 ; puis, par RK4 on calcule
; puis, par RK4 on calcule 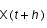 (noté
(noté 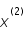 ) à partir de
) à partir de 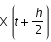
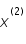 sera donc plus précis.
sera donc plus précis.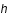 est trop grand, c'est à dire que
est trop grand, c'est à dire que 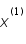 est fort différent de
est fort différent de 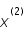 :
: 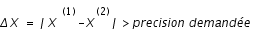
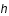 est adapté, c'est à dire
est adapté, c'est à dire 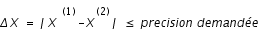
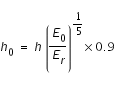
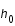 est le nouveau pas,
est le nouveau pas,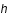 est le pas précédemment calculé,
est le pas précédemment calculé,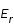 est l'erreur en objectif,
est l'erreur en objectif,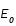 est l'erreur réalisée.
est l'erreur réalisée.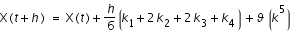
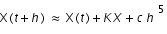
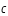 ne varie pas beaucoup.
ne varie pas beaucoup.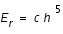 et l'erreur objectif est
et l'erreur objectif est 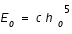 .
.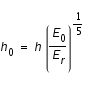 .
.