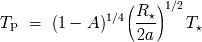Ejercicio 'Equilibrio térmico de un planeta'
Ejercicio 'Equilibrio térmico de un planeta'
Nivel **
Tiempo necesario :
60 min
En este ejercicio, nos vamos a interesar en el balance radiativo de un planeta en una órbita
circular de radio

alrededor de su estrella. Se supone el espacio interplanetario vacío. Ello implica la conservación
del flujo estelar integrado sobre toda superficie que rodee la estrella. La rotación propia del
planeta es suficientemente rápida para que se pueda considerar su temperatura
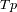
como uniforme sobre toda la superficie. Se menosprecia otra fuente de energía que la
proveniente de la estrella.
El planeta refleja una fracción
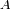
de la radiación solar, y absorbe una fracción
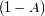
, donde
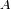
es el albedo. En una primera aproximación, a baja resolución espectral, se considera que el espectro del
planeta se constituye por la superposición de dos espectros de cuerpo negro de los cuales queremos
determinar las temperaturas. Se define
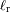
como la componente absorbida y radiada.
1)
Demostrar que la potencia interceptada por el planeta vale:
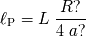
donde
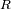
representa el radio del planeta.
ayuda
solución
2)
Calcular la razón
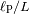
de Júpiter y de la Tierra
| Objeto |
 (UA)
(UA) |
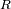 (km)
(km) |
| Júpiter |
5.2 |
71000 |
| Tierra |
1 |
6400 |
Recuerda que
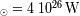
.
ayuda
solución
3)
El planeta está en equilibrio termodinámico. Expresar
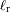
y
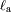
en función de la luminosidad total
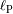
y del albedo
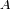
.
ayuda
solución
4)
¿Cuál es la temperatura
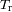
asociada a la radiación reflejada
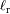
, asimilada a la radiación de un cuerpo negro?
ayuda
solución
5)
Demostrar que la temperatura asociada a la componente
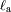
, se aproxima a la temperatura de equilibrio del planeta y que por lo tanto :
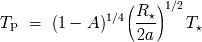 ayuda
solución
ayuda
solución
6)
Hacer la aplicación numérica para un exoplaneta con un
albedo de

y un semieje mayor de
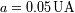
. La estrella tiene las propiedades siguientes :
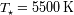
y
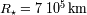
.
ayuda
solución
7)
Deducir la longitud de onda
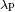
que corresponde al máximo de la emisión planetaria. ¿Cuál es el dominio espectral
correspondiente?
ayuda
solución

 alrededor de su estrella. Se supone el espacio interplanetario vacío. Ello implica la conservación
del flujo estelar integrado sobre toda superficie que rodee la estrella. La rotación propia del
planeta es suficientemente rápida para que se pueda considerar su temperatura
alrededor de su estrella. Se supone el espacio interplanetario vacío. Ello implica la conservación
del flujo estelar integrado sobre toda superficie que rodee la estrella. La rotación propia del
planeta es suficientemente rápida para que se pueda considerar su temperatura
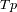 como uniforme sobre toda la superficie. Se menosprecia otra fuente de energía que la
proveniente de la estrella.
El planeta refleja una fracción
como uniforme sobre toda la superficie. Se menosprecia otra fuente de energía que la
proveniente de la estrella.
El planeta refleja una fracción
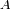 de la radiación solar, y absorbe una fracción
de la radiación solar, y absorbe una fracción
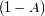 , donde
, donde
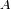 es el albedo. En una primera aproximación, a baja resolución espectral, se considera que el espectro del
planeta se constituye por la superposición de dos espectros de cuerpo negro de los cuales queremos
determinar las temperaturas. Se define
es el albedo. En una primera aproximación, a baja resolución espectral, se considera que el espectro del
planeta se constituye por la superposición de dos espectros de cuerpo negro de los cuales queremos
determinar las temperaturas. Se define
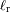 como la componente absorbida y radiada.
como la componente absorbida y radiada.
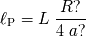
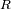 representa el radio del planeta.
ayuda
solución
representa el radio del planeta.
ayuda
solución
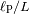 de Júpiter y de la Tierra
de Júpiter y de la Tierra
 (UA)
(UA)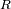 (km)
(km)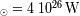 .
ayuda
solución
.
ayuda
solución
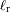 y
y
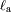 en función de la luminosidad total
en función de la luminosidad total
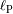 y del albedo
y del albedo
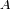 .
ayuda
solución
.
ayuda
solución
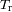 asociada a la radiación reflejada
asociada a la radiación reflejada
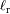 , asimilada a la radiación de un cuerpo negro?
ayuda
solución
, asimilada a la radiación de un cuerpo negro?
ayuda
solución
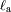 , se aproxima a la temperatura de equilibrio del planeta y que por lo tanto :
, se aproxima a la temperatura de equilibrio del planeta y que por lo tanto :