La métrica de Robertson-Walker
En un modelo del universo no-estático con espacio tiempo variable, la ley de Hubble existe,
incluso si todas las galaxias son comóviles con el sistema de coordenadas, es decir, si su energía
cinética es nula, sin contar los movimientos propios.
La métrica no-estática más general es la métrica de Robertson-Walker que se escribe:
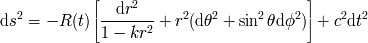
donde

,

,
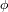
son los patámetros del espacio y

el tiempo. La función
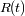
representa el radio del universo a un instante

.
-
si
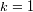 , el universo es de geometría esférica, y el espacio es finito.
, el universo es de geometría esférica, y el espacio es finito.
-
si
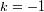 , el universo es de geometría hiperbólica, y el espacio es a cada instante abierto e infinito.
, el universo es de geometría hiperbólica, y el espacio es a cada instante abierto e infinito.
-
su
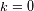 , el universo es de geometría parabólica, y el espacio es también abierto e infinito, pero a
cada instante es isométrico a un espacio plano euclídeo.
, el universo es de geometría parabólica, y el espacio es también abierto e infinito, pero a
cada instante es isométrico a un espacio plano euclídeo.
Los modelos de Friedmann
El principio cosmológico y la edad del universo
Si suponemos que el universo es homogéneo e isótropo (principio cosmológico), el modelo está
completamente definido por tres parámetros : el valor de la constante cosmológica
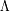
, el valor actual de la constante de Hubble
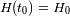
, y el valor actual del parámetro de densidad
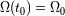
(o del parámetro de desaceleración actual
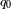
). Consideramos generalmente que la presión

del fluído de galaxia es nulo, lo que implica según las ecuaciones (1.1) y (1.2) que
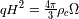
, y entonces que
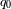
et
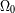
son intercambiables.
En los modelos de Friedman caracterizados por una constante cosmológica nula (
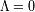
), la expansión se frena a lo largo del tiempo ; resulta que la edad
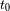
del Universo es siempre inferior al tiempo de Hubble
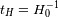
.

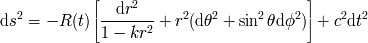
 ,
,
 ,
,
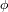 son los patámetros del espacio y
son los patámetros del espacio y
 el tiempo. La función
el tiempo. La función
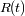 representa el radio del universo a un instante
representa el radio del universo a un instante
 .
.
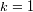 , el universo es de geometría esférica, y el espacio es finito.
, el universo es de geometría esférica, y el espacio es finito.
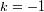 , el universo es de geometría hiperbólica, y el espacio es a cada instante abierto e infinito.
, el universo es de geometría hiperbólica, y el espacio es a cada instante abierto e infinito.
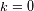 , el universo es de geometría parabólica, y el espacio es también abierto e infinito, pero a
cada instante es isométrico a un espacio plano euclídeo.
, el universo es de geometría parabólica, y el espacio es también abierto e infinito, pero a
cada instante es isométrico a un espacio plano euclídeo.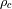 (universo parabólico) no conduce a un modelo hiperbólico infinito.
La determinación de la función de métrica
(universo parabólico) no conduce a un modelo hiperbólico infinito.
La determinación de la función de métrica
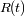 permite de describir la evolución del universo en el curso del tiempo. Aplicar las ecuaciones
de Einstein a la métrica de Robertson-Walker nos conduce a las dos ecuaciones diferenciales
siguientes :
permite de describir la evolución del universo en el curso del tiempo. Aplicar las ecuaciones
de Einstein a la métrica de Robertson-Walker nos conduce a las dos ecuaciones diferenciales
siguientes :
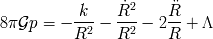
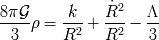
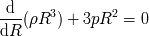
 es la presión del fluído de galaxias,
es la presión del fluído de galaxias,
 la densidad de la materia , y
la densidad de la materia , y
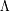 la constante cosmológica .
la constante cosmológica .
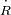 y
y
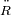 son las derivadas primera y segunda respectivamente del radio del universo
son las derivadas primera y segunda respectivamente del radio del universo
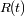 con respecto al tiempo.
Definimos:
con respecto al tiempo.
Definimos:
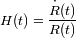 la constante de Hubble a un instante
la constante de Hubble a un instante
 , es decir, la tasa de expansión a un instante
, es decir, la tasa de expansión a un instante
 .
.
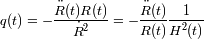 , el parámetro de desaceleración.
, el parámetro de desaceleración.
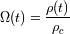 , el parámetro de densidad.
, el parámetro de densidad.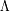 , el valor actual de la constante de Hubble
, el valor actual de la constante de Hubble
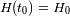 , y el valor actual del parámetro de densidad
, y el valor actual del parámetro de densidad
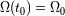 (o del parámetro de desaceleración actual
(o del parámetro de desaceleración actual
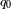 ). Consideramos generalmente que la presión
). Consideramos generalmente que la presión
 del fluído de galaxia es nulo, lo que implica según las ecuaciones (1.1) y (1.2) que
del fluído de galaxia es nulo, lo que implica según las ecuaciones (1.1) y (1.2) que
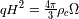 , y entonces que
, y entonces que
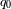 et
et
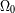 son intercambiables.
son intercambiables.
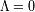 ), la expansión se frena a lo largo del tiempo ; resulta que la edad
), la expansión se frena a lo largo del tiempo ; resulta que la edad
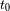 del Universo es siempre inferior al tiempo de Hubble
del Universo es siempre inferior al tiempo de Hubble
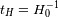 .
.