
|
Notions élémentaires de statistiques
La définition d'un bruit repose sur ses propriétés statistiques. Cette page rappelle des notions simples de statistiques, en distinguant les lois de probabilité, leurs réalisations, et l'estimation de paramètres statistiques.
La loi de probabilité d'une variable aléatoire 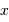 va être donnée par
va être donnée par 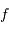 sa densité de probabilité, ou bien
sa densité de probabilité, ou bien 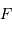 sa fonction de répartition
sa fonction de répartition 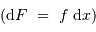 .
.
Parmi les moments centrés associés,
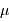 la moyenne et
la moyenne et 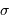 l'écart-type sont respectivement définis par :
l'écart-type sont respectivement définis par :
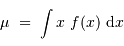
et :
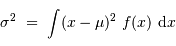
(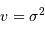 est la variance).
est la variance).
Une loi statistique possède des propriétés particulières, qui caractérisent tel ou tel phénomène : une loi poissonnienne (discrète) rend compte de l'arrivée d'événements indépendants, une loi gaussienne est souvent issue de l'addition d'un grand nombre de phénomènes indépendants...
La réalisation d'une loi de probabilité est aléatoire : un tirage de dés, réalisé 6 fois, ne conduira pas nécessaire à l'obtention une fois et une seule de chaque chiffre de 1 à 6. Plus le nombre de réalisations est grand, meilleur est l'accord entre l'observation de ces réalisations et la loi de probabilité.
En pratique, il faut distinguer d'une part la valeur moyenne 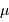 de la densité de probabilité de sa mesure
de la densité de probabilité de sa mesure 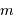 . Avec
. Avec 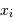 les réalisations d'une variable aléatoire, on a accès seulement à :
les réalisations d'une variable aléatoire, on a accès seulement à :
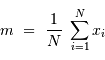
Et il n'y a aucune raison que 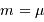 . En fait, c'est de mieux en mieux réalisé lorsque
. En fait, c'est de mieux en mieux réalisé lorsque 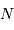 devient très grand.
devient très grand.
La variance 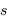 est mesurable par :
est mesurable par :
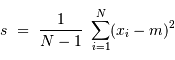
avec 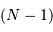 au dénominateur car
au dénominateur car 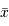 a déjà été obtenu à l'aide des
a déjà été obtenu à l'aide des 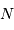 mesures, et il ne reste plus que
mesures, et il ne reste plus que 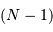 valeurs indépendantes pour estimer
valeurs indépendantes pour estimer 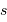 .
.
L'écart entre 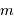 et
et 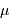 vaut typiquement
vaut typiquement 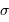 .
.