
 Hypertélescope
Hypertélescope
Difficulté : ☆☆☆
Temps : 60 min
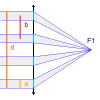
La première figure donne le schéma
de principe d'un hypertélescope. L'équivalent du miroir primaire
est constitué de sous-pupilles, reconstituant de façon incomplète
une surface collectrice correspondant à une immense parabole.
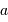 mesure le diamètre d'une sous-pupille ;
mesure le diamètre d'une sous-pupille ; 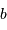 leur écartement.
leur écartement.
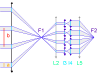
La deuxième figure présente le montage du densificateur de pupille. Les lentilles L2 et L5 sont supposées identiques, si bien que le grossissement du système constitué de ces lentilles vaut -1 ; le grossissement angulaire du système afocal constitué des lentilles l3 et l4 est noté 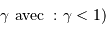 .
.
Cet exercice est à résoudre sans gros calcul ! Pour simplifier l'approche, on travaille sur une seule dimension, comme le montre la figure (sans chercher à reconstituer la surface collectrice).
Question 1)
On s'intéresse juste à l'optique en amont de F1. Quels paramètres
dimensionnent la taille angulaire de la tache image en F1 d'une
sous-pupille, de l'ensemble des sous-pupilles ? Mener l'analogie avec un réseau d'interférence composé de fentes de largeur 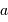 séparées d'une distance
séparées d'une distance 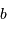 , s'étalant sur une longueur totale
, s'étalant sur une longueur totale 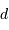 .
.
AideAideSolution
Réfléchir au rôle de la diffraction par une sous-pupille,
à celui des interférences entres sous-pupilles.
Mener l'analogie avec un réseau.
L'analogie avec un réseau de diffraction est immédiate. Une
sous-pupille se comportant comme une fente individuelle d'un
réseau de diffraction. Chaque sous-pupille diffracte le faisceau
pour une tache image individuelle 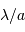 ; les
interférences entre les sous-faisceaux conduisent à une taille
angulaire
; les
interférences entre les sous-faisceaux conduisent à une taille
angulaire 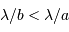 .
.
Question 2)
Déterminer l'action du système (l3, l4), en comparant les
situations en F1 et F2.
AideSolution
Pour une comparaison aisée, imaginer que L2 et L5 ont les mêmes diamètre et focale que L1.
Question 3)
Quel est l'intérêt du système ? Que se passe-t-il lorsque 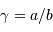 ?
?
AideAideSolution
Mener un raisonnement géométrique s'appuyant sur la figure.
S'intéresser à la localisation de l'énergie dans les pics d'interférence.
Lorsque 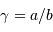 , tout se passe comme si l'on avait réuni des collecteurs de diamètre plus important et qu'il n'y avait plus de trous dans le miroir équivalent. La pupille a été densifiée.
, tout se passe comme si l'on avait réuni des collecteurs de diamètre plus important et qu'il n'y avait plus de trous dans le miroir équivalent. La pupille a été densifiée.
Question 4)
Qu'a-t-on gagné, qu'a-t-on perdu avec cette opération ?
AideAideAideSolution
S'intéresser à la tache de diffraction.
S'intéresser au champ accessible, dimensionné par une tache de diffraction élémentaire
Que devient la tache de diffraction d'une sous-pupille ?
Le gain en termes de formation d'image est clair : on a reconstitué un plus grand miroir, et donc les images sont plus piquées (la fonction d'étalement du point est moins... étalée). Mais, comme la tache de diffraction d'une
sous-pupille a été divisée par 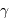 . Il en est de même du champ : le champ accessible par l'instrument a été réduit. Il y a toujours des compromis à faire.
. Il en est de même du champ : le champ accessible par l'instrument a été réduit. Il y a toujours des compromis à faire.

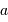 mesure le diamètre d'une sous-pupille ;
mesure le diamètre d'une sous-pupille ; 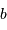 leur écartement.
leur écartement.
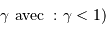 .
.
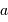 séparées d'une distance
séparées d'une distance 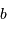 , s'étalant sur une longueur totale
, s'étalant sur une longueur totale 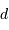 .
.