
|
Difficulté : ☆☆ Temps : 30 min
Au milieu du XVIIIe siècle, les missions de La Condamine au Pérou et de Maupertuis au Laponie ont conduit à la mesure de la longueur d'un degré du méridien en Laponie (aux alentours de la latitude 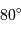 ) ainsi qu'au Pérou (vers
) ainsi qu'au Pérou (vers 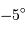 ). Il s'agissait de lever une controverse concernant la "figure" de la Terre, c'est à dire sa forme : aplatie aux pôles, ou bien en forme de ballon de rugby ?
). Il s'agissait de lever une controverse concernant la "figure" de la Terre, c'est à dire sa forme : aplatie aux pôles, ou bien en forme de ballon de rugby ?
Expliquer pourquoi la longueur d'un degré le long du méridien diffère entre ces 2 régions. Faire un schéma.
La Terre étant aplatie aux pôles, le rayon de courbure local est-il plus important au pôle ou à l'équateur ? Quel degré de méridien correspond à la plus grande longueur ?
La longueur 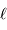 d'un arc de méridien d'ouverture
d'un arc de méridien d'ouverture 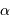 s'écrit en fonction du rayon de courbure
s'écrit en fonction du rayon de courbure 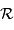 :
:
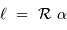
En représentation paramétrique, on repère un point de l'ellipse de révolution par
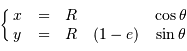
avec 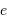 le paramètre marquant l'aplatissement.
Le rayon de courbure s'écrit, au 1er ordre en
le paramètre marquant l'aplatissement.
Le rayon de courbure s'écrit, au 1er ordre en 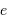 :
:
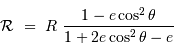
[on peut retrouver ce résultat en appliquant la définition : 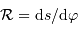 , avec
, avec 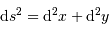 et
et 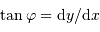 ].
].
Les mesures pour tourner de 1 degré donnant respectivement 57395 toises en Laponie, et 56735 toises au Pérou (57097 au sud de Paris), en déduire un ordre de grandeur de l'aplatissement de la Terre, exprimé comme la différence relative entre les rayons au pôle et à l'équateur.