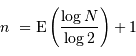
Signal analogique et numérisé sur 8 bits (64 valeurs possibles). La différence entre les valeurs réelles et codées introduit un
bruit de numérisation.
Crédit :
ASM
Bruit de numérisation
Le simple fait de numériser un signal analogique, càd de le coder sur une échelle de valeurs discrétisée (typiquement, sur 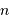 bits, ce qui permet de coder
bits, ce qui permet de coder 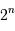 valeurs), peut rajouter du bruit au signal.
valeurs), peut rajouter du bruit au signal.
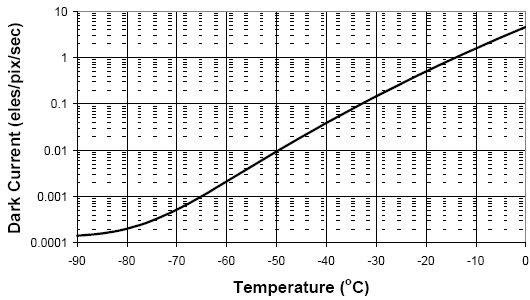
Le signal d'obscurité est un bruit d'origine thermique. Données pour une caméra CCD, en fontions de la température. A -15 deg, 1 électron thermique est généré par pixel par seconde ; à -65 deg, il faut attendre 1000 s pour qu'un moyenne un électron thermique apparaisse par pixel.
Crédit :
ANDOR
Bruit d'origine thermique
La température du détecteur conditionne le signal d'obscurité d'un détecteur. Suite à l'agitation thermique, des porteurs de charge apparaissent aléatoirement, d'autant plus que la température est élevée.
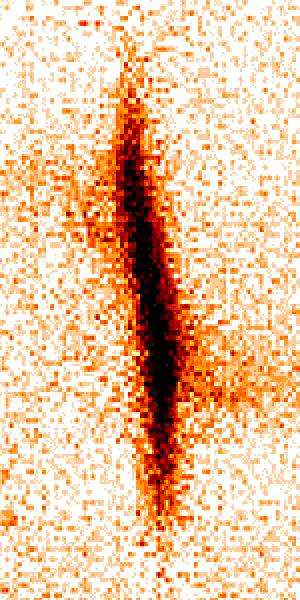
Bruit de fond
Crédit :
ESO
Signaux parasites et bruits
Au signal scientifique se superposent des signaux parasites et des bruits.
Un bruit sera caractérisé par son caractère aléatoire, et les propriétés statistiques correspondantes.
Un signal parasite possède, comme son nom l'indique, les propriétés d'un signal et non celles d'un bruit.
Bruit quantique
La nature du rayonnement, quantique par excellence, montre le hiatus à décrire une intensité lumineuse par une quantité analogique, alors que les porteurs de ce rayonnement sont quantifiés.
On montre que la
statistique d'arrivée des photons est poissonnienne.
Lorsque l'on attend 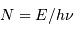 photons, la valeur moyenne
observée est
photons, la valeur moyenne
observée est 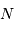 et la fluctuation
et la fluctuation 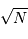 autour de cette
valeur moyenne. Il s'ensuit un rapport signal à bruit déterminé
par le flux de photons égal à :
autour de cette
valeur moyenne. Il s'ensuit un rapport signal à bruit déterminé
par le flux de photons égal à :
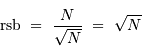
En électronique, on parle de bruit de grenaille, et de bruit de
photons en optique.
Bruit de fond
Le bruit de fond représente le bruit de photons de la lumière parasite qui se superpose au signal scientifique. Comme le bruit quantique, il est lié aux sources (ici parasites) et non au détecteur. Dans l'infrarouge, il est dominé par l'environnement chaud que voit le détecteur.
Bruit thermique
Le bruit thermique provient de l'agitation thermique des porteurs de charge du détecteur. Il est à moyenne nulle, son écart-type augmente avec la température.
Ce bruit, comme les suivants, dépend du détecteur et de la chaîne de détection.
Bruit de lecture
Le processus de lecture contribue au bruit de lecture, par exemple dans un CCD lorsque les photo-électrons sont transférés le long d'une colonne vers un registre de lecture.
On quantifie le bruit de lecture par son écart-type en nombre de photoélectrons par pixel. Une valeur typique de 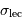 est de l'ordre de quelques photo-électrons par pixel
est de l'ordre de quelques photo-électrons par pixel
Bruit d'amplification
L'électronique d'amplification introduit un gain 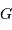 , dont la valeur n'est pas fixe mais sujette à différents bruits.
, dont la valeur n'est pas fixe mais sujette à différents bruits.
 Numérisation
Numérisation
Difficulté : ☆
Temps : 15 min
On souhaite numériser le signal photométrique d'un détecteur dédié à une étude de la microvariabilité. Ce signal est composé d'un fort continu, de diverses modulations et bruit, et du signal scientifique. Les amplitudes respectives sont données dans le tableau ci-dessous.
| continu | 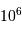 |
| variations | 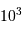 |
| microvariabilité | 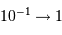 |
Question 1)
Sans traitement préalable, sur combien de bits faut-il coder le signal afin de ne pas introduire de bruit lors de cette opération (si besoin, voir les pages sur
l'échantillonnage d'un signal) ?
L'échantillonnage du signal requiert de coder le niveau de signal à la moitié de la plus petite variation.
Déterminer l'amplitude relative du signal entre le niveau de codage et la valeur maximale
Question 2)
Même question, après filtrage permettant de séparer les composantes continue et lentement variable d'une part, et la microvariabilité se distinguant du fond variable de l'autre.
Même démarche que précédemment.

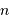 bits, ce qui permet de coder
bits, ce qui permet de coder 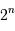 valeurs), peut rajouter du bruit au signal.
valeurs), peut rajouter du bruit au signal.


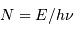 photons, la valeur moyenne
observée est
photons, la valeur moyenne
observée est 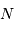 et la fluctuation
et la fluctuation 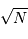 autour de cette
valeur moyenne. Il s'ensuit un rapport signal à bruit déterminé
par le flux de photons égal à :
autour de cette
valeur moyenne. Il s'ensuit un rapport signal à bruit déterminé
par le flux de photons égal à :
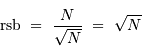
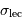 est de l'ordre de quelques photo-électrons par pixel
est de l'ordre de quelques photo-électrons par pixel
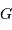 , dont la valeur n'est pas fixe mais sujette à différents bruits.
, dont la valeur n'est pas fixe mais sujette à différents bruits.
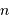 éléments d'information (bit), ce qui permet uniquement
éléments d'information (bit), ce qui permet uniquement 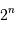 valeurs de codage.
valeurs de codage.
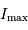 présentera, de par le codage sur
présentera, de par le codage sur 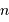 éléments d'information, une résolution minimale de
éléments d'information, une résolution minimale de 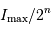 .
.
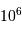
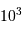
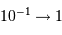
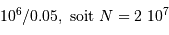 .
.