Grandeurs des éclipses de Lune

Nous avons vu que la taille des cônes d'ombre et de pénombre dépend de deux paramètres, la distance Soleil-Terre qui conditionne la position des sommets des cônes et la distance Terre-Lune qui conditionne la position du plan d'intersection des cônes.

Les éclipses les plus longues seront des éclipses centrales, la durée de l'éclipse est fonction de la vitesse synodique de la Lune, c'est à dire de la différence des vitesses entre la Lune et les cônes d'ombre et de pénombre car la Lune et les cônes d'ombre et de pénombre se déplacent dans le même sens par rapport à la Terre (sens direct). Le tableau suivant donne les valeurs extrêmes du demi-diamètre apparent (ρ) du cône d'ombre en tenant compte des corrections de réfraction. Pour ces valeurs on donne également les positions de la Terre et de la Lune, la valeur du demi-diamètre apparent de la pénombre (σ), la vitesse synodique de la Lune en secondes de degré par heure, la grandeur de l'éclipse et la durée totale de l'éclipse.

Demi-diamètre de l'ombre	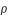Minimal : 2,61sL	Moyen : 2,69 sL	Maximal 2,78 sL
Positions de la Lune et de la Terre	Lune apogée - Terre périhélie	---	Lune périgée - Terre aphélie
Demi-diamètre de la pénombre	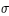4253" = 4,82 sL	4425" = 4,75 sL	4678" = 4,65 sL
Vitesse synodique de la Lune	1626"/h	1858"/h	2150"/h
Grandeur de l'éclipse	1,805	1,845	1,890
Durée de l'éclipse	environ 6h 19m	environ 5h 46m	environ 5h 17m

La grandeur maximale s'observe dans le cas des éclipses centrales périgées (avec la Terre à l'aphélie), mais la durée maximale s'observe pour les éclipses apogées (avec la Terre au périhélie) ; en effet dans ce cas le diamètre apparent de la Lune est plus petit mais son mouvement synodique est plus lent. On retrouve donc la dualité déjà observée dans le cas des éclipses de Soleil de durée maximale (éclipses annulaires à l'apogée) et les éclipses de Soleil de grandeur maximale (éclipses totales au périgée).