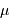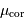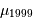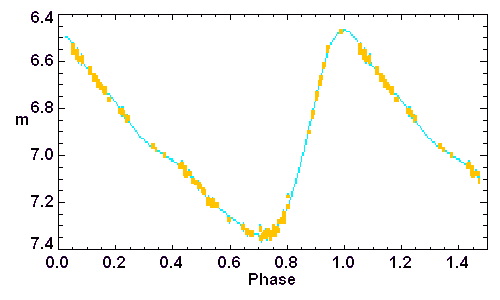
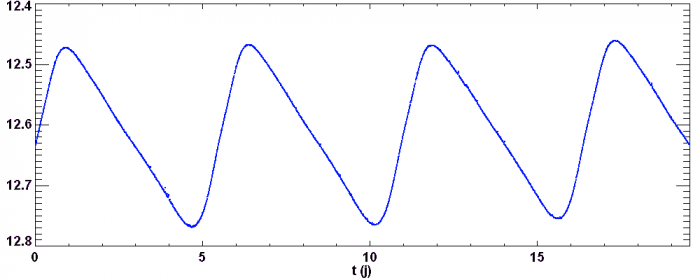
Courbe de lumière de l'étoile delta de la constellation de Céphée.
Crédit :
ASM
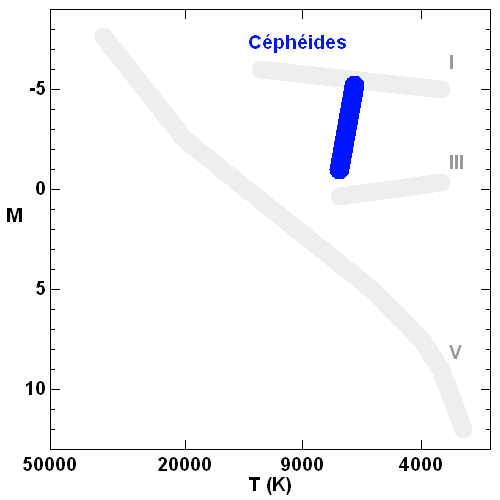
Les céphéides dans la bande d'instabilité du diagramme HR.
Crédit :
HST

Variabilité d'une céphéide dans la galaxie M100. Les trois petites images représentent la céphéide à des dates différentes.
Crédit :
HST
Courbe de lumière d'une céphéide observée par le satellite CoRoT.
Crédit :
CoRoT/CNES
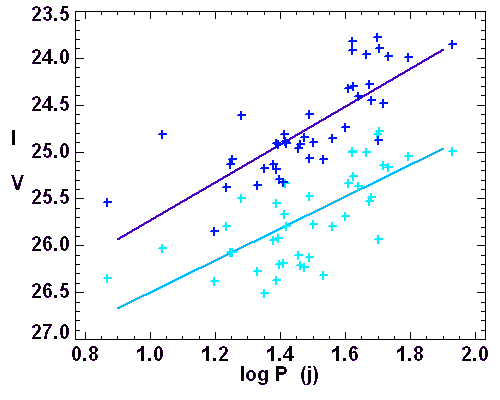
Relation entre période et magnitude apparente en bande V et I
Crédit :
ASM
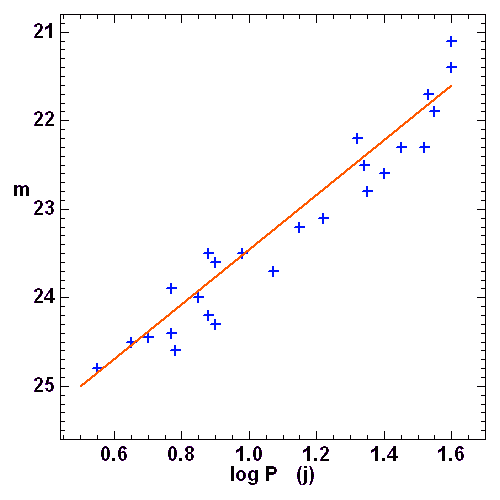
Relation entre la magnitude apparente et la période de céphéides d'une galaxie lointaine.
Crédit :
ASM
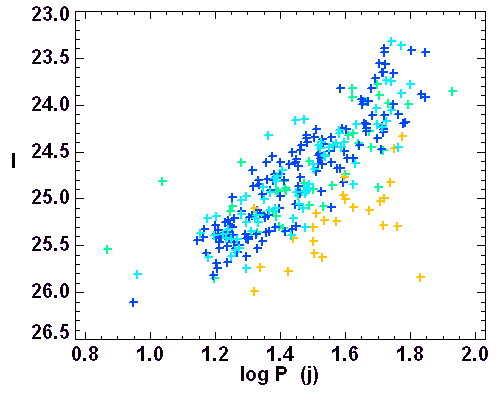
Diagramme période-luminosité pour les céphéides de quatre galaxies de l'amas de la Vierge. Chaque couleur correspond à une galaxie. Les croix oranges correspondent aux céphéides de la galaxie NGC4639. Les céphéides de cette galaxie, située en arrière plan de l'amas contrairement aux autres situées sur le front avant, voient leurs magnitudes augmentées d'une forte absorption.
Crédit :
ASM
Les céphéides, étoiles variables
Les céphéides, du nom de l'étoile 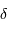 de la constellation de Céphée, sont de véritables phares : leur éclat , modulé, porte loin, si bien que leurs variations sont observables dans des galaxies à grande distance.
de la constellation de Céphée, sont de véritables phares : leur éclat , modulé, porte loin, si bien que leurs variations sont observables dans des galaxies à grande distance.
Les céphéides dans le diagramme HR
Les céphéides occupent une position particulière dans la bande d'instabilité
du diagramme HR.
La courbe de lumière de delta Céphée
La courbe de lumière d'un céphéide retranscrit sa pulsation radiale.
Relation période-luminosité
La magnitude absolue des étoiles variables céphéides varie linéairement avec le logarithme de leur période. Cet étalonnage permet de mesurer la distance d'objets plus lointains, pour lesquels on mesure les périodes et magnitude apparente.
Les céphéides et la distance de l'amas Virgo
On donne sur la figure le résultat des mesures de magnitude apparente et de période obtenues à partir des courbes de lumières de céphéides de quatre galaxies sélectionnées dans l'amas de galaxies de la Vierge (amas Virgo): NGC4321, NGC4496A, NGC4639 et NGC4536. Parmi elles, la galaxie NGC4639 fut en particulier observée parce que l'on y a observé une supernova de type Ia.
 Objectifs
Objectifs
Identifier un objet via une propriété caractéristique peut permettre la détermination de sa magnitude absolue, et donc de sa distance.
Les céphéides
Les étoiles céphéides sont des étoiles pulsantes dont la luminosité varie
périodiquement au cours du temps. Elles tiennent leur nom de l'étoile 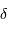 Céphée, identifiée en 1784 par John Goodricke.
Céphée, identifiée en 1784 par John Goodricke.
En étudiant les céphéides du Petit Nuage de Magellan, Henrietta Leavitt découvrit en 1912 que la période de variation de
leur éclat apparent est corrélée à leur magnitude absolue moyenne.
Les étoiles du Petit Nuage de Magellan étant toutes à la même distance de nous, leur éclat apparent (magnitude apparente 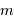 ) est donc un indicateur de leur luminosité intrinsèque (magnitude absolue
) est donc un indicateur de leur luminosité intrinsèque (magnitude absolue 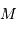 ) par la relation :
) par la relation :
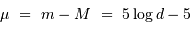
où la distance est exprimée en parsec.
L'étalonnage absolu de la relation période - luminosité
La relation énoncée par H. Leavitt est de la forme :
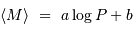
avec 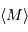 la valeur moyenne de la magnitude absolue et
la valeur moyenne de la magnitude absolue et 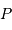 la période.
Comme le coefficient
la période.
Comme le coefficient 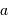 est négatif, plus une céphéide est lumineuse, plus
sa période est longue. Pour les céphéides de type I,
est négatif, plus une céphéide est lumineuse, plus
sa période est longue. Pour les céphéides de type I, 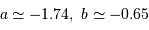 .
.
La relation admise aujourd'hui s'exprime avec les coefficients suivants, pour diverses bandes (B, V, I) :
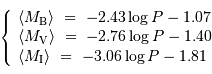
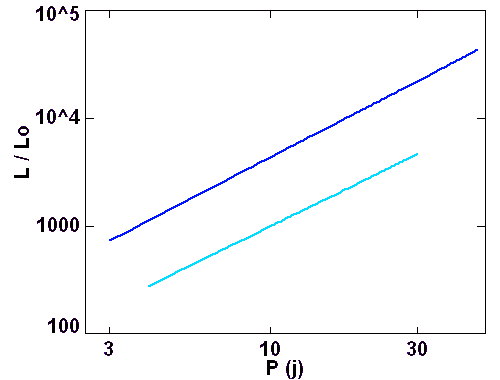
Relation période-luminosité pour les variables Céphéides (type I, bleu foncé ; type II, bleu clair).
Crédit :
ASM
Cette relation constitue bien un indicateur de distance puisque la mesure de la
période 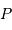 permet de déterminer
permet de déterminer 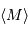 et donc la distance par comparaison avec la magnitude apparente médiane. La pente de la relation
pouvait être établie avec les céphéides du Petit Nuage de Magellan, mais la
détermination du coefficient
et donc la distance par comparaison avec la magnitude apparente médiane. La pente de la relation
pouvait être établie avec les céphéides du Petit Nuage de Magellan, mais la
détermination du coefficient 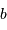 , qui fixe le point zéro de la relation nécessite un étalonnage avec des céphéides de distances connues. Cet étalonnage fut réalisé par E. Hertzsprung en 1913, puis par H. Shapley en 1918 en utilisant une
population de céphéides observées dans des amas globulaires de notre Galaxie.
Quand, en 1924, Edwin Hubble mesure pour la première fois des céphéides dans
M31, puis M33 et NGC6822, il utilisa cet étalonnage pour déterminer leurs
distances.
, qui fixe le point zéro de la relation nécessite un étalonnage avec des céphéides de distances connues. Cet étalonnage fut réalisé par E. Hertzsprung en 1913, puis par H. Shapley en 1918 en utilisant une
population de céphéides observées dans des amas globulaires de notre Galaxie.
Quand, en 1924, Edwin Hubble mesure pour la première fois des céphéides dans
M31, puis M33 et NGC6822, il utilisa cet étalonnage pour déterminer leurs
distances.
Les caractéristiques des Céphéides
| Type 1 | Type 2 |
| Type | F - G | F-G |
| Classe | Ia | Ia |
| période | de 3 à 50 j | de 5 à 30 j |
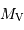 | de -2 à -6 | de 0 à -2 |
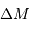 | de 0 à -6 | de 0 à -4 |
Les distances mesurables
Les céphéides ont l'avantage d'être intrinsèquement très
lumineuses et donc de pouvoir être observées à grande distance (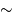 25 Mpc avec le télescope spatial Hubble). Leur mécanisme de pulsation est de plus physiquement bien connu, ce qui en fait un indicateur de distance très fiable. Ces étoiles sont observables essentiellement dans les galaxies spirales ou irrégulières, où il existe des populations stellaires jeunes.
25 Mpc avec le télescope spatial Hubble). Leur mécanisme de pulsation est de plus physiquement bien connu, ce qui en fait un indicateur de distance très fiable. Ces étoiles sont observables essentiellement dans les galaxies spirales ou irrégulières, où il existe des populations stellaires jeunes.
Le mécanisme des céphéides
Les céphéides sont des étoiles en phase de combustion centrale de l'hélium.
Lorsque l'étoile entre dans la phase d'instabilité, ses couches externes sont soumises à de légères variations de pression. Une compression conduit à l'ionisation du gaz, en particulier l'hélium présent proche de la surface. Or l'hélium ionisé est très opaque au rayonnement et agit donc comme un écran, qui, poussé par la pression de radiation, fait gonfler l'enveloppe de l'étoile comme un ballon.
La luminosité de l'étoile est fonction à la fois de sa température
superficielle et de son rayon d'après la loi de rayonnement du corps
noir. Quand l'enveloppe enfle, la surface émettrice
augmente. En se détendant, l'enveloppe se refroidit et les ions
d'hélium se recombinent avec les électrons. L'atmosphère redevient
alors perméable aux photons et retombe vers l'étoile.
L'accroissement du rayon et la baisse de température induisent des
effets opposés pour ce qui est de la luminosité. En pratique, les
variations de rayon et température sont en quadrature, et la
luminosité est en phase avec la température.
La durée de vie d'une céphéide dans cet état d'oscillation est de l'ordre de un million d'années. La plupart des étoiles entre 3 et 15 masses solaires passent par cette phase. Les étoiles les plus massives ont les périodes les plus longues : ayant un rayon plus important, elles mettent plus de temps à se dilater.
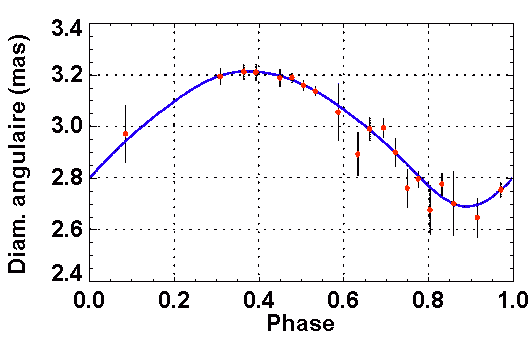
Mesure du diamètre d'une céphéide par interférométrie.
Crédit :
ASM
La relation Période-Luminosité d'un échantillon de céphéides
A l'aide de l'appliquette ci-dessous, déterminer la relation période-luminosité d'un échantillon de céphéides de notre galaxie.
- Représenter la relation période-luminosité.
- Estimer, à l'aide de l'appliquette, la pente et l'ordonnée à l'origine de la relation entre la magnitude absolue et le logarithme de la période exprimée en jour.
- Une céphéide présente une période de 13 jours, pour une magnitude apparente visible
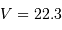 . En déduire sa distance.
. En déduire sa distance.

Solution :

Crédit :
ASM
 Les distances dans le Groupe Local par les céphéides
Les distances dans le Groupe Local par les céphéides
Difficulté : ☆☆
Temps : 1 h
On se propose d'estimer les distances des galaxies M31, M33 et NGC 6822 à partir des observations de Hubble de 1923-1928 et de la relation période-luminosité des céphéides établie pour le Petit Nuage de Magellan.
On dispose de courbes de lumière d'étoiles variables céphéides observées par Hubble entre 1923 et 1928 pour la nébuleuse d'Andromède M31, ainsi que pour M33 et NGC 6822. Ces données sont extraites de
trois articles de Hubble dans les "Contributions from the Mount Wilson Observatory" publiés en
1924, 1926, et 1929. Les magnitudes utilisées par Hubble sont des
magnitudes photographiques mesurées sur des photographies obtenues au foyer des télescopes de 1.52 m et 2.54 m du Mont Wilson. Ces magnitudes photographiques sont proches de celles du filtre bleu (B) utilisées plus tard dans le système photométrique UBVRI .
On dispose par ailleurs de courbes de lumières de céphéides du Petit Nuage de Magellan mesurées en magnitudes B et V par Halton Arp en 1955 et 1956, ainsi que d'une formule de correction pour remettre ces magnitudes dans le système
des magnitudes photographiques de Harvard qu'utilisait Harlow Shapley en 1918.
Dans ce système de magnitude, la relation période-luminosité des céphéides de Henrietta Leavitt (1912)
s'exprime comme suit :
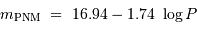
où 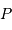 est la période mesurée en jour.
est la période mesurée en jour.

Question 1)
On donne dans la table les magnitudes médianes en bande B et les périodes des
courbes de lumière des céphéides du Petit Nuage de Magellan. Convertir ces magnitudes dans
le système des magnitudes photographiques de Harvard, à l'aide de la relation de conversion :
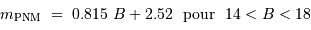
Calculer le logarithme de la période, donnée en jours.
Sélectionner la case B1, et entrer dans la ligne de commande = 0.815 * B +2.52
Sélectionner la case E1, et entrer dans la ligne de commande = log(P)
Question 2)
Mesurer la pente de la relation période-luminosité obtenue. Identifier et éliminer les points qui s'écartent de la distribution. Commenter et comparer le résultat à celui de Henrietta Leavitt.
Identifier les 2 points qui s'écartent de la distribution, et les éliminer en remplaçant leur magnitude par un tiret avant de procéder à l'ajustement.
Question 3)
Le point zéro absolu (ordonnée à l'origine) de la relation période-luminosité calibrée par H. Shapley en 1918 à partir des céphéides observées dans divers amas globulaires dont il connaît la distance par les RR-Lyrae est égal à -0.65.
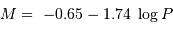
Calculer le module
de distance 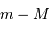 et la distance en années de lumière du Petit Nuage de Magellan.
et la distance en années de lumière du Petit Nuage de Magellan.
Se servir encore de l'appliquette, pour identifier l'ordonnée à l'origine lorsque l'estimation a une pente forcée à -1.74.
Question 4)
A période égale, les céphéides des galaxies M31, M33, et NGC6822 présentent des
magnitudes apparentes respectivement 5.90, 5.90 et 5.65 magnitudes moins brillantes. En déduire leur distance.
Se servir, encore, du module de distance.
Question 5)
A l'époque de Hubble, on ne connaissait pas encore les effets de l'extinction interstellaire, découverts par Trumpler quelques années plus tard.
Le tableau donne les valeurs de l'extinction galactique et extinction interne moyenne pour diverses galaxies, ainsi que les valeurs admises actuellement pour leur module de distance. Corriger le module distance des extinctions galactiques et internes, et comparer à la valeur admise aujourd'hui 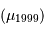 .
.
| Nom | ext. galactique | ext. interne | 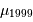 |
| PNM | 0.37 | 0.35 | 18.70 |
| M31 | 0.41 | 0.70 | 24.45 |
| M33 | 0.32 | 0.38 | 24.60 |
| NGC 6822 | 0.86 | 0.09 | 23.50 |
Comment joue l'absorption sur le module de distance du Petit Nuage de Magellan ?
 La distance de l'amas de la Vierge et le télescope spatial Hubble
La distance de l'amas de la Vierge et le télescope spatial Hubble
Difficulté : ☆☆
Temps : 45 min
On se propose de calculer la distance de l'amas de galaxies de La Vierge en utilisant des mesures de céphéides obtenues avec le télescope spatial.
| Nom | 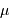 | site |
| NGC 4321 | 31.15 | HST |
| NGC 4496A | 31.13 | HST |
| NGC 4639 | 32.00 | HST |
| NGC 4536 | 31.10 | HST |
| NGC 4571 | 30.76 | Sol |
La table ci-jointe fournit, pour 5 galaxies attribuées à l'amas de La Vierge, les modules de distance déterminés par les céphéides, ainsi que la provenance de la mesure (HST ou terrestre). Par ailleurs, on connaît la valeur moyenne des vitesses radiales observées de l'amas :
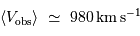
et la vitesse de chute de notre Groupe Local de galaxies en direction de l'amas de La Vierge :
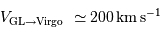
Question 1)
Déterminer la distance des objets de cet amas. Semble-t-il ramassé ou étendu ?
[3 points]
Question 2)
On cherche à déterminer la valeur moyenne de la distance de cet amas, qui présente une grande extension.
Montrer que l'identification des céphéides favorise la détection des composantes les plus proches. Quel biais cela peut-il introduire ?
[1 points]
Question 3)
Calculer la valeur moyenne de la distribution des distances.
[0.5 points]
Question 4)
En appliquant la loi de Hubble, déduire une estimation de la constante d'expansion de l'Univers 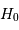 .
.
[1 points]
 Les globules dans la nébuleuse autour de la céphéide RS Pup
Les globules dans la nébuleuse autour de la céphéide RS Pup
Difficulté : ☆☆
Temps : 45 min
La céphéide RS Pup est entourée d'une nébuleuse circumstellaire,
qu'elle éclaire. Les courbes de lumières des globules dans cette
nébuleuse présentent la même périodicité que celle de la céphéide,
mais avec un retard dû à la propagation de la lumière de l'étoile
aux globules. Ce délai se traduit par un déphasage de leur courbe
de lumière. Les globules très proches du plan perpendiculaire à la
ligne de visée ont été sélectionnés : ils apparaissent sur les
"coquilles" de la nébuleuse entourant la céphéide. La période de
la céphéide, mesurée suite aux observations régulières sur la
céphéide, vaut P = 41.4389 j.
L'exercice se propose de reprendre les travaux d'un groupe
d'astronomes, principalement de l'Observatoire de Paris, qui ont
abouti à la mesure de la distance de cette étoile. Ces mesures
effectuées en 2007 constituent à ce jour la mesure de distance la
plus précise pour une céphéide.
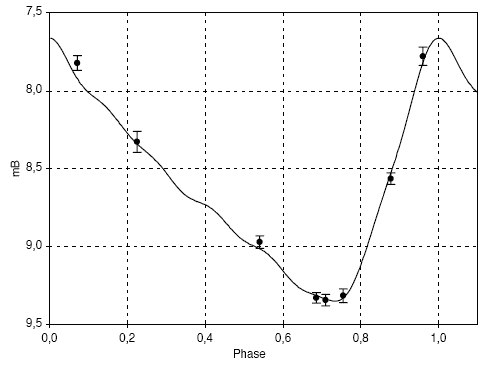
Courbe de lumière de la céphéide RS Pup. La phase est ici donnée en fraction de la période de variation.
Crédit :
ASM
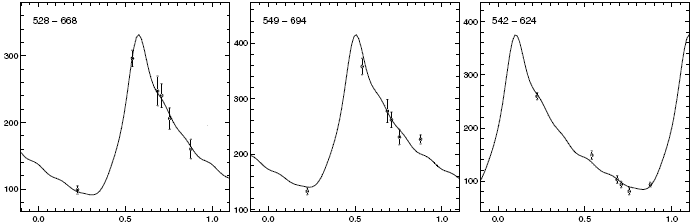
Mesures de la phase des courbes de lumière de 3 globules entourant RS Pup.
Crédit :
ASM

Question 1)
Montrer que la distance linéaire entre RS Pup et un globule
s'écrit : 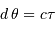 avec
avec 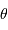 la distance
angulaire observée entre l'étoile et le globule, et
la distance
angulaire observée entre l'étoile et le globule, et 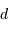 la
distance du système par rapport au Soleil. Pourquoi n'a-t-on
sélectionné que des globules dans le plan perpendiculaire à la
ligne de visée ?
la
distance du système par rapport au Soleil. Pourquoi n'a-t-on
sélectionné que des globules dans le plan perpendiculaire à la
ligne de visée ?
[2 points]
Il s'agit simplement d'exprimer de 2 façons différentes la distance linéaire entre l'étoile et le globule.
Question 3)
Montrer que la phase 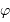 peut être mesurée, mais que le nombre entier
peut être mesurée, mais que le nombre entier 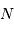 de périodes reste a priori inconnu.
de périodes reste a priori inconnu.
[1 points]
Quelle grandeur est observable ?
Question 4)
L'appliquette ci-jointe donne, pour les globules sélectionnés, les mesures de 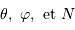 .
Le nombre
.
Le nombre 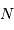 a été retrouvé par essai/erreur sur quelques valeurs.
Déduire alors de la nouvelle appliquette la distance
a été retrouvé par essai/erreur sur quelques valeurs.
Déduire alors de la nouvelle appliquette la distance 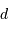 (en prenant soin d'éliminer l'une des mesures qui apparaît visiblement contradictoire avec les autres). Montrer qu'elle est directement donnée en parsec.
Est-elle compatible avec la valeur rapportée par les auteurs de ce travail :
(en prenant soin d'éliminer l'une des mesures qui apparaît visiblement contradictoire avec les autres). Montrer qu'elle est directement donnée en parsec.
Est-elle compatible avec la valeur rapportée par les auteurs de ce travail : 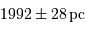 ?
?
[2 points]
Se servir de la relation trouvée entre les données et 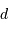 .
.
Le choix d'unité n'a pas été mené au hasard.
- Question 1
Aide :
S'aider du tableau.
Aide :
Sélectionner la case B1, et entrer dans la ligne de commande = 0.815 * B +2.52
Sélectionner la case E1, et entrer dans la ligne de commande = log(P)
Solution :
Les calculs indiqués donnent :
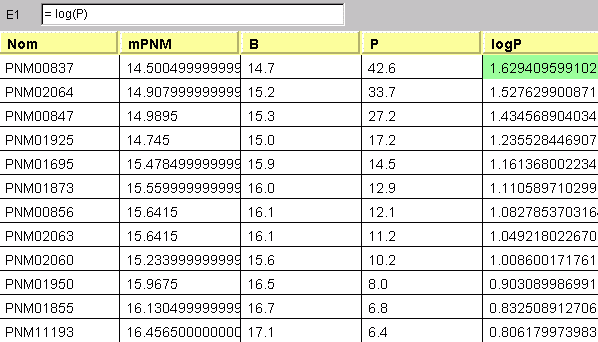
Crédit :
ASM
- Question 2
Aide :
Identifier les 2 points qui s'écartent de la distribution, et les éliminer en remplaçant leur magnitude par un tiret avant de procéder à l'ajustement.
Solution :
La plupart des céphéides du Petit Nuage de Magellan s'ajustent autour d'une droite de pente légèrement inférieure à 2. Deux des étoiles apparaissent sensiblement en dehors de la relation période-luminosité : PNM01925, PNM02060. Il est probable que cet écart provienne d'un mauvais étalonnage de leur magnitude.
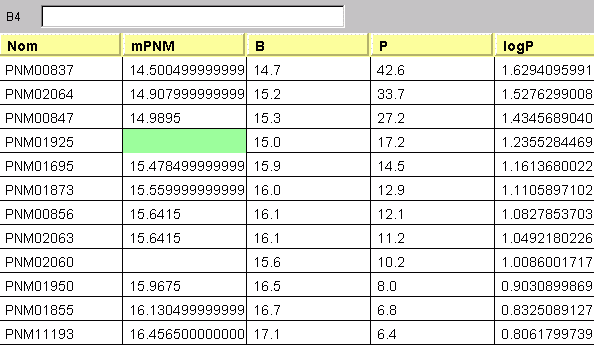
Exclusion des valeurs erronées.
Crédit :
ASM
Après exclusion de ces valeurs, l'estimation linéaire donne une pente de -2.03 et une ordonnée à l'origine de 17.9 ; la pente semble cohérente avec la pente de -1.74 de la relation de Henrietta Leavitt.
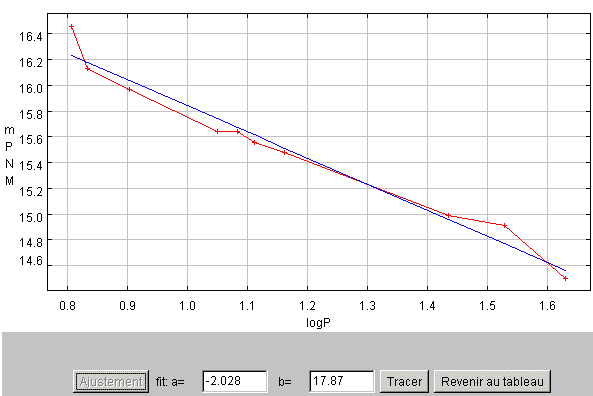
Estimation de la relation période-luminosité.
Crédit :
ASM
- Question 3
Aide :
Se servir encore de l'appliquette, pour identifier l'ordonnée à l'origine lorsque l'estimation a une pente forcée à -1.74.
Solution :
En forçant une pente de -1.74 on obtient pour le diagramme en magnitude apparente une ordonnées à l'origine de 17.5.
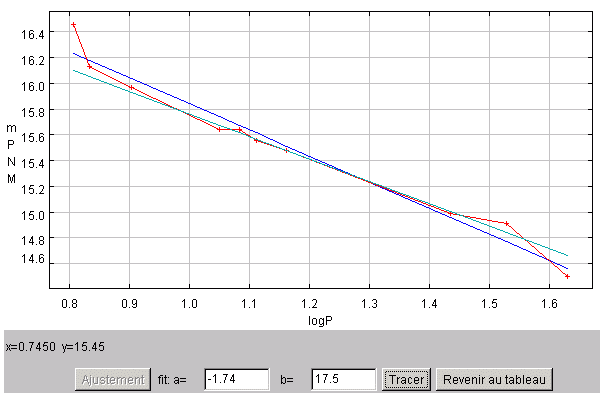
En rouge : les données ; en bleu : l'estimation linéaire de la relation période-luminosité ; en vert : l'estimation en forçant la pente
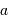
à -1.74, et en ajustant au mieux la valeur de l'ordonnée à l'origine
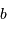
.
Crédit :
ASM
En soustrayant membre à membre les relations en magnitudes apparente et absolue, on trouve le module de distance du Petit Nuage de Magellan
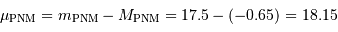
soit, d'après la définition du module de distance, une distance de 42.4 kpc (132 milliers d'années de lumière). En comparant aux dimension de la Voie Lactée  , on constate que le Petit Nuage de Magellan est tout proche de notre Galaxie. En fait, il en est l'un des proches satellites.
, on constate que le Petit Nuage de Magellan est tout proche de notre Galaxie. En fait, il en est l'un des proches satellites.
- Question 4
Aide :
Se servir, encore, du module de distance.
Solution :
D'après les données, les modules de distance de M31, M33 et NGC6822 sont respectivement de 24.05, 24.05 et 23.80, soit
des distances de 646, 646 et 575 kpc (2.0, 2.0 et 1.8 millions d'années de lumière).
En comparant à la dimension de la Voie Lactée, on voit que la distance de ces nébuleuses les place bien au-delà des limites de notre Galaxie. C'est cette découverte, couplée à la mesure de la taille de la Voie Lactée par H. Shapley, qui permit de clore le débat sur l'existence des univers îles et transforma notre univers d'étoiles et de nébuleuses en un univers de galaxies.
- Question 5
Aide :
Comment joue l'absorption sur le module de distance du Petit Nuage de Magellan ?
Solution :
Exprimé avec les mains : l'absorption ôte des photons, donc rajoute de la distance. Le module de distance est augmenté des effets de l'absorption dans notre Galaxie et interne à l'objet considéré.
L'absorption corrigeant à la hausse le module de distance du PNM de 0.72 magnitude, on trouve un module de 18.15+0.72 = 18.87, en bon accord avec la valeur admise aujourd'hui.
Pour les autres objets, repérés par rapport aux céphéides du PNM, il faut tenir compte de la correction différentielle par rapport au PNM.
On trouve finalement :
| Nom | ext. galactique | ext. interne | 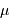 | 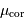 | 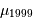 |
| PNM | 0.37 | 0.35 | 18.15 | 18.87 | 18.70 |
| M31 | 0.41 | 0.70 | 24.05 | 24.40 | 24.45 |
| M33 | 0.32 | 0.38 | 24.05 | 24.03 | 24.60 |
| NGC 6822 | 0.86 | 0.09 | 23.80 | 24.03 | 23.50 |
Ces résultats tenant compte de l'absorption sont en bien meilleur accord avec les valeurs admises aujourd'hui.






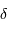 de la constellation de Céphée, sont de véritables phares : leur éclat , modulé, porte loin, si bien que leurs variations sont observables dans des galaxies à grande distance.
de la constellation de Céphée, sont de véritables phares : leur éclat , modulé, porte loin, si bien que leurs variations sont observables dans des galaxies à grande distance.

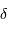 Céphée, identifiée en 1784 par John Goodricke.
Céphée, identifiée en 1784 par John Goodricke.
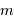 ) est donc un indicateur de leur luminosité intrinsèque (magnitude absolue
) est donc un indicateur de leur luminosité intrinsèque (magnitude absolue 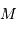 ) par la
) par la 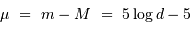
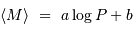
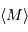 la valeur moyenne de la
la valeur moyenne de la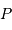 la période.
Comme le coefficient
la période.
Comme le coefficient 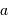 est négatif, plus une céphéide est lumineuse, plus
sa période est longue. Pour les céphéides de type I,
est négatif, plus une céphéide est lumineuse, plus
sa période est longue. Pour les céphéides de type I, 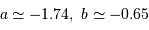 .
.
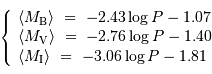

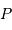 permet de déterminer
permet de déterminer 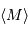 et donc la distance par comparaison avec la magnitude apparente médiane. La pente de la relation
pouvait être établie avec les céphéides du Petit Nuage de Magellan, mais la
détermination du coefficient
et donc la distance par comparaison avec la magnitude apparente médiane. La pente de la relation
pouvait être établie avec les céphéides du Petit Nuage de Magellan, mais la
détermination du coefficient 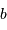 , qui fixe le point zéro de la relation nécessite un étalonnage avec des céphéides de distances connues. Cet étalonnage fut réalisé par E. Hertzsprung en 1913, puis par H. Shapley en 1918 en utilisant une
population de céphéides observées dans des amas globulaires de notre Galaxie.
Quand, en 1924, Edwin Hubble mesure pour la première fois des céphéides dans
M31, puis M33 et NGC6822, il utilisa cet étalonnage pour déterminer leurs
distances.
, qui fixe le point zéro de la relation nécessite un étalonnage avec des céphéides de distances connues. Cet étalonnage fut réalisé par E. Hertzsprung en 1913, puis par H. Shapley en 1918 en utilisant une
population de céphéides observées dans des amas globulaires de notre Galaxie.
Quand, en 1924, Edwin Hubble mesure pour la première fois des céphéides dans
M31, puis M33 et NGC6822, il utilisa cet étalonnage pour déterminer leurs
distances.
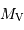
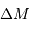
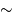 25 Mpc avec le télescope spatial Hubble). Leur mécanisme de pulsation est de plus physiquement bien connu, ce qui en fait un indicateur de distance très fiable. Ces étoiles sont observables essentiellement dans les galaxies spirales ou irrégulières, où il existe des populations stellaires jeunes.
25 Mpc avec le télescope spatial Hubble). Leur mécanisme de pulsation est de plus physiquement bien connu, ce qui en fait un indicateur de distance très fiable. Ces étoiles sont observables essentiellement dans les galaxies spirales ou irrégulières, où il existe des populations stellaires jeunes.

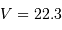 . En déduire sa distance.
. En déduire sa distance.

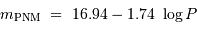
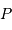 est la période mesurée en jour.
est la période mesurée en jour.
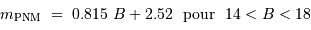
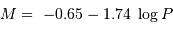
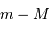 et la distance en années de lumière du Petit Nuage de Magellan.
et la distance en années de lumière du Petit Nuage de Magellan.
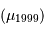 .
.
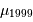
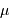
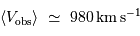
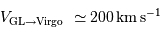
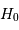 .
.


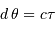 avec
avec 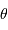 la distance
angulaire observée entre l'étoile et le globule, et
la distance
angulaire observée entre l'étoile et le globule, et 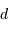 la
distance du système par rapport au Soleil. Pourquoi n'a-t-on
sélectionné que des globules dans le plan perpendiculaire à la
ligne de visée ?
la
distance du système par rapport au Soleil. Pourquoi n'a-t-on
sélectionné que des globules dans le plan perpendiculaire à la
ligne de visée ?
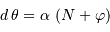 , avec
, avec 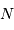 un entier et
un entier et 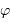 la phase du signal, exprimée en fraction de période. Exprimer le facteur
la phase du signal, exprimée en fraction de période. Exprimer le facteur 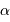 en fonction de la période
en fonction de la période 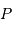 de la céphéide, puis le calculer pour une distance
de la céphéide, puis le calculer pour une distance 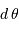 exprimée en UA.
exprimée en UA.
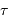 en fonction de la période et des données introduites.
en fonction de la période et des données introduites.
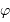 peut être mesurée, mais que le nombre entier
peut être mesurée, mais que le nombre entier 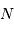 de périodes reste a priori inconnu.
de périodes reste a priori inconnu.
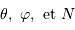 .
Le nombre
.
Le nombre 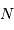 a été retrouvé par essai/erreur sur quelques valeurs.
Déduire alors de la nouvelle appliquette la distance
a été retrouvé par essai/erreur sur quelques valeurs.
Déduire alors de la nouvelle appliquette la distance 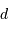 (en prenant soin d'éliminer l'une des mesures qui apparaît visiblement contradictoire avec les autres). Montrer qu'elle est directement donnée en parsec.
Est-elle compatible avec la valeur rapportée par les auteurs de ce travail :
(en prenant soin d'éliminer l'une des mesures qui apparaît visiblement contradictoire avec les autres). Montrer qu'elle est directement donnée en parsec.
Est-elle compatible avec la valeur rapportée par les auteurs de ce travail : 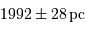 ?
?
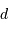 .
.




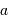 à -1.74, et en ajustant au mieux la valeur de l'ordonnée à l'origine
à -1.74, et en ajustant au mieux la valeur de l'ordonnée à l'origine 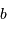 .
.
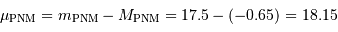
 , on constate que le Petit Nuage de Magellan est tout proche de notre Galaxie. En fait, il en est l'un des proches satellites.
, on constate que le Petit Nuage de Magellan est tout proche de notre Galaxie. En fait, il en est l'un des proches satellites.