
 Petite révision sur la formation d'image
Petite révision sur la formation d'image
Difficulté : ☆
Temps : 30 min
Un astronome extraterrestre regarde notre système solaire à une distance de 10 AL de notre Soleil. On souhaite dimensionner le télescope dont il aurait besoin pour distinguer Jupiter autour du Soleil.
On suppose le pouvoir de résolution de l'appareil limité par la seule diffraction : la tache de diffraction vaut angulairement 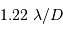 radian, où
radian, où 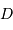 est le diamètre du télescope.
est le diamètre du télescope.
Pour la suite, on prendra 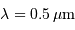 .
.
Question 1)
Déterminer la distance angulaire maximale 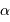 entre le soleil et Jupiter
entre le soleil et Jupiter 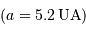 .
.
AideSolution
Rappel : 1 AL = 63 000 UA.
Question 2)
Déterminer 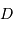 , le diamètre minimum du collecteur nécessaire.
, le diamètre minimum du collecteur nécessaire.
AideSolution
Un objet est résolu spatialement si sa taille angulaire est supérieure à la taille de la tache de diffraction.
Le diamètre minimum 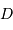 du collecteur est atteint lorsque la tache de diffraction est égale la distance angulaire maximum
du collecteur est atteint lorsque la tache de diffraction est égale la distance angulaire maximum 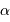 entre le soleil et Jupiter :
entre le soleil et Jupiter :
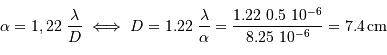
Pour tout télescope de diamètre supérieur, l'astronome extraterrestre peut résoudre Jupiter autour du Soleil.
Question 3)
Cela est-il suffisant?
AideSolution
S'intéresser au rapport des flux respectifs du Soleil et de Jupiter.
Le rapport des flux est tellement disproportionné qu'il faut un meilleur pouvoir séparateur de l'instrument ou une plus grande distance entre les 2 objets pour espérer voir la planète.

 Astrométrie
Astrométrie
Difficulté : ☆☆
Temps : 40 min
Le mouvement apparent d'une étoile voisine du soleil, corrigé de la parallaxe annuelle, est a priori rectiligne uniforme en l'absence de perturbation. On cherche à quantifier l'influence d'un compagnon planétaire.
On observe un système binaire composé d'une étoile de masse 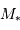 et d'une planète de masse
et d'une planète de masse 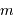 ( avec
( avec 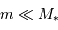 ) de rayon orbital
) de rayon orbital 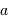 .
.
Question 1)
Justifier le caractère rectiligne et uniforme du mouvement stellaire, en l'absence de compagnon.
AideSolution
Un mouvement rectiligne uniforme est un mouvement non perturbé par quoi
que ce soit.
L'étoile observée est isolée, et donc elle obéit au principe de Galilée.
Question 2)
Exprimer l'amplitude de la perturbation angulaire maximale 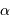 de la position de l'étoile, située à une distance
de la position de l'étoile, située à une distance 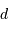 du Soleil.
du Soleil.
AideSolution
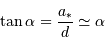
avec 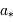 étant la distance du centre de l'étoile au centre de masse du système (étoile-planète)
étant la distance du centre de l'étoile au centre de masse du système (étoile-planète)
Question 3)
Retrouver l'expression :
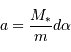
AideAideSolution
Définir le centre de masse.
Etablir 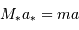
D'après la définition du barycentre 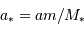 . Alors :
. Alors :
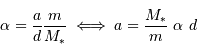
Question 4)
A quelle distance 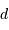 se situe l'étoile si sa parallaxe annuelle vaut 0.1" ?
se situe l'étoile si sa parallaxe annuelle vaut 0.1" ?
AideSolution
Le parsec est défini comme étant la distance d'une étoile ayant une parallaxe de 1".
Une étoile ayant une parallaxe de 0.1" est, par définition, à 10 pc.
Question 5)
Quelles planètes du système solaire, supposé vu à 10 pc, pourrait-on détecter, si l'on est capable de mesurer des variations de position à 0.01" ou 0.001" près ?
Compléter le diagramme ci-joint, positionnant les objets en fonction de leur masse 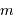 et de leur demi-grand axe
et de leur demi-grand axe 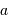 , en définissant la frontière qui marque la limite de détectabilité
(rappel
, en définissant la frontière qui marque la limite de détectabilité
(rappel 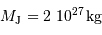 ).
).
Diagramme a-msin i
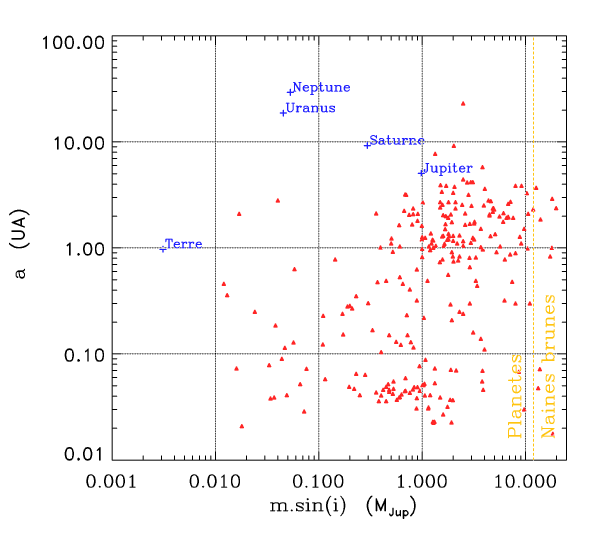
Crédit :
ASM
AideAideSolution
Traduire la relation établie précédemment entre 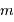 et
et 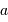 , et l'exprimer dans le système d'unités (UA, masse de Jupiter).
, et l'exprimer dans le système d'unités (UA, masse de Jupiter).
On traite l'équation :
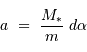
en tenant en compte que le produit 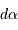 , avec
, avec 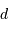 en pc et
en pc et 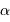 en " donne une distance en UA directement, par définition. En prenant
en " donne une distance en UA directement, par définition. En prenant 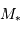 directement en masse jovienne (
directement en masse jovienne (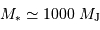 ), on obtient dans le système d'unités (UA,
), on obtient dans le système d'unités (UA, 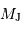 ), pour
), pour 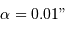 :
:
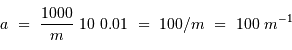
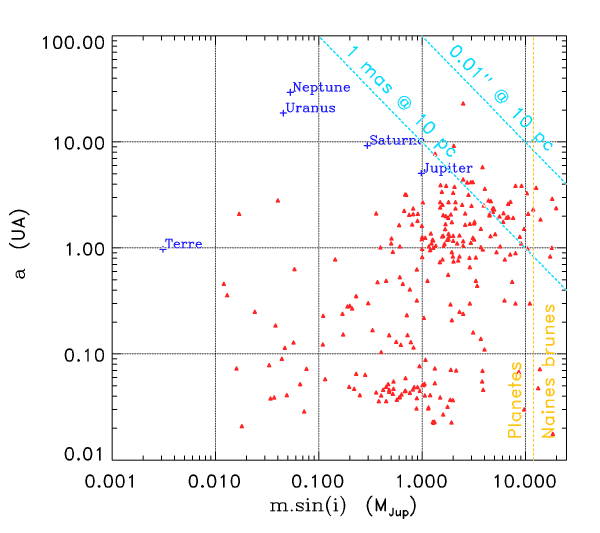
En échelle logarithmique, cette équation définit une droite de pente -1 ; elle passe par le point 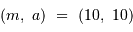 .
.
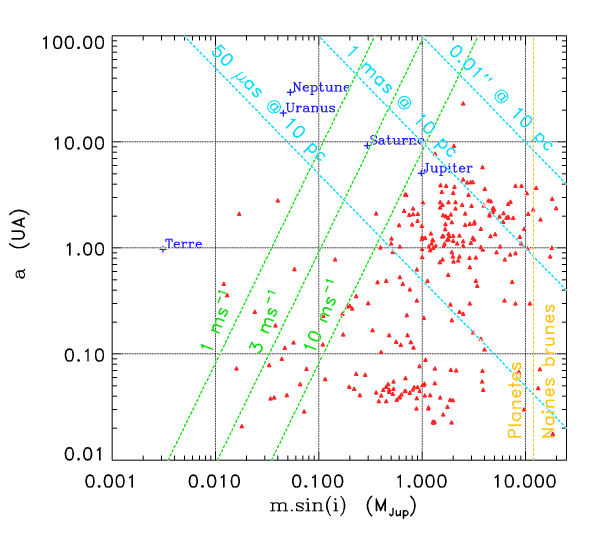
Pour une précision de 1 mas (1 millième de seconde d'arc), la courbe obtenue est définie par :
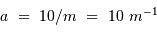
Parallèle à la précédente, elle contient le point
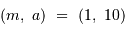 .
.
Comme le montre le diagramme ci-joint, aucune planète du système solaire n'est ainsi détectable à ce niveau de précision astrométrique.
Diagramme a-msin i
Crédit :
ASM
Question 6)
A terme, on imagine être capable de mesurer des écarts de position 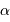 avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme
avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme 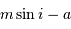 , pour un système à 10 pc et
, pour un système à 10 pc et 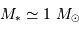 .
.
AideSolution
C'est la même chose que précédemment. Seule l'application numérique change.
Par rapport au cas précédent, le gain en précision d'un facteur 20 déplace la
limite vers les faibles masses, passant p.ex. par le point
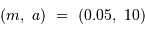 .
.
Planètes détectables
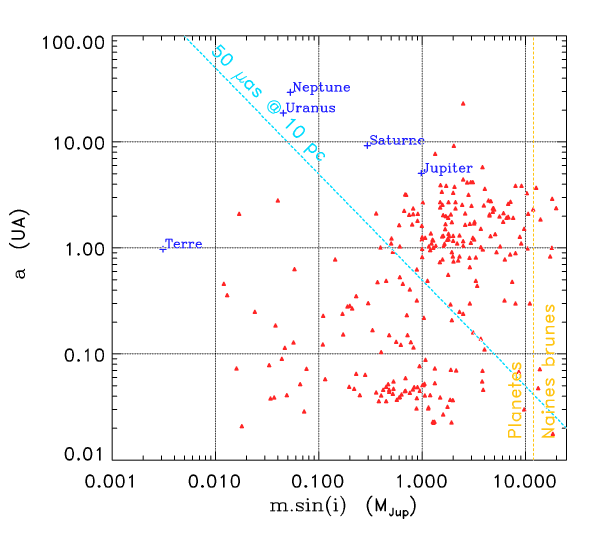
Crédit :
ASM
Question 7)
Quelles planètes du système solaire deviennent ainsi détectables ?
AideSolution
Si les graphes ont été dressés, la réponse n'est plus qu'une question de domaine.
Planètes détectables : Jupiter, Saturne, Uranus et Neptune. Seules les planètes géantes sont donc détectables, pas la Terre !
Planètes détectables
Crédit :
ASM

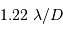 radian, où
radian, où 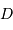 est le diamètre du télescope.
est le diamètre du télescope.
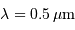 .
.
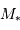 et d'une planète de masse
et d'une planète de masse 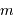 ( avec
( avec 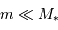 ) de rayon orbital
) de rayon orbital 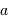 .
.
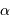 de la position de l'étoile, située à une distance
de la position de l'étoile, située à une distance 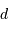 du Soleil.
du Soleil.
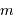 et de leur demi-grand axe
et de leur demi-grand axe 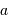 , en définissant la frontière qui marque la limite de détectabilité
(rappel
, en définissant la frontière qui marque la limite de détectabilité
(rappel 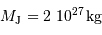 ).
).

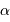 avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme
avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme 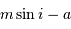 , pour un système à 10 pc et
, pour un système à 10 pc et 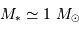 .
.